2.2. Контроль мінливості технологічного процесу

Розмахом називається різниця між максимальним і мінімальним значеннями вибірки.

( 2.3 )

Можлива і інша ситуація: середнє значення в нормі, але ми маємо суттєву різницю між окремими вимірюваннями, тобто процес нестабільний. Для контролю стабільності процесу використовують контрольні карти розмахів. За допомогою цих карт контролюється так званий розмах, тобто різниця між мінімальним і максимальним значенням у вибірці. Побудуємо контрольну карту розмахів для попереднього прикладу для чого скористаємося довідковими значеннями з таблиці 2.2.

Таблиця 2.2. Довідкові значення для розрахунку границь карти розмахів.

n	2	3	4	5	6	7	8	9	10	11
dn	1.128	1.163	2.059	2.326	2.534	2.704	2.847	2.97	3.078	3.173
rw	3.17	3.68	3.98	4.20	4.35	4.49	4.61	4.7	4.79	4.86
rλ	4.65	5.05	5.30	5.45	5.60	5.70	5.80	5.9	5.9	6.05

Центральна лінія проводиться на рівні

, ( 2.4 )

де n – об'єм вибірки, σ – стандартне відхилення;

Верхня попереджувальна границя відсікає 2,5% значень у верхній частині розподілу, тобто за умови нормального протікання процесу розмах вибірки перевищує дане значення в одному випадку з сорока

, ( 2.5 )

верхня границя регулювання відсікає 0,1% значень у верхній частині розподілу, тобто за умови нормального протікання процесу розмах вибірки перевищує дане значення в одному випадку з тисячі

, ( 2.6 )

Виконаємо розрахунки для розміру вибірки, що дорівнює 5, σ = 0,15, d_n = 2,326; r_w = 4,20; r_λ = 5,45, отже:

центральна лінія ;

верхня попереджувальна границя ;

верхня границя регулювання .

Обчислимо розмахи кожної вибірки.

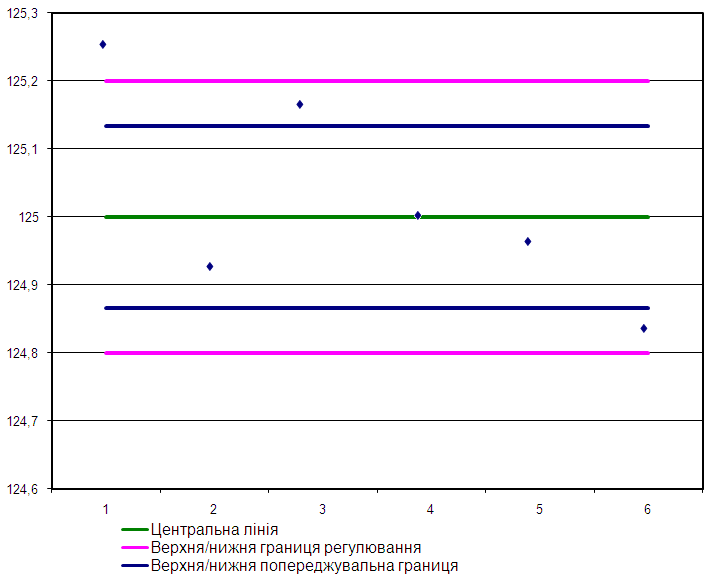
Рис. 2.1. Контрольна карта, для перевірки вибіркового середнього.

Таблиця 2.3. Приклад визначення розмахів.

Номер вибірки	1	2	3	4	5	6
Розмах вибірки	0.5	0.4	0.3	0.5	0.4	0.3

Всі значення розмахів нижче верхньої попереджувальної границі, отже можна вважати, що процес стабільний.

2.3. Побудова контрольних карт середнього значення

Для випадку, коли невідомі вага упаковки μ та стандартне відхилення σ, то в якості оцінки μ береться середнє всіх середніх індивідуальних значень. Для кожної вибірки вираховується , а потім – середнє всіх середніх . У випадку нашого прикладу . При невідомому значенні σ, його оцінку знаходимо наступним чином: визначаємо середнє значення всіх розмахів і з таблиці 2.2 беремо значення d_n =2,326. Потім із співвідношення 2.7 визначаємо

(2.7 )

Границя регулювання контрольної карти середнього розраховується за формулою

, (2.8 )

В даному випадку ця формула має вигляд

, ( 2.9 )

Верхня границя регулювання контрольної карти розмахів розраховується за формулою

(2.10 )

Оскільки величина 3/d_n√n є сталою величиною, то вона позначається як А і вираз для границь регулювання матиме вигляд

, (2.11)

Величина r_λ / d_n також являє собою константу, яку називають С, і тоді рівень верхньої границі регулювання розмахів дорівнює (С* ). Рівень нижньої границі регулювання розмахів визначається як (В* ). Значення А, В і С подані в табл. 2.4.

Таблиця 2.4. Довідкові значення констант для побудови карти розмахів.

Число спостережень в групах, n	A	B	C
2	1.88	0	3.27
3	1.02	0	2.57
4	0.73	0	2.28
5	0.58	0	2.11
6	0.48	0	2.00
7	0.42	0.08	1.92
8	0.37	0.14	1.86
9	0.34	0.18	1.82
10	0.31	0.22	1.78
20	0.18	0.41	1.59

Знайдемо границі регулювання для контрольної карти середнього значення.

Для n=5, A = 0.58,

.

Контрольна карта розмахів складається із центральної лінії та верхньої і нижньої границь регулювання для розглянутого прикладу має такий вигляд:

Центральна лінія:

Верхня границя регулювання С:

Нижня границя регулювання В: .

Висновок. Якщо середнє значення, певної вибірки виходить за межі означення попереджувальної границі, то це означає що наступне дослідження слід зробити через проміжок часу, який орієнтовно дорівнює ∆t/2.

Якщо середнє значення, певної вибірки виходить за лінію регулювання, то процес зупиняється і з’ясовуються та усуваються причини такого відхилення.