2.2. Практическая часть

2.2.1 Составьте программу имитационного моделирования движения автобуса для и -стратегий в соответствии с блок-схемой на рис. 2.4, отладьте и протестируйте ее.

Полезный совет. Прежде чем программировать предложенную блок-схему попытайтесь разделить ее на две отдельные, соответствующие разным стратегиям обслуживания.

2.2.2 Для анализа длительности прогонов модели на точность оценок, постройте на основе результатов моделирования графики зави­симостей среднего числа рейсов и для количества модели­руемых дней равном 1, 2, 3, 4, 5, 10, 20 и 90 дней. На этих же графиках укажите точное значение соответствующих средних значений и . Принять требуемое число рейсов в день равное 10 и = 0.4, = 0.7.

2.2.3 С помощью разработанной программы постройте параметриче­ские графики зависимостей среднего числа рейсов и от ве­роятности перехода , задав длительность моделирования 90 дней при требуемом числе рейсов в день равном 10. Для построения графиков рекомендуется задать следующее множество значений вероятностей

при значениях параметра

Сравните полученные зависимости с графиками точных значений соответствующих средних значений, полученными по формулам.

2.2.4 На графиках, построенных в предыдущем пункте, выделите облас­ти предпочтительного использования той или иной стратегии об­служивания.

2.2.5 Сделайте (письменно) выводы по работе, касающиеся рекоменда­ций по методике выбора той или иной стратегии обслуживания для различных параметров задачи.

3Лабораторная работа №3 исследование и оптимизация системы контроля

Целью данной работы является развитие навыков составления программы имитации элементарной системы массового обслуживания (СМО), ее эксплуатации на приме­ре некоторой системы контроля (СК).

Рекомендуемый порядок выполнения работы:

• помощью имитационной модели найти характеристики одноканальной СК;

• найти оптимальное число каналов СК, обеспечивающее требуемую веро­ятность обслуживания изделий;

• найти операционные характеристики оптимальной многоканальной СК.

3.1. Постановка задачи

Описание проблемной ситуации

Рассматривается следующий пример.

На выходе поточной линии готовые изделия проходят функциональный контроль на специальных однотипных стендах. Изделия сходят с конвей­ера в случайные интервалы времени, распределенные равномерно на ин­тервале мин.

Если все стенды к моменту поступления изделия на контроль оказыва­ются занятыми, то изделие остается непроверенным и в таком виде мо­жет поступить потребителю. При наличии хотя бы одного свободного стенда изделие подвергается контролю. Каждый из стендов одновремен­но может контролировать только одно изделие. Время контроля на лю­бом стенде случайное и распределено также равномерно на интервале мин.

Требуется определить количество контрольных стендов, которые необ­ходимо установить на выходе поточной линии, чтобы обеспечить кон­троль не менее готовых изделий.

Рассматриваемая система является дискретной, поскольку в ней события, проис­ходят в некоторые случайные моменты времени. Действительно, изделия, посту­пающие с поточной линии на контроль, образуют случайный входной поток заявок, а контрольные стенды являются каналами обслуживания данных заявок. После обслуживания, изделия не поступают на какую-либо последующую обработку, а об­разуют случайный выходной поток проконтролированных (обслуженных) изделий. Это означает, что СК является разомкнутой и однофазной.

Тот факт, что в случае занятости всех каналов заявка получает отказ, позволяет го­ворить о СК как о системе обслуживания с отказами, т.е. без очереди (или без ожидания). Источник заявок (поточная линия) может считаться неограниченным.

Таким образом, мы классифицировали СК как однофазную, разомкнутую, - канальную систему массового обслуживания (СМО) с отказами и дисциплиной об­служивания.

Цель исследования: найти такое число каналов , ко­торое обеспечит контроль всех изделий. Очевидно, что в терминах теории СМО это требование тождественно требованию обеспечения вероятности обслу­живания заявок .

Метод решения задачи оптимизации

Для того, чтобы найти требуемое (оптимальное) количество каналов, обеспечиваю­щее контроль изделий с вероятностью достаточно построить зависимости от числа каналов обслуживания (рис. 3.1).

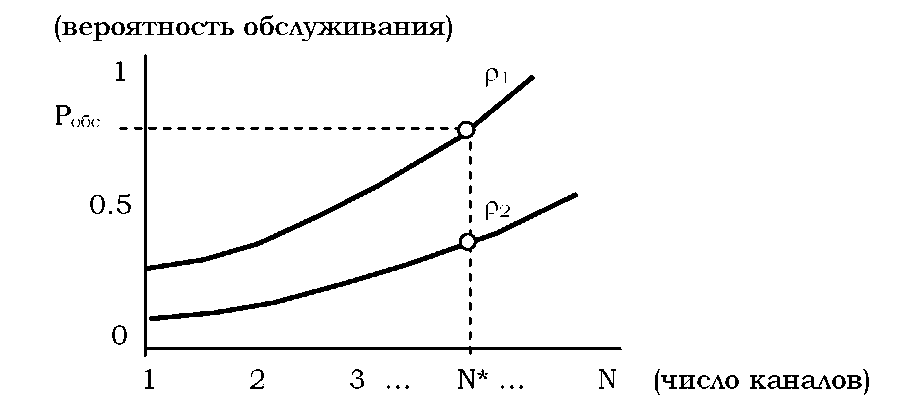
Рис. 3.1 Зависимость от числа каналов обслуживания для разных значений коэффициента нагрузки

Такие зависимости называются нагрузочными кривыми. Ясно теперь, что, зная ко­эффициент загрузки и требуемую вероятность обслуживания можно всегда определить искомое число каналов .

Очевидно, что вся проблема в задачах такого рода заключается в построении нагру­зочных характеристик исследуемой СМО. Нагрузочные характеристики для различ­ных СМО имеют разный характер. Они могут быть рассчитаны аналитически либо найдены с помощью имитационных моделей.

Поскольку входной поток рассматриваемой СК не экспоненциальный, то мы не мо­жем использовать уравнения Эрланга, и поэтому единственным способом анализа системы является имитационное моделирование.

Вместо явного построения нагрузочных характеристик в данной работе предлагается программный метод оценки требуемого числа каналов .

Для нахождения требуемого числа каналов предлагается воспользоваться мето­дом перебора. Это означает, что саму имитационную модель СК включают в опре­деленный внешний цикл программы. В этом цикле осуществляется моделирование и проверка условия обслуживания по вероятности для последовательного чис­ла каналов N от 1,2, ... до .

Блок - схема имитационной модели системы контроля

На первом этапе исследователю необходимо составить блок-схему имитационной модели.

Это сложный этап, от которого, как правило, зависит успех всего машинного экспе­римента. Поэтому в учебных целях в этой работе представлена уже подробная гото­вая блок-схема алгоритма моделирования и оптимизации СК (рис. 3.2).

Работа алгоритма не требует особых пояснений - она понятна из блок-схемы, а процесс поиска оптимального числа контрольных стендов, описанный выше, состоит в последовательном вычислении вероятности обслужи­вания для и нахождении оптимального значения . Поэтому только перечислим используемые в алгоритме основные идентификаторы и их функциональное назначение:

- начальное число контрольных стендов (обычно );

- текущее значение числа стендов;

- число отказов в обслуживании вначале равно 0;

- время обслуживания на одном -м стенде;

- текущее (модельное) время моделирования;

- объем источника контролируемых изделий (объем выборки);

- счетчик требований;

Tau1=F1(Rnd) - случайный интервал времени между приходами изделий на контроль, ге­нерируемый оператором F1 c помощью базовых случайных чисел Rnd;

Tau2=F2(Rnd) - случайное время контроля изделия стендом, генерируемый оператором F2 c помощью базовых случайных чисел Rnd;

- оценка вероятности отказа в контроле изделия; - требуемая вероятность от­каза контроля изделий.

Блок-схема представляет основную версию имитационной модели, и студент вправе не только вносить свои частные изменения, но и разработать собственный вариант блок-схемы.

Формализм имитационной модели системы контроля

Этот раздел поможет понять структуру имитационной модели, а также вспомнить теоретические аспекты машинного эксперимента, что необходимо при сдаче работы.

Данная имитационная модель СМО, по существу, заключается в моделировании случайных дискретных событий, которые последовательно возникают во время ра­боты реально существующей поточной линии и контрольных стендов. Здесь случай­ное событие определяется как точка во времени, в которой происходят изменения состояния, а значит и характеристик системы. Обычно эти скачкообразные измене­ния имеют место в тех случаях, когда кончается один процесс (или несколько про­цессов) и начинаются другие.

Поэтому, мы используем принцип имитации дискретных событий, который заключа­ется в том, что для получения требуемых результатов моделирования достаточно наблюдать систему в те моменты, когда в ней происходят случайные события.

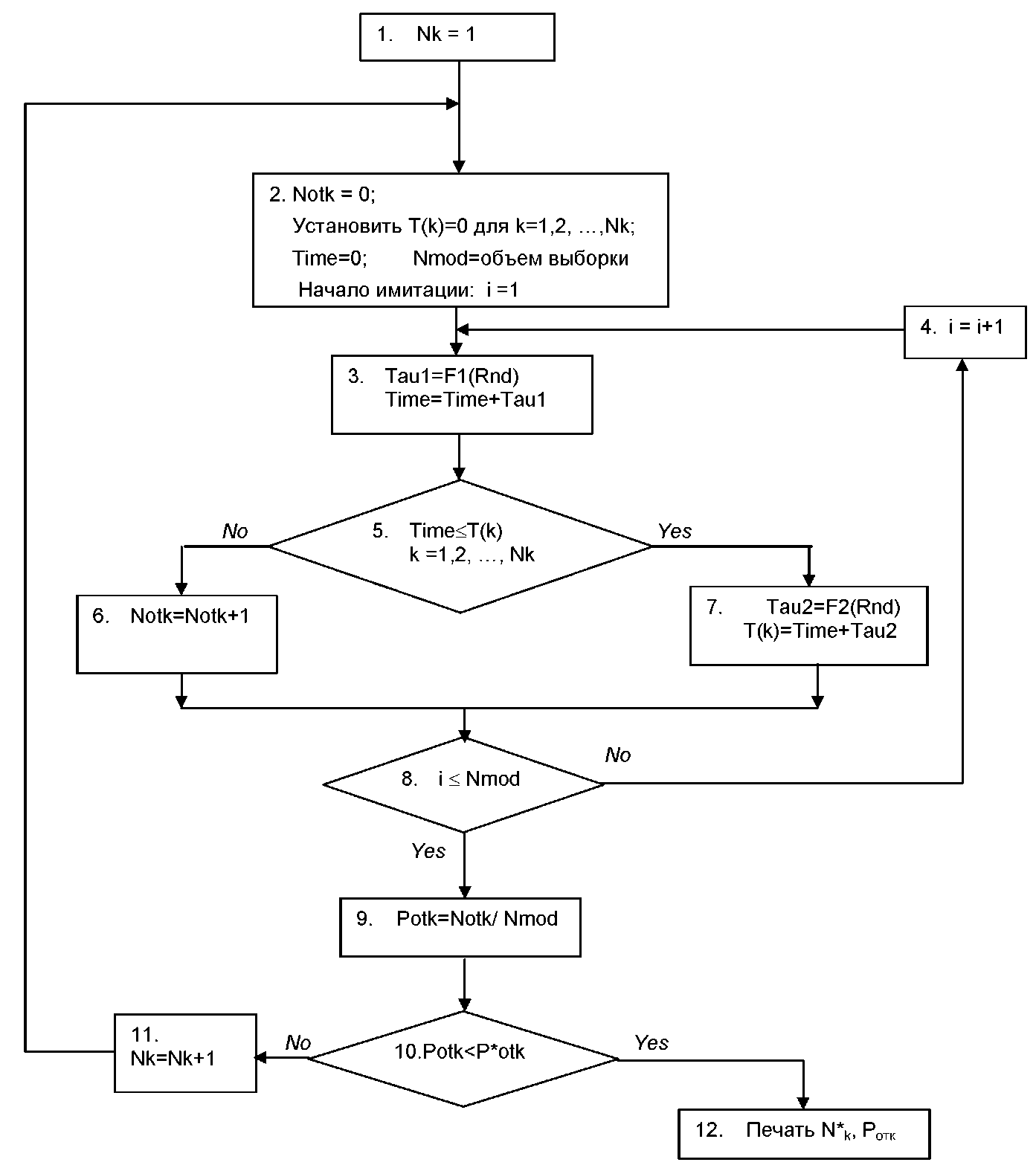
Рис. 3.2 Блок-схема алгоритма имитационной модели системы контроля

Например, для СК такая операционная характеристика как вероятность отказа изменяет свое значение либо в момент поступления очередного требования, либо в момент окончания обслуживания. Действительно заявке может быть отказано в об­служивании, или она станет на обслуживание.

Таким образом, модель функционирует как бы «прыгая» строго последовательно от одного события к другому. На рис. 3.3 показан типичный процесс работы дискретной имитационной модели. Каждое событие на шкале времени отмечено кружком.

Рис. 3.3 Процесс функционирования имитационной модели

В случае дискретного моделирования между реальным временем и временем рабо­ты модели нет ничего общего. Поскольку модель реализуется в виде переходов из одного состояния в другое, то промежутки между событиями фактически не модели­руются, и поэтому работу системы, например, за целый месяц можно промоделиро­вать за гораздо меньший промежуток времени.

При эксплуатации имитационной модели всегда нужно иметь ввиду, что, по сущест­ву, мы имеем дело с машинным экспериментом, результаты которого должны ин­терпретироваться на основе соответствующих статистических проверок.

Первая специфика таких экспериментов заключается в том, что результаты имита­ции достигают своих стационарных значений только после многократного (но неиз­вестного априори!) повторения эксперимента. Типичные статистические оценки ими­тационного моделирования одноканальной СМО Эрланга выглядят так, как на рис.4.

Обратите внимание, в частности, на то, что на рис. 3.4 мы оценивали вероятность от­каза, что не принципиально для обсуждаемого вопроса, т.к. .

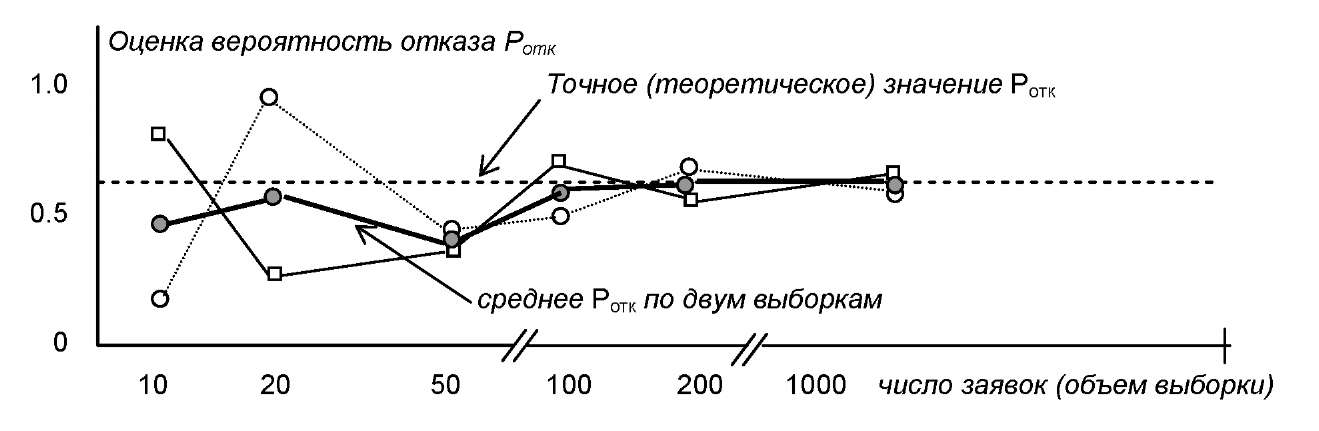
Рис. 3.4 Разброс оценок вероятности отказа в обслуживании и их средние значения для 2-х прогонов модели

Рассмотрим вначале какой-либо один из двух прогонов.

Мы видим, что в начале прогона (10-20 заявок) оценка колеблется весьма силь­но около точного значения (для СМО Эрланга существуют аналитические соотноше­ния). Затем, по мере увеличения длительности прогона оценка стабилизируется около точного значения. Это условие стабилизации оценки достигается обычно по­сле повторения эксперимента достаточное количество раз. На такой характер изме­нения оценок нужно ориентироваться и в этой работе.

Таким образом, для качественного имитационного моделирования необходимо ре­шать следующие вопросы:

• какова должна быть продолжительность прогона для достижения стацио­нарных условий?

• каким образом получать статистически независимые наблюдения?

• сколько наблюдений требуется для достижения необходимого значения до­верительных интервалов?

Однако, главной проблемой для разработчика имитационной модели была и остает­ся проблема тестирования модели. В связи с этим, студенту предлагается провес­ти тестирование на основе разработки имитационной программы системы Эрланга, имеющей аналитическое описание.

Т.е. вначале нужно:

• выбрать исходные данные в колонке «Тестовая СМО Эрланга»;

• рассчитать характеристики СМО Эрланга по известным формулам;

• разработать имитационную модель этой СМО и путем сравнения аналити­ческих и имитационных характеристик протестировать и отладить модель.

• в программу уже протестированной модели Эрланга внести необходимые изменения в части имитации равномерно распределенного входного потока и вре­мени обслуживания, и тем самым реализовать нужный вариант системы контроля.

Теперь можно приступить к выполнению практической части работы.

Найдите свой вариант исходных данных системы контроля из таблицы и выполните все пункты нижеследующего раздела «3.2 Практическая часть».

Варианты исходных данных системы контроля

Вариант №	Тестовая СМО Эрланга		Система контроля
	интенсивность потока (1/мин)	интенсивность обслуживания (1/мин)	параметры равномерного потока (мин)	параметры равномерного времени обсл (мин)
1	0.95	1.0	[5, 15]	[15, 25]
2	0.05	0.06	[6, 16]	[20, 30]
3	0.025	0.025	[5, 15]	[18, 34]
4	0.025	0.02	[1, 19]	[19, 35]
5	2.0	1.0	[5, 15]	[20, 30]
6	0.2	0.1	[6, 20]	[14, 34]
7	3.0	2.0	[1, 19]	[20, 30]
8	4.0	3.0	[8, 18]	[18, 28]
9	1.0	0.1	[6, 20]	[18, 28]
10	1.5	0.25	[1, 19]	[15, 25]