2Лабораторная работа №2 анализ вариантов обслуживания автобусов на основе имитационной модели

В данной практической работе рассматривается задача выбора наибо­лее рационального варианта технического обслуживания рейсовых ав­тобусов.

Инструментом анализа вариантов послужит имитационная модель «по­ведения» автобуса, которая должна быть разработана в рамках данной работы.

2.1. Постановка задачи

Рассмотрим описание задачи ситуации, с которой столкнулась админи­страция автобусного парка, скажем, в городе ADVANCED.

Каждый рейсовый автобус должен по плану делать ровно N рей­сов в день. Каждый день свой первый рейс автобус начинает в хорошем, т.е. в полностью исправном состоянии. Если автобус начинает определенный рейс в хорошем состоянии, то он имеет ненулевую вероятность того, закончит его в некотором «ухуд­шенном» состоянии.

«Ухудшенное» состояние автобуса характеризуется тем, что ав­тобус может продолжать свой путь, т.е. возникла некая неболь­шая неисправность. Известно, что ремонт такой небольшой не­исправности занял бы время одного рейса (можно сказать, что стоимость одного такого ремонта равна стоимости одного несо­стоявшегося рейса). Ремонт производится по окончании рейса, в котором случилась поломка и, как говорилось, занимает все вре­мя следующего рейса.

Если же автобус продолжает работу в «ухудшенном» состоянии (водитель отказался от ремонта, решив продолжать работу на линии с небольшой неисправностью автобуса), то вновь сущест­вует некоторая ненулевая вероятность того, что он может перей­ти в полностью нерабочее состояние, когда немедленно требует­ся ремонт, т.е. автобус становится «на прикол». Предполагается, что полностью неисправным автобус может стать только при на­личии мелкой неисправности.

Если автобус попал в это нерабочее состояние, то приходится отменить все оставшиеся на текущий день рейсы, т.к. автобус будет находится в ремонте до конца дня.

Также известно, что каждый новый день автобус начинает только в полностью исправном состоянии вне зависимости от того, в ка­ком состоянии он закончил рабочий день, поскольку, при необхо­димости, проводится ночной ремонт.

Администрация автопарка имеет возможность дать указания водителям автобусов строго придерживаться какого-либо одного из следующих двух правил (стратегий) по ремонту (обозначим их как а и в):

Правило - «производить ремонт небольших неисправно­стей на линии, т.е. сразу же, как только автобус переходит в «ухудшенное состояние»;

Правило - «не устранять небольшие неисправности на линии, т.е. эксплуатировать автобус до его пол­ной поломки».

Интуитивно администрация представляет, что среднее число рейсов, а значит и общие издержки должны зависеть от реализации того или иного правила эксплуатации

В связи с этим перед приглашенными аналитиками была поставлена следующая проблема:

определить такое правило эксплуатации автобуса из числа предложенных и , при котором обеспечивается максимум среднего числа рейсов в день.

Формулирование модели

Прежде чем приступать к решению необходимо попытаться формализо­вать задачу. Очевидно, что «поведение» любого рейсового автобуса в данной задаче можно представить конечным множеством следующих достаточно устойчивых состояний:

состояние 1: «автобус полностью исправен»;

состояние 2: «автобус в ухудшенном состоянии»;

состояние 3: «автобус полностью неисправен».

Обозначим для удобства состояния 2 и 3 буквами А и B, а вероятности переходов в состояние А и В буквами и соответственно.

Тогда по условиям задачи все возможные состояния и все возможные переходы между ними можно изобразить в виде некоторого графа пере­ходов (рис. 2.1).

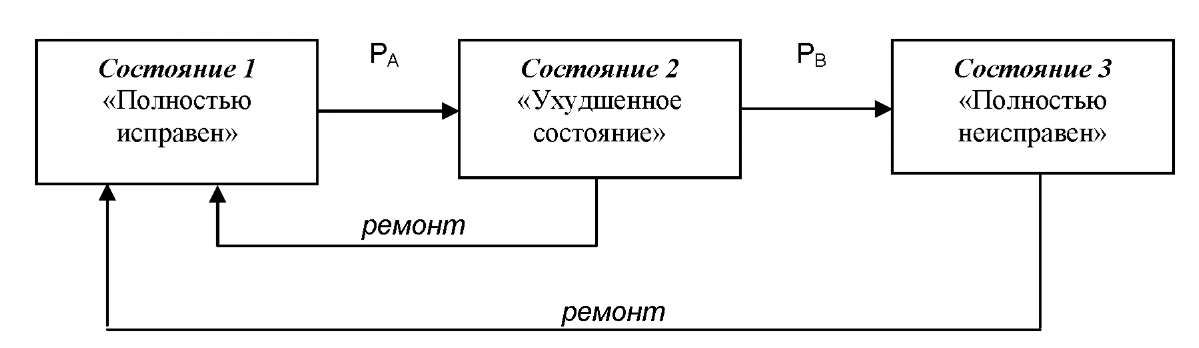
Рис. 2.1 Граф переходов состояний автобуса

Однако пока неясно, какое правило эксплуатации отражает этот граф переходов. Поэтому целесообразно более подробно проанализировать возможные ситуации, которые могут случиться с автобусом в течение рейса при различных правилах ремонта.

Докажите, (если вы согласны) что графы переходов, изображенные на рис. 2.2 и 2.3 соответствуют правилам ремонта (эксплуатационным полити­кам) а и р.

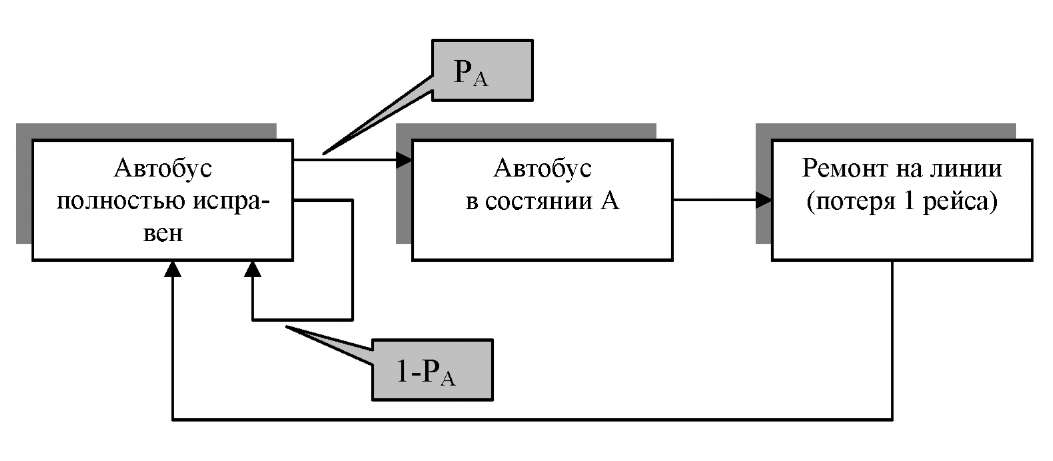
Рис. 2.2 Правило ремонта

(или эксплуатационная политика)

Для изучения схемы на рис. 2.2 необходимо описать смысл всех введенных связей между блоками. Обратите внимание, что блок «Ремонт на линии»

вообще говоря не является состоянием, поскольку неизвестна вероят­ность перехода из предыдущего состояния.

Очевидно, что эксплуатационная политика в будет изображаться более сложным графом (рис. 2.3).

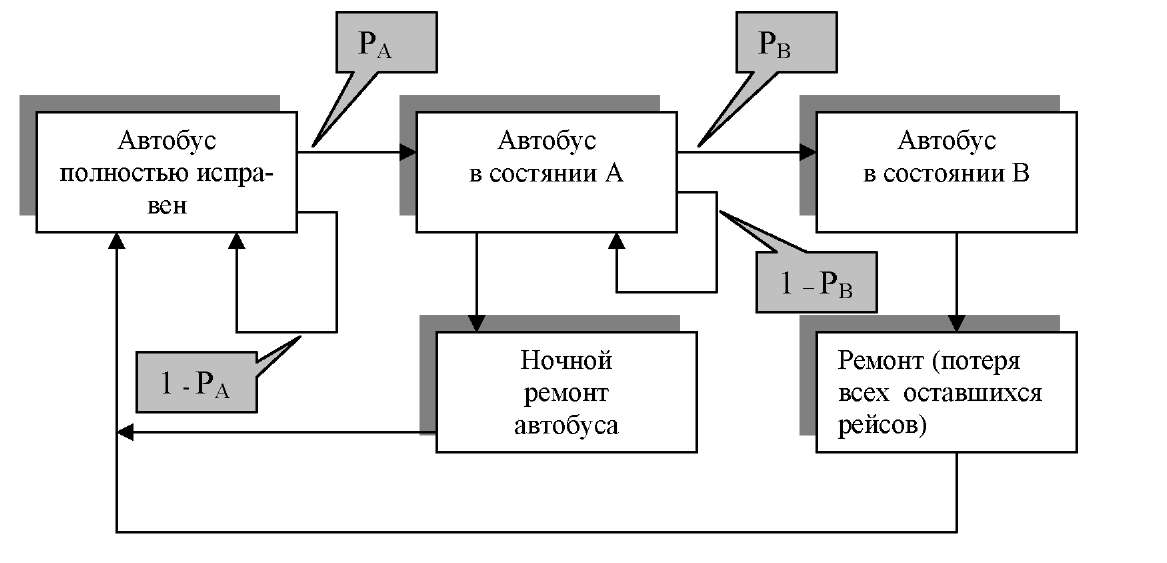
Рис. 2.3 Эксплуатационная политика

Теперь становится ясным, что графы переходов отражают последова­тельность некоторых событий, наступающих с заданными вероятностями и эту последовательность событий можно представить в виде имитаци­онной модели в схеме случайных дискретных событий.

В табл.1 сведены все возможные состояния и соответствующие вероят­ности переходов.

Таблица 1. Выборка состояний автобуса в конце рейса

Автобус выезжает в рейс в состоянии	Автобус приезжает в парк в состоянии
	Исправное	А	В
Исправное А	a < R < 1	0 < R < a b < R < 1	0 < R < b

При моделировании мы производим выборку случайного числа R и с по­мощью данных табл. 1 имитируем состояние, в котором находится авто­бус.

Пусть, например, автобус начинает рейс в состоянии А (это возможно только при стратегии ). Если полученное значение R удовлетворяет не­равенству , то автобус и заканчивает рейс в состоянии А. При этом:

Это выражение показывает, что принятая выборочная процедура имеет нужные для данной модели вероятности перехода.

Мы описали задачу обслуживания автобуса, но очевидно, что ее можно применить к обслуживанию любых других машин.

Блок-схема имитационной модели

Заметим вначале, что можно проводить моделирование дней для стратегии а и затем дней для стратегии . Т.е. составить две про­граммы для двух стратегий. На рис. 2.4, однако, представлен более эко­номичный алгоритм, в котором вначале совершается (имитируется) один рейс при стратегии а и затем при стратегии Р; затем совершается сле­дующий рейс, опять вначале при стратегии а, затем при стратегии р и т.д. При этом мы более эффективно используем генератор базовых случайных чисел.

На блок схеме оставлены авторские обозначения переменных (Клейнен Дж. «Статистические методы в имитационном моделировании», кн. 1).

SG1 - логическая переменная «хорошее состояние при - стратегии»; принимает значение 1, если автобус находится в хорошем состоянии при -стратегии; и значение 0, если автобус находится в состоянии А (также при -стратегии);

SG2 - логическая переменная «хорошее состояние при - стратегии»; равна 1, если автобус находится в хорошем со­стоянии при 2-й стратегии, и 0, если автобус в состоянии А;

SB2 - логическая переменная «состояние В при -стратегии»; равна 1, если автобус находится в состоянии В при 2-й стратегии, и 0 в иных случаях;

DMAX - число дней, которые мы хотим моделировать;

D - текущее число дней при моделировании;

RM - число моделируемых рейсов в день, включая отдельные рейсы;

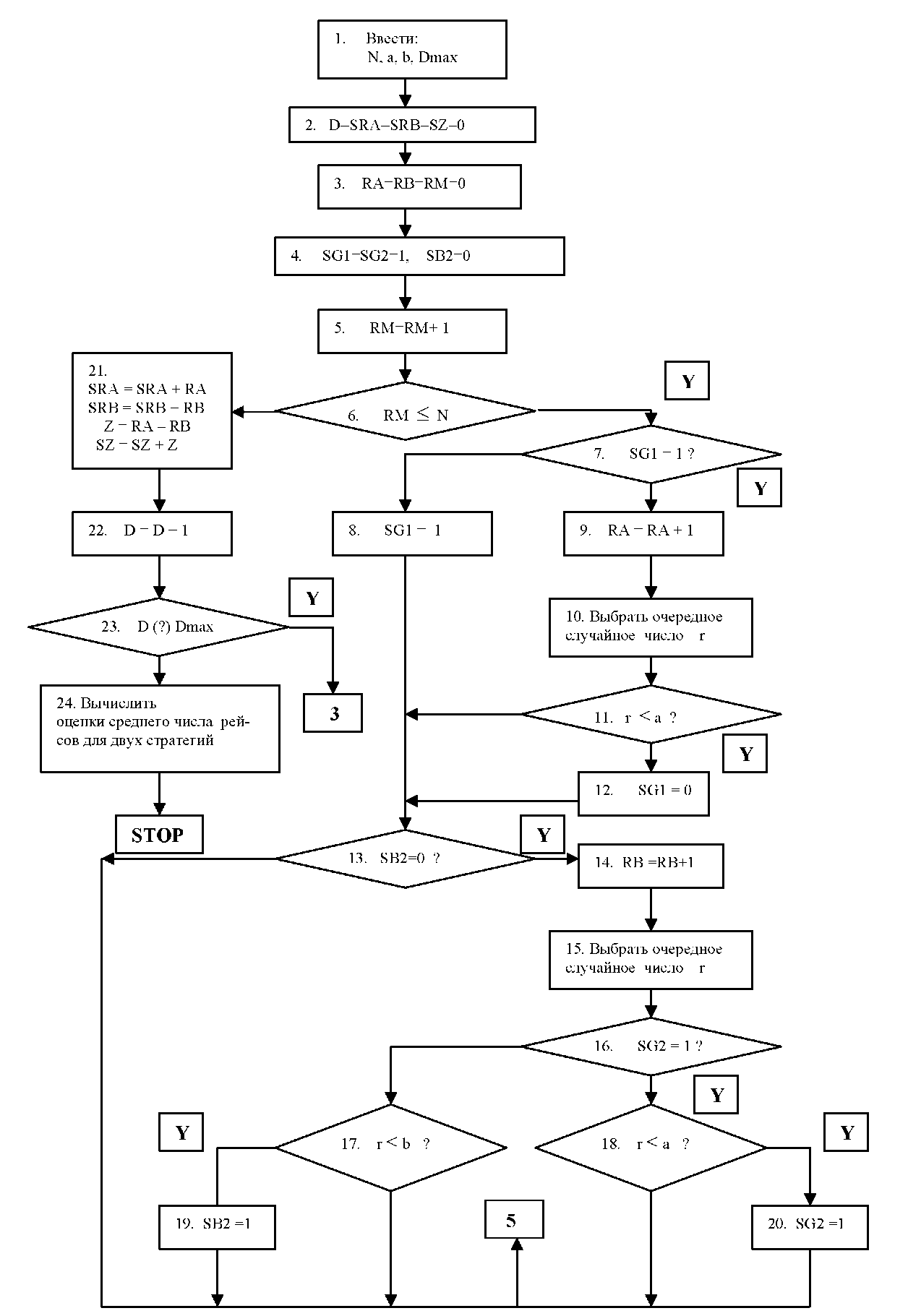
Рис. 4 Алгоритм имитации и -стратегий обслуживания автобусов

RA, RB - число действительно выполненных рейсов в течение дня при стратегиях и соответственно;

SRA, SRB - общее число рейсов в течение D дней при стратегиях и соответственно;

Z = (RA - RB) -разность между числом действительно выполнен­ных рейсов при разных стратегиях;

SZ - сумма значений Z за D дней;

Заметим, что для учебных целей блоки 23, 24 описаны не формально — конкретные операции требуют самостоятельного программирования.

Естественно, что при составлении собственной программы имитации, можно выбирать не только другие переменные, но и другую структуру программы.

Аналитическая модель для выбора варианта обслуживания.

В настоящее время известно аналитическое решение рассматриваемой задачи, т.е. формулы, определяющие среднее количество рейсов и . Для удобства записи формул обозначим:

- вероятность перехода в состояние А ;

- вероятность перехода в состояние B.

Тогда среднее количество рейсов для двух стратегий определяется сле­дующими соотношениями:

где N - планируемое число рейсов в день.

Таким образом, зная вероятности , и N по приведенным формулам можно всегда вычислить среднее число рейсов для разных стратегий обслуживания, и выбрать такую стратегию, которая обеспечит макси­мальное ожидаемое количество рейсов при данных конкретных пара­метрах модели.

Однако для практически важных задач, которые имеют гораздо более сложную структуру, аналитическое решение либо невозможно, либо на­столько сложно, что является недоступным для инженера. Кроме того, аналитический метод не обладает той гибкостью, которая присуща ме­тоду имитационного моделирования. Термин «гибкость» здесь означает, что параметры имитационной модели, как правило, можно достаточно просто и быстро изменить в соответствие с изменением исходных дан­ных и получить новое решение.