9Лабораторная работа №9. Исследование - канальной смо с ожиданием

Цель работы: изучить систему массового обслуживания с ожиданием и ее харак­теристики.

Краткие теоретические сведения

СМО с - каналами обслуживает простейший поток требований. При занятости всех n узлов обслуживания поступившее требование ставится в очередь и обслуживается после некоторого ожидания. Общее число требований, находящихся в системе на обслу­живании и в очереди, обозначим и назовем состоянием системы. При величина к характеризует число занятых каналов в системе, при , да число занятых каналов равно , а разность определяет длину очереди. Параметр интенсивности обслуживания потока определяется числом занятых узлов, и в первом случае зависит от состояния системы , а во втором имеет постоянное значение .

Введем понятие загрузки системы равное отношению интенсивности входящего потока к интенсивности обслуживания:

Отметим, что при интенсивности поступающей нагрузки , равной или больше числа узлов обслуживания системы , с вероятностью равной 1 постоянно будут заняты все узлы обслуживания и длина очереди будет бесконечной - явление «взрыва». Поэто­му, чтобы система могла функционировать нормально и очередь не росла безгранично, необходимо выполнить условие .

Вероятность того, что система в установившемся режиме находится в состоянии определяем по формуле (второе распределение Эрланга)

(1)

где .

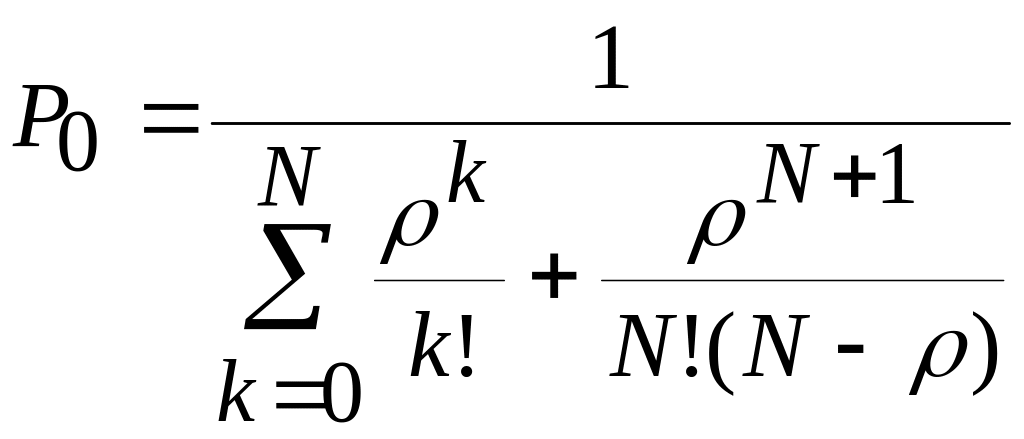К основным характеристикам качества обслуживания СМО с ожиданием относят следующие.

Вероятность наличия очереди есть вероятность того, что число требований в системе больше числа узлов:

Вероятность занятости всех узлов системы :

Среднее число требований в системе :

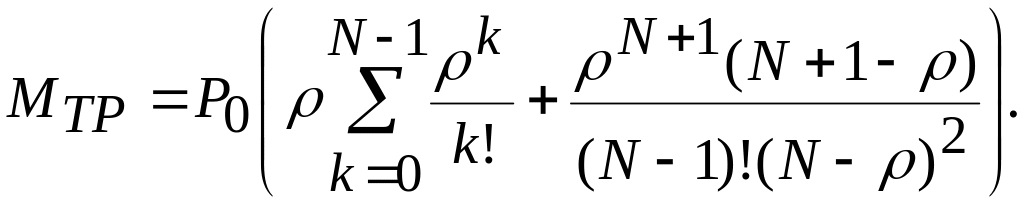
Средняя длина очереди :

Среднее число свободных узлов :

Среднее число занятых узлов :

Среднее время ожидания начала обслуживания для требования, поступившего в систему:

Общее время, которое проводят в очереди все требования, поступившие в систему за единицу времени :

Среднее время , которое требование проводит в системе обслуживания:

Суммарное время, которое в среднем проводят в системе все требования, посту­пившие за единицу времени :

1 Лабораторная работа №1 6

МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ ЧИСЕЛ ЗАДАННЫМ ЗАКОНОМ РАСПРЕДЕЛЕНИЯ 6

Варианты лабораторных работ 18

2 Лабораторная работа №2 20

АНАЛИЗ ВАРИАНТОВ ОБСЛУЖИВАНИЯ АВТОБУСОВ НА ОСНОВЕ ИМИТАЦИОННОЙ МОДЕЛИ 20

3 Лабораторная работа №3 28

ИССЛЕДОВАНИЕ И ОПТИМИЗАЦИЯ СИСТЕМЫ КОНТРОЛЯ 28

4 Лабораторная работа №4 37

МОДЕЛИРОВАНИЕ СИСТЕМ 37

5 Лабораторная работа №5. 44

6 Лабораторная работа №6. 52

7 Лабораторная работа №7. 57

8 Лабораторная работа №8. 60

Моделирование реального процесса обслуживания СМО с отказами 60

9 Лабораторная работа №9. 62

Исследование - канальной СМО с ожиданием 62

10 Лабораторная работа №10. 67

Моделирование реального процесса обслуживания СМО с неограниченной очередью 67

73

Число кана­лов обслуживания определяется из таблицы 1.

Таблица 1

	1,5,9,13,17,21	2,6,10,14,18,22	3,7,11,15,19,23	4,8,12,16,20,24
	3	4	5	6

Для СМО с ожиданием график распределения , построенный в системе MathCad, показан на рис. 8.1.

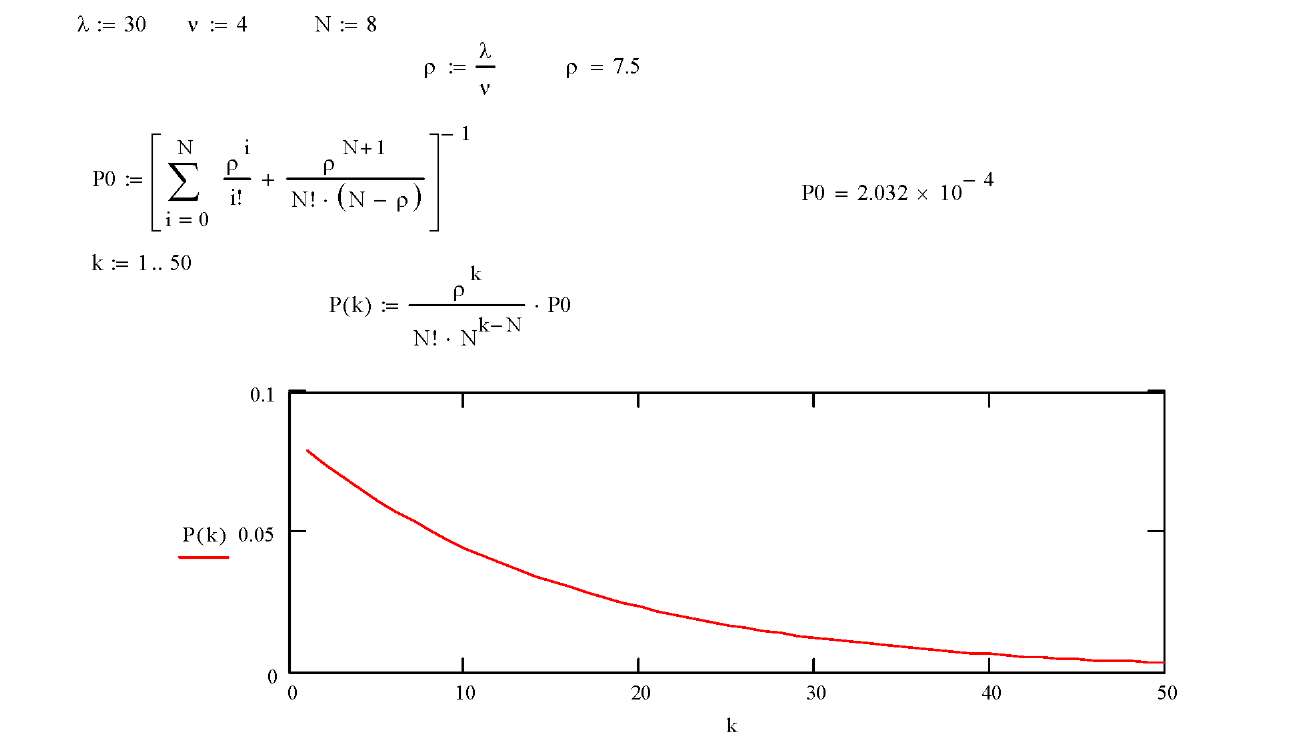
Рис. 8.1. График вероятностей

Определить характеристики качества обслуживания:

1. Вероятность наличия очереди .

2. Вероятность занятости всех узлов системы .

3. Среднее число требований в системе .

4. Среднюю длину очереди .

5. Среднее число свободных узлов .

6. Среднее число занятых узлов .

7. Среднее время ожидания .

8. Общее время пребывания требований в очереди за единицу времени .

9. Среднее время пребывания требований в системе .

10. Суммарное время, которое проводят все требования в системе за единицу вре­мени, .