4.1. Общие сведения

Тепловой режим горных выработок зависит от таких факторов, как температура поступающего в выработку воздуха, температура пород, влажность рудничной атмосферы, скорость движения и ко­личество проходящего по выработкам воздуха и др. Изучение теп­лового режима и управление им имеют большое значение для соз­дания санитарно-гигиенических условий.

Кроме того, при нарушении нормального теплового процесса может быть нарушена нормальная работа шахтного подъема и вен­тиляторной установки вследствие обмерзания устьев стволов, ра­бочих лопаток п каналов вентиляторов в зимнее время. Устойчи­вость выработок, проведенных по породам многолетней мерзлоты,

42

может быть нарушена в теплое время года вследствие проникно­вения в выработки теплого воздуха и оттаивания мерзлого грунта.

Большое влияние тепловые условия оказывают на самочувствие трудящихся. Влияние тепла на человека объясняется тем, что в человеческом организме в процессе жизнедеятельности в зависимо­сти от выполняемой нагрузки образуется тепла 168—1680 кДж/ч. Для поддержания постоянной температуры человеческого тела все образовавшееся тепло должно быть выведено из организма.

Выделение тепла организмом происходит за счет лучеиспуска­ния, конвекции и испарения пота. Теплоотдача за счет лучеиспус­кания зависит от разности температур человеческого тела и окру­жающей среды и в тех случаях, когда температура воздуха, окру­жающих поверхностей и одежды близка к 30 °С, практически при­ближается к нулю. Теплоотдача за счет конвекции обусловлена удалением с поверхности тела нагретых слоев воздуха и зависит от скорости движения вентиляционной струи. Теплоотдача, вызванная испарением влаги с поверхности тела, объясняется тем, что на ис­парение 1 г влаги затрачивается около 2,5 кДж тепла. Интенсив­ность теплоотдачи в этом случае зависит от скорости испарения влаги, которая возрастает с уменьшением относительной влажности воздуха.

Температура воздуха в горных выработках зависит от глубины разработки; тепловых процессов, происходящих в горных выработ­ках; температуры поступающего в горные выработки воздуха; сжа­тия воздуха с глубиной и, как следствие, увеличения температуры; интенсивности проветривания.

С увеличением глубины расположения горных выработок уве­личивается температура горных пород, что приводит к увеличению температуры воздуха вследствие теплообмена.

Ожидаемая средняя температура горных пород (в °С) с уве­личением глубины расположения выработки Н может быть опре­делена по формуле

t_n._cp = tn, + (H-H₀)/r_cT, (4.1)

где t„.₃ — температура пород нейтральной зоны (зоны с постоян­ной температурой горных пород) в данной местности, °С; Н₀ — глубина нейтральной зоны от поверхности, м; Г_ст — геотермиче­ская ступень, м/°С. Значения Н₀, t_u.₃, Г_ст принимаются по табл. 8.

В целях создания нормальных температурных условий в гор­ных выработках шахт Правилами безопасности регламентируются температура и скорость движения воздуха на рабочих местах. Мак­симальная температура воздуха в горных выработках не должна превышать +26°С.

Минимальные скорости движения воздуха в призабойных про­странствах у забоев подготовительных выработок установлены равными 0,15 м/с при температуре воздуха /= + 15°С; 0,3 м/с при /=15-^20°С; 1,0 м/с при ^ = 20-^22 °С; 1,5 м/с при / = 22ч-24°С и 2 м/с при t = 24ч-26 °С. При температуре воздуха менее +15°С

43

скорость движения его в выработке в негазовых шахтах не долж­на превышать 0,3 м/с.

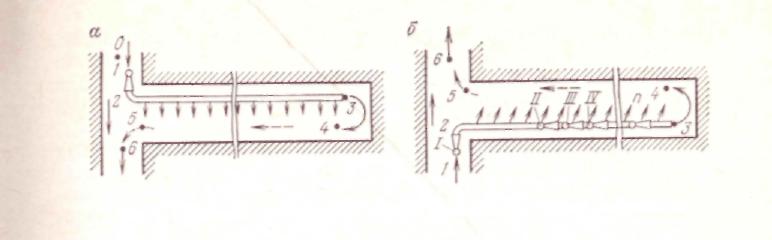
Рис. 17. Схемы вентиляции забоев тупиковых горных выработок

При нагнетательном способе вентиляции тупиковых выработок (рис. 17, а) ожидаемая температура воздуха (°С) в характерных пунктах (/—6) определяется по следующим зависимостям:

t₃ = {[4(1 ~М)±М_СЖ]Л + 2ЫЩ/[Л + N(M + 2M -2)]; (4.4) к = [П— Ъ{М — \)]1Л\ (4.5)

t_b = J£f₄ + (1 — 2N — 0,5£ + 2,45жр₄) t, + N (t₂ + t₃) —

Параметры рудничного воздуха в магистральной выработке, проветриваемой сквозной струей за устьем тупиковой выработки (пункт 6 на рис. 17,а), определяются по / — d диаграмме для соответствующего давления как параметры смеси двух известных объемов воздуха.

При нагнетательном способе проветривания тупиковых горных выработок значительной длины с помощью последовательно уста­новленных вентиляторов (I; II, ..., п) ожидаемая температура воз­духа в соответствующих пунктах (рис. 17,6) определяется по фор­мулам:

где Л/цмп — приращение температуры от работы вентилятора мест­ного

проветривания, °С.

Тепловыделение в тупиковых горных выработках. При расчете тепловыделения в тупиковой горной выработке значения удельной теплоемкости С_м, коэффициентов теплопроводности К и темпера­туропроводности а горного массива принимаются средневзвешен­ными по периметру и длине выработки.

Тепловыделение (кДж/ч) при охлаждении горных пород можно определить по формуле

4.3. Меры борьбы с высокими температурами в горных выработках

Нормальные тепловые условия в горных выработках обеспечи­ваются при предупреждении нагревания шахтного воздуха, конт­роле за необходимым расходом и скоростью его движения на уча­стке по тепловому фактору, теплоизоляции и тщательной гермети­зации воздухоподающих трубопроводов, предупреждении окисли­тельных процессов, тепло- и гидроизоляции стенок выработок.

В случаях, когда предупредить нагревание воздуха невозможно, применяется искусственное его охлаждение в системах кондицио­нирования. Различают следующие основные типы холодильных установок: с охлаждением воздуха на поверхности; с охлаждением воздуха на горизонте при размещении холодильных машин на по­верхности; с размещением всего холодильного оборудования на го­ризонте; передвижные холодильные установки.

Для поверхностных установок необходимо более глубокое ох­лаждение воздуха, так как по пути движения его по горным выра­боткам происходят нагревание и повышение температуры. Под­земные холодильные установки должны обладать компактностью,

49

удобством обслуживания, надежностью в работе, безвредностью, взрыво- и пожаробезопасностыо.

В качестве рабочих жидкостей в холодильных машинах исполь­зуют в основном фреоны — фреон-12 (дифтордихлорметан CF₂C1₂), фреон-22 (CHF₂C1).

Для охлаждения воздуха в тупиковых горных выработках при­меняются следующие передвижные кондиционеры: КПШ-3 произ­водительностью 350 МДж/ч; КПШ-40 производительностью 165 МДж/ч и КПШ-40П производительностью 160 МДж/ч.

При разработке крутых угольных пластов, опасных по внезап­ным выбросам, в целях безопасности используется пневматическая энергия. В таких случаях целесообразно применять воздушные хо­лодильные машины, в которых сжатый воздух с температурой около +30°С поступает непосредственно от шахтной сети в турбо-детандер. При расширении сжатый воздух охлаждается до —45 °С и, смешиваясь с вентиляционной струей, поступает в забой.

4.4. Подогрев подаваемого в шахту воздуха

Поскольку в большинстве районов СССР в зимнее время тем­пература атмосферного воздуха отрицательна, возникает опасность обмерзания воздухоподающих выработок с образованием наледей, нарушения нормальной работы шахтного подъема, обледенения лестничных отделений, нарушения несущей способности крепи и т. п. Поэтому зимой подаваемый в шахту воздух должен подогре­ваться с тем, чтобы температура его была не ниже +2°С.

Подогрев воздуха осуществляется обычно паровыми калори­ферами и в отдельных случаях — электрокалориферами. Как пра­вило, подогревается сравнительно небольшая часть общешахтного воздуха (20—25%) до температуры 60—70 °С с тем, чтобы после смешивания с основной вентиляционной струей температура смеси равнялась +2°С.

Подогретый воздух подается вентилятором по специальному каналу в ствол, где происходит смешивание его с основной вен­тиляционной струей, поступающей через устье ствола. Такая схема неудобна тем, что устье ствола должно быть открытым, в резуль­тате чего в зимнее время создаются неблагоприятные условия для работы людей и механизмов на приемной площадке.

Возможна схема подогрева, при которой над устьем воздухо-подающего ствола сооружено утепленное надшахтное здание. При этой схеме свежий воздух поступает в специальную будку, из ко­торой проходит в канал, где смешивается с подогретым воздухом. Смешанный воздух поступает в ствол через специальные окна в стенах ствола, расположенные ниже нулевой отметки.

Для выбора калорифера необходимо определить теплопроиз­водительность калориферной установки, а также количество по­догреваемого воздуха и температуру подогрева.

Введем обозначения: бобщ — массовый дебит поступающей в шахту воздушной струи, кг/мин; (}_Под — массовый дебит подогреваемой части воздуха,

ЧАСТЬ ВТОРАЯ

ВЕНТИЛЯЦИЯ ГОРНЫХ ВЫРАБОТОК, ТОННЕЛЕЙ И КАМЕР ПРИ ИХ СООРУЖЕНИИ

5. АЭРОГАЗОДИНАМИКА ГОРНЫХ ВЫРАБОТОК

5.1. Виды давления в движущемся воздухе. Депрессия

Виды давления. Любое движение воздуха происходит в преде­лах земной атмосферы, причем так, что над областью движения всегда находятся слои воздуха, оказывающие давление на каждый объем движущегося воздуха. Таким образом, аэродинамиче­ское давление —давление вышележащих слоев воздуха — является первой составной частью полного давления движущегося воздуха.

Из механики известно, что любое движущееся материальное тело обладает кинетической энергией и что в случае встречи тела с какой-либо преградой оно окажет на преграду давление, которое будет зависеть от кинетической энергии тела. Являясь материаль­ной субстанцией, движущийся воздух полностью подчиняется от­меченным законам.

Если в поток воздуха поместить какое-либо тело, например пла­стину, то движущийся воздух будет оказывать на нее давление, определяемое его кинетической энергией. Это давление называет­ся динамическим и"ли скоростным. Таким образом, дина­мическое (скоростное) давление является составной частью пол­ного давления движущегося воздуха.

Энергетическая интерпретация давления. Рассмотрим сущест­вующие в движущемся воздухе давления с энергетической точки зрения. Выделим в неподвижной атмосфере некоторый объем воз­духа, находящийся под аэростатическим * давлением р. Если во­круг него создать разрежение, то рассматриваемый объем начнет расширяться до тех пор, пока давление внутри него не будет равно давлению снаружи. При этом расширяющимся объемом воздуха будет совершена работа. Следовательно, уменьшение статического давления воздуха сопровождается выполнением определенной ра­боты. Данное обстоятельство свидетельствует о том, что статиче­ское давление является одной из форм энергии, а именно потен­циальной энергией, которая при определенных условиях мо­жет переходить в работу. Поэтому статическое давление воздуха

* В дальнейшем в целях сокращения аэростатическое давление будем на­зывать статическим.

52

можно определить как потенциальную энергию, характеризующую работу, которую может совершить данный объем воздуха при его расширении до конечного давления р = 0.

Поскольку причиной динамического давления является движе­ние воздуха, очевидно, что оно характеризует кинетическую энергию воздуха. Кинетическая энергия тела массой М, движу­щегося со скоростью и,

Е_н = Ми²/2, (51)

а отнесенная к единице его объема

е_к = yu²/2g,

где у— удельный вес тела; g — ускорение свободного падения.

Если принять, что вся кинетическая энергия переходит в дина­мическое давление, т. е. что p_ium = e_H, то

Рдин = 7"²/2£. (5.2)

Поскольку скорость и в общем переменна в пространстве, ди­намическое давление является функцией точки. В частности, оно изменяется в поперечном сечении выработки, в то время как статическое давление во всех точках поперечного сечения практи­чески одинаково.

Полная энергия единицы объема воздушного потока равна сум­ме его потенциальной и кинетической энергий. Поскольку потен­циальная энергия потока характеризуется его статическим давле­нием рст, а кинетическая — динамическим р_дш„ то полное давление

Рп = Рст + Рд.ш- С⁵-³)

Измерение статического и динамического давления в потоке. Для движущегося воздуха справедлив закон Паскаля, согласно которому статическое давление действует на все плоскости в пото­ке,- включая боковые стенки воздухопроводов и поверхности тел, находящихся в потоке (рис. 18). В то же время динамическое дав­ление воздушного потока действует на поверхности, расположен­ные поперек движения воздуха. Вследствие этого, например, дина­мическое давление будет действовать лишь на поверхность пла­стины (см. рис. 18), обращенную навстречу потоку. Оно не дейст­вует на плоскости, параллельные потоку, например на стенки

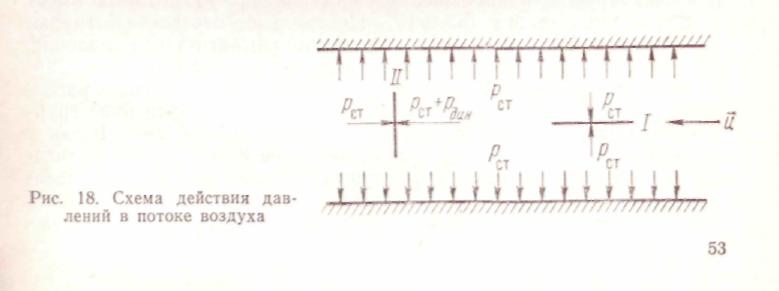
воздухопровода, если последние параллельны направлению движе­ния воздуха. Из сказанного, в частности, следует, что пластина / на рис. 18 будет находиться в равновесии, а пластина // — под действием силы р_лш^=[(Рст+Ртн) — Рст]5 (5 — площадь пласти­ны), направление которой совпадает с направлением скорости и.

Особенности действия давлений р_СТ и р_тп в потоке обусловили специфику их замера. Для замера статического и скоростного дав­лений применяются приемники различной конфигурации, чаще-всего в виде полых трубок, внутреннее пространство которых со­общается с потоком через специальные отверстия. Приемник ори-

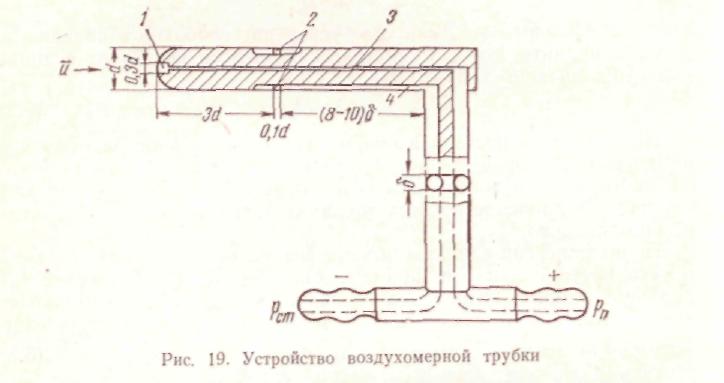
ентируется в потоке так, что выходные плоскости этих отверстий располагаются либо параллельно направлению движения воздуха, либо перпендикулярно к нему. Тогда плоскости отверстий, перпен­дикулярные к потоку, будут воспринимать полное давление в точке их расположения р_и, а" плоскости отверстий, параллельные пото­ку _f _ _ег0 статическое давление р_Ст- Отводя эти давления от при­емников на измерительный прибор, можно замерить отдельно р„,

р_СТ и их разность р_п — рст^Рдош-

Описанный принцип измерения используется в ряде пневмомет-рических трубок, наибольшее распространение из которых имеет воздухомерная трубка (рис. 19). Центральное отверстие / трубки расположено навстречу потоку, оно воспринимает полное давление. Щелевое отверстие 2, расположенное на боковой поверхности нако­нечника, воспринимает статическое давление. Действующие на от­верстия 1 и 2 давления р_а и р_ст передаются через внутренние труб­ки 3 и 4 на выходные штуцеры со знаками « + » и «—». Щель 2 должна находиться на расстоянии не менее 3d от носка наконеч­ника, чтобы создаваемое им возмущение давления исчезло и аосо-лютное давление на боковой поверхности наконечника стало рав­ным или достаточно близким р_с7. В то же время эта щель не долж-

54

на находиться близко от ножки трубки, чтобы не воспринимать создаваемых ею возмущений давления.

Депрессия. Депрессией в рудничной вентиляции называется раз­ность давлений. Разность статических давлений называется ста­тической депрессией, разность скоростных давлений — с ко­рост и ой депрессией (или разностью скоростных давлений), разность полных давлений — полной депрессией.

5.2. Основные законы движения воздуха в горных выработках

Движение воздуха в шахтах подчиняется тем же основным за­конам, что и остальные физические явления материального мира, а именно: закону сохранения массы и закону сохранения энергии. Эти фундаментальные законы применительно к движению воздуха в горных выработках определяют основные характеристики шахт­ных вентиляционных потоков. К этому следует добавить второй закон Ньютона, или закон количества движения, позволяющий по­дучить уравнение движения воздуха, связывающее основные харак­теризующие движение величины.

Закон сохранения массы применительно к движению воздуха можно сформулировать следующим образом: масса любого объема воздуха остается постоянной в процессе его движения. Иными словами, изменение массы во времени

равно нулю.

Если в потоке воздуха выделить элементарный объем со, доста­точно малый, чтобы плотность воздуха в нем р можно было счи­тать постоянной, то закон сохранения массы можно записать так:.

d(p(o)/dt = 0, (5.4)

где рсо — масса выделенного объема; / — время.

Уравнение (5.4) можно записать через проекции скорости по­тока и, v и w в рассматриваемой точке на оси координат:

dp/dt + д (ри)/дх + д (pv)/dy + д (pw)/dz = 0. (5.5)

Уравнение (5.5) называется уравнением неразрывно­сти. Между полной производной во времени в (5.4) и частной про­изводной во времени в (5.5) существует различие; полная произ­водная учитывает изменение дифференцируемой величины как вследствие развития процесса во времени, так и вследствие пере­мещения рассматриваемого объема в пространстве, в то время как частная производная во времени не учитывает перемещения в про­странстве.

Для стационарного давления, при котором характеристики по­тока (плотность, скорость, давление и др.) в некоторой фиксиро­ванной точке пространства не изменяются во времени, dp/dt = 0 и уравнение неразрывности будет иметь вид

д (ри)/дх + д (pv)/dy + д (pw)/dz = 0, (5.б)

55

а при р = const

ди/дх + dv/ду = dw/dz = 0. (5.7)

В выработке постоянного сечения v = w = 0 имеем

и = const,

т. е. скорости воздуха в сходственных точках постоянны.

Из уравнения (5.7) следует, что в однородном по плотности по­токе увеличение скорости в одном направлении должно вызывать соответствующее уменьшение ее в другом.

Из уравнения неразрывности (5.4) для изотермического потока следует уравнение расхода:

u₁S₁ = u₂S₂, (5.8)

где Si и S₂ — площади начального и конечного сечений элементар­ной струйки потока*; щ и и₂— скорости движения воздуха через эти сечения.

Интегрируя правую и левую части уравнения (5.8) по всему сечению выработки, получим

Q₁ = Q„ (5.9)

т. е. объемный расход воздуха в выработке является величиной постоянной. Уравнение (5.9) не соблюдается при разветвлении струй и утечках воздуха из выработки, а для неизотермических потоков вместо него следует записать

М, = М₂,

где М\ и М₂ — массовые расходы воздуха соответственно в началь­ном и конечном сечениях.

Закон сохранения энергии. Для случая движения воздуха закон сохранения энергии может быть сформулирован следующим обра­зом :изменение энергии произвольного объема воздуха за некоторый промежуток времени при его движении равно сумме количества сообщен­ного ему тепла и работы приложенных к объему внешних сил за то же время, т. е.

Д£_вн + Л£_п + Д£„ = /AQ + АЛ, (5.10)

где А£_Вн — изменение внутренней энергии данного объема воздуха, определяемой кинетической энергией движения молекул и потен­циальной энергией их взаимодействия; Д£_п — изменение потен­циальной энергии этого объема, определяемое его перемещением

* Под элементарной струйкой понимается участок потока малого поперечного сечения, ограниченный с боков линиями тока, проходящими через контур сече­ния. Под линией тока понимается линия, касательная к векторам скорости час­тиц, расположенных на ней. Сечение струйки выбирается настолько малым, чтобы скорости воздуха во всех его точках можно было принимать постоянными.

56

по вертикали; Д£_1ч-— изменение кинетической энергии объема; / — механический эквивалент тепла; AQ — количество тепла, полученное (отданное) дан­ным объемом воздуха; АЛ — работа внешних сил.

Внешними силами при дви­жении воздуха по выработке являются силы трения о ее стенки и силы статического давления, приложенные к по­верхности рассматриваемого объема.

В случае адиабатического движения несжимаемой жидкости, которой можно считать воздух при существующих в шахте давлениях, AE_BU = AQ=0. При этом условии для установившегося движения элементарной струйки воздуха соотношение (5.10) может быть записано в виде

(5.ii;

— dp + dz + duV2g + dh = 0,

Y

где p — давление воздуха; z — аппликата центра тяжести сечения струйки относительно произвольной горизонтальной плоскости сравнения; и — скорость воздуха в рассматриваемом сечении струнки; h — работа внешних сил, отнесенная к единице массы воздуха.

Уравнение (5.11) называется уравнением Вернул л и в дифференциальной форме (по имени русского ученого Даниила Берпулли, впервые получившего это соотношение в 1738 г.).

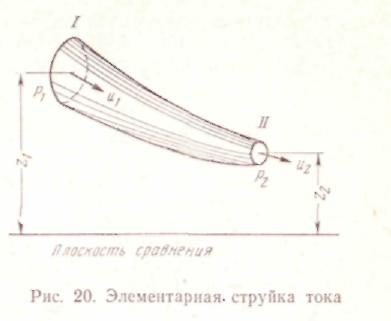
Интегрируя выражение (5.11) вдоль струйки от сечения / до сечения 77 (рис. 20) при y = const, получим

(5.12)

(Pi — Рз) + 7 & — z,) + 7 ("? — ul)/2g = h.

Уравнение (5.12) может быть записано для случая равного удельного веса воздуха в / и // сечениях и для всего потока в вы­работке в виде

(Pi — Ра) + (Yi*i — Уй) + (fciYi"?/2g — Ь.^А/Ц) = К (5-13)

где р\—Р2 — разность статических давлений воздуха в сечениях / и //; Yi²i —У2^г2 — разность давлений двух столбов воздуха, име­ющих высоту Z\ и z₂ и удельный вес у_х и у₂; k_xy_xu²\l2g—k₂y₂u²₂/2g— разность динамических давлений в сечениях I и //; щ и и₂ — сред­няя скорость движения воздуха в сечениях I и II.

Коэффициенты /г, и k₂ в уравнении (5.12) называются коэф­фициентами кинетической энергии и учитывают не-

равномерность распределения скоростей движения воздуха в сече­ниях / и // выработки. Их можно определять по формулам: для круглых штрекообразных выработок

k= 1 +213«;

для штрекообразных выработок, закрепленных неполными ра­мами,

k = 0,810 + 282а,

где а — коэффициент трения.

Величина h в уравнении (5.13) обозначает работу всех внешних сил при перемещении рассматриваемого объема воздуха из сече­ния / в сечение //. Роль внешних сил может заключаться в умень­шении первоначальной энергии воздуха (силы сопротивления) или в ее увеличении (например, при работе вентиляторов); в первом случае /i>0, во втором /г<0.

В уравнении (5.13) первые два слагаемых в скобках представ­ляют собой изменение потенциальной энергии потока, третье — изменение его кинетической энергии. Как видно, изменение полной энергии потока между двумя произвольными его сечениями равно энергии, затраченной на преодоление сопротивлений движению воздуха на этом участке (/i>0), или поступлению энергии в поток (КО), или тому и другому одновременно.

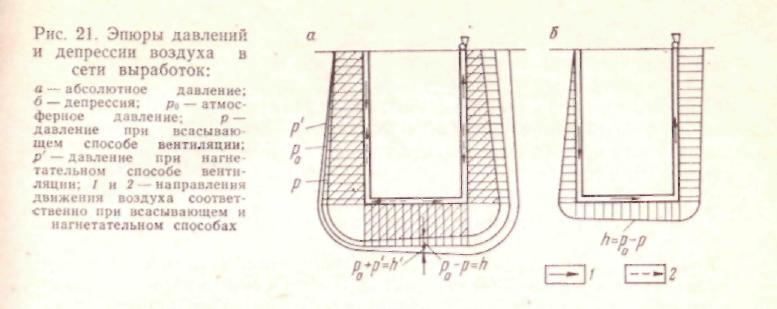
Следует иметь в виду, что р₂ в уравнении (5.13) не является атмосферным давлением на глубине z₂. Действительно, полагая для простоты Yi⁼Y2 ⁼ Y> уравнение (5.13) можно переписать:

(Pi — Р₂) + (Ш — У&) + UiYi"i/2g — k₂y₂u\l2g) = = р! + yAz — р₂ + Др_дин = р₀₂ — р₂ + Дрд_ИН = h_u (5.14)

где

Дг = z_l —2₂;

АРдин = £iYi«?/2g — k₂y₂u₂/2g;

p₀₂ = pi-\-yAz — атмосферное давление на глубине z₂. Из уравнения (5.14) следует, что

Pi = A» —{k — ДРдаш),

т. е. что р₂ — атмосферное давление на глубине z₂, уменьшенное на величину потерь энергии и на разность динамических давлений между сечениями / и //.

На рис. 21 представлены эпюры давлений и депрессий в шахте при Др_д,ш = 0.

Важным следствием из уравнения Бернулли является тот факт, что при h = const изменение и в сечении вызывает обратное изме­нение р. Действительно, при увеличении и₂ давление р₂ должно уменьшаться, чтобы было соблюдено условие h = const. Справед­ливо и обратное заключение. Следовательно, увеличение скорости

движения воздуха в сечении (например, вследствие его уменьше­ния) вызывает уменьшение в нем статического давления, и наобо­рот.

Уравнение Бернулли является одним из основных уравнений рудничной аэродинамики, ибо, являясь математической формули­ровкой закона сохранения энергии, оно объединяет все основные величины, необходимые для решения любой аэродинамической задачи.

В уравнении (5.13) все члены имеют размерность давления. Иными словами, уравнение Бернулли выражает баланс потенци­альной и кинетической энергии единицы объема потока.

Разность давлений (р_х—р₂) является следствием работы вен­тилятора и называется депрессией вентилятора h_B. До­полнительная разность давлений (yiZi — y₂z₂) создается естествен­ными факторами и называется депрессией естествен­ной тяги h_e. Обозначив Др_дип через k_miu уравнение (5.13) при­ведем к виду

(5.15)

K±h_e± Л_дин - к.

Здесь h_B±h_mH представляет собой изменение получаемой от вен­тилятора полной энергии потока между сечениями / и //, т. е.

h_mn±h = h. (5.16)

Депрессия естественной тяги может увеличивать энергию потока (/г_е>0) или играть роль сопротивления (h_e<0). Аналогичное влия­ние на поток могут оказывать и другие факторы (открытые пото­ки пульпы в выработках гидрошахт, ветер, дующий в устье выра­ботки, и др.). Обобщая уравнение Бернулли на случай нескольких источников энергии и на все возможные виды сопротивлений дви­жению, можно написать

Kn = h_v (5.17)

где h_Bn — энергия единицы объема воздуха, поступающая от внеш­них источников.

Из уравнения (5.17) вытекает следующая общая формулировка закона сохранения энергии при движении воздуха по выработкам: при установившемся движении воздуха по вы­работкам энергия, поступающая в поток от внешних источников, полностью расходуется на преодоление всех сопротивлений на пути движе­ния воздуха.

5.3. Режимы движения воздуха в шахтах

Движение воздуха по любому каналу может быть спокойным, характеризующимся обычно малыми скоростями, параллельными траекториями частиц и отсутствием перемешивания между отдель­ными слоями потока,— ламинарным либо бурным, характери­зующимся беспорядочным перемещением отдельных частиц и хао­тическим перемешиванием между слоями потока, — турбулент­ным.

Если средняя скорость потока постоянна, то скорость и давле­ние потока в точке при ламинарном движении не изменяются во времени, т. е. движение является стационарным. При турбу­лентном движении даже в случае постоянства его средней скорости точечные характеристики потока изменяются во времени, пульси­руют, вследствие чего лишь осредиенные по времени их значения оказываются постоянными, а движение является квазистацио­нарным.

Пульсации турбулентного движения являются проявлением существующих в нем вихрей самых различных размеров,

Основное различие между ламинарным и турбулентным режи­мами движения состоит в механизме переноса субстанции: в лами­нарном этот перенос обусловлен обменом молекулами между слоя­ми потока, в турбулентном — обменом объемами. Турбулентный перенос во много раз интенсивнее молекулярного.

Режим движения воздуха в выработке можно определить визу­ально, например, при помощи тонких струек дыма: если струнки сохраняются па значительном расстоянии от источников — движе­ние ламинарное, быстрое их перемешивание с воздухом указывает на турбулентное движение. Определить режим движения воздуха в выработке можно также при помощи специального критерия — числа Рейнольдса Re:

Re = wD/v, (5.18)

где и — средняя скорость движения воздуха в выработке; D — гид­равлический диаметр выработки; v — кинематическая вязкость воз­духа.

Гидравлический диаметр определяется по формуле

D-4S/P, (5.19)

где 5 — площадь поперечного сечения выработки; Р — ее пери­метр. Число Re безразмерно.

60

Экспериментально установлено, что в гладких трубах при Re= = 2300 устойчивым является турбулентное движение, т. е. при этом даже небольшие возмущения потока (внесение в поток посторон­него тела колебания стенки и т. п.) вызывают переход ламинарно­го движения в турбулентное, причем в дальнейшем движение оста­ется турбулентным даже при устранении возмущений. При Re< <2300 устойчиво ламинарное движение.

В шахтных выработках критическое значение числа Re= 1000ч-Ч-1500. Следовательно, минимальная скорость, при которой дви­жение еще остается турбулентным, например при D = 2,5 м и v = = 1,5-10~⁵ м²/с, будет, согласно уравнению (5.67), 0,006—0,01 м/с. Правила безопасности требуют, чтобы скорость движения воздуха в выработках была не менее 0,25 м/с. Фактические скорости дви­жения воздуха в современных шахтах значительно выше. Поэтому в выработках, проветриваемых деятельной вентиляционной струей, движение воздуха, как правило, турбулентное.

При фильтрационном движении воздуха по узким каналам (про­сачивание воздуха через целики, перемычки, уплотненные участки обрушений в выработанном пространстве и т. п.), происходящем обычно при низких скоростях, часто наблюдается ламинарный ре­жим движения.

Переход ламинарного движения в турбулентное в отдельной точке происходит почти мгновенно, однако в пространстве между источником возмущения и сечением потока, где движение турбу­лентное, лежит переходная область, лишь частично заполненная турбулентными вихрями. Наблюдения показывают, что в очень шероховатых воздухопроводах, к которым относится и большин­ство горных выработок, турбулентность зарождается непосредст­венно у выступов шероховатости, в то время как при гладких стен­ках развитие турбулентности может происходить от вихрей, зано­симых ядром потока. Наконец, вдоль потока режим движения мо­жет изменяться вследствие увеличения или уменьшения диаметра канала. Отмеченные обстоятельства приводят к тому, что при дви­жении воздуха возможно существование промежуточных режимов, при которых поток состоит из ряда расположенных по его длине областей с турбулентным и ламинарным режимами *. В шахтных условиях промежуточные режимы наблюдаются, например, при движении воздуха в выработанном пространстве, через слой угля в бункерах, через герметизирующие сооружения.

Однако даже при вполне развитом турбулентном движении у стенок воздухопровода сохраняется тонкий слой (л а м и и а рн ы й пограничный слой), в пределах которого движение лами-нарно. При малых числах Re толщина ламинарного слоя (рис. 22, а) большая и в него оказываются погруженными все вы­ступы шероховатости (или большинство их). При этом они оказы­вают минимальное сопротивление по току. С увеличением числа

* Чередование турбулентного и ламинарного движения в некоторой фикси­рованной точке может происходить также во времени.

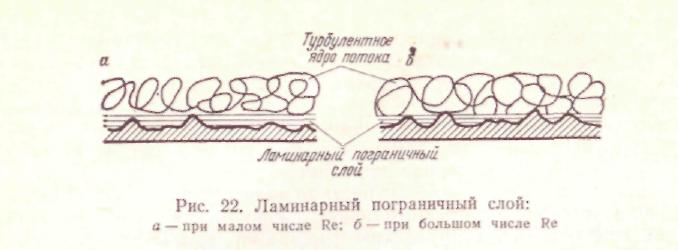
Re толщина ламинарного слоя уменьшается, выступы шерохова­тости внедряются в турбулентное ядро потока, оказывая послед­нему все возрастающее сопротивление (рис. 22,6).

5.4. Типы воздушных потоков в горных выработках

Все воздушные потоки в выработках можно разделить на два основных типа: ограниченные потоки, или потоки с тверды­ми границами, и свободные, не имеющие твердых границ, на­зываемые также свободными струями.

К ограниченным потокам относятся, например, потоки воздуха в штрекообразных выработках на прямолинейных участках при постоянном их сечении. В этом случае потоки имеют твердые гра­ницы в виде стенок выработок.

Свободные струи образуются, когда воздушный поток из воз­духопровода ограниченного сечения выходит в неограниченное (до­статочно большое) пространство. Воздушная струя при этом рас­пространяется в заполненном воздухом пространстве и не имеет твердых границ.

К свободным струям относятся, например, потоки воздуха, вы­ходящие из штрека в камеру большого сечения, из трубопровода в выработку и т. п. В зависимости от формы поперечного сечения свободных струй они могут быть круглыми и плоскими. Если на каком-либо участке свободная струя соприкасается с твердой поверхностью и не получает полного развития, она назы­вается неполной.

Ограниченные потоки и свободные струи движутся по сущест­венно различным законам. Так, в ограниченных потоках происходит падение давления в направлении движения, в свободных же струях давление постоянно и равно давлению окружающего воздуха;^ огра­ниченные потоки имеют логарифмический профиль скоростей, сво­бодные струи—профиль в виде кривой Гаусса; кроме того, эти по­токи различны по характеру протекания диффузионных процессов. Знание законов движения ограниченных потоков необходимо для организации вентиляции выработок типа штреков, квершлагов, лав, а законов движения свободных струй — для организации вен­тиляции камерообразных выработок, призабойной части тупиковых выработок и др.

62

5.5. Закон сопротивления, сопротивление трения горных выработок

Под законом сопротивления в рудничной вентиляции понима­ется зависимость между депрессией h и средней скоростью и (или количеством Q) воздуха в выработке

h = R_lUⁿ = R₂Qⁿ, (5.20)

где Ri и R₂ — коэффициенты пропорциональности; п — показатель степени, зависящий от режима движения; при турбулентном режи­ме /2 = 2; при ламинарном п=\.

В горных выработках при турбулентном режиме движения п=2, при малых скоростях (Rc = 2- 10⁴ч-3- \0*)пж 1.,8.

Механизм действия сил сопротивления. Выше отмечалось, что при движении воздуха в потоке появляются силы трения вследст-

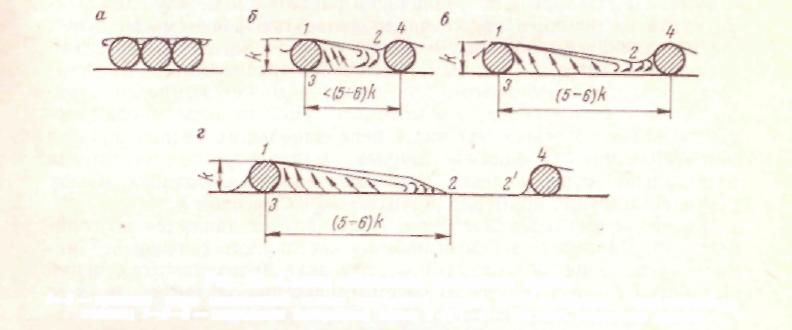
Рис. 23. Схемы обтекания элементов крепи:

1—2 — граница ядра постоянной массы свободной струн; 2—2' — область ограниченного

потока; /—2—3 — застойные (вихревые) зоны; 2 (2')— 4 — область поджатая потока

вие эффекта прилипания и вязкости. Поскольку стенки горных вы­работок шероховаты, движущийся вдоль них воздух оказывает также давление на погруженные в поток выступы шероховатости, вследствие чего появляется вторая составляющая силы сопротив­ления — сила давления. Шероховатость горных выработок обычно относительно равномерно распределена как по их длине, так и по периметру поперечного сечения. В результате силы трения и силы давления распределяются по всей поверхности выработки и везде проявляются совместно. На практике обе силы оценивают совмест­но. Результирующая сила при этом с определенной условностью называется силой трения, а вызываемое ею сопротивление — сопротивлением трения.

В условиях горных выработок основное сопротивление движе­нию воздуха оказывают элементы крепи. Поток воздуха, подойдя к элементу крепи, поджимается (рис. 23), в результате чего лобо­вая часть элемента воспринимает динамическое давление набега­ющего потока. За элементом крепи вследствие срыва потока обра-

63

з уются свободная струя и мертвая зона, заполненная массами воз­духа, находящимися в вихревом движении. Далее в зависимости от расстояния до следующего элемента крепи либо может нахо­диться область ограниченного потока (см. рис. 23, г), либо может вновь начинаться его поджатие (см. рис. 23, а — в). Основными составляющими сопротивления здесь являются давление на лобо­вую часть элемента крепи, диссипация (рассеивание) энергии вследствие трения в вихрях застойной зоны, трения о поверхность крепи и стенки выработки. При сплошном расположении элементов крепи размеры застойных зон минимальны (см. рис. 23,а). По ме­ре увеличения расстояния между элементами крепи увеличивается объем вихревых зон и, следовательно, потеря энергии в них. Одно­временно увеличивается область лобовой крепи, испытывающая давление потока. С появлением участка ограниченного потока (см. рис. 23, г) вихревые зоны достигают наибольшего развития и поте­ря энергии в них, а также силы давления па крепь достигают мак­симума. При дальнейшем увеличении расстояния между элемента­ми крепи их число, а также число полностью развитых вихревых зон на единицу выработки уменьшаются, а сопротивление каждого элемента остается постоянным; увеличение трения о стенки на уча­стках ограниченного потока при этом не может компенсировать снижение сопротивления, вызываемого уменьшением числа эле­ментов крепи. В результате после первоначального увеличения сил сопротивления (на единице длины) до некоторого максимума минимальное сопротивление достигается при расстояниях между элементами крепи, примерно равных 5—6 их высотам к.

Расчет сопротивления трения. Пусть воздух движется по гори­зонтальной прямолинейной выработке постоянного сечения 5. При­меним уравнение Бернулли (5.13) для двух произвольных сечений выработки / — / и // — //. В рассматриваемом случае ii\ = u₂, k_x = = &2> Z\=z₂; при у = const из уравнения (5.13) получим

_Pl—p₂ = h ] dh. (5.21)

(i)

Потерю энергии на преодоление сопротивления между сечения-

ми / — lull — II h — | dh можно выразить через силу трения на

(О единицу длины выработки /:

dh - Tdx, (5.22)

где х — расстояние вдоль потока.

Поскольку dh — работа сил сопротивления (трения) на единицу объема, то Т — сила трения на единицу объема. Тогда очевидно, что

Т = xP./S,, (5.23)

где т — сила трения на единицу площади стенок выработки; Р] — площадь поверхности стенок выработки единичной длины; S] — объем выработки единичной длины.

64

Из уравнений (5.21), (5.22) и (5.23) следует, что

_Pl-~p.₂ = р {rdx/S. (5.24)

(!)

Из курсов гидравлики известно, что

т = рри²/2, (5.25)

где р — безразмерный коэффициент трения, зависящий от широ-ховатости стенок; р—плотность воздуха; и—средняя скорость воздуха в выработке.

Коэффициент р равен отношению энергии Е_тр, теряемой пото­ком в секунду на преодоление сопротивления трения на единице длины выработки, к секундному расходу кинетической энергии по­тока Е_К:

$ = Е^/Е_к = Е^1ри*-2-К

Поскольку при принятых условиях р и и постоянны, принимая шероховатость также постоянной по длине (р = const) и подстав­ляя значение т (5.25) в уравнение (5.24), получим после интегри­рования для депрессии трения

h=.p_x — p« = $pPLu²/2S,

где L — длина выработки между сечениями /—/ и //— //.

Так как p = v/g, u = Q/S, где g— ускорение свободного падения, Q — объемный расход воздуха, то

h = $yPLQV2gS\ (5.26)

Согласно принятым условиям, р и у в пределах рассматривае­мой выработки постоянны. Это позволяет характеризовать их со­вокупное воздействие одной величиной а:

а = f>y/2g_y (5.27)

называемой коэффициентом сопротивления трения. Соотношение между а, р и используемым в гидравлике коэф­фициентом трения I при известных у и g равно

а = 0,6120 = 0,0153?.. (5.28)

С учетом выражения (5.27) формула (5.26) для расчета деп­рессии трения принимает вид

h = aPLQVS³. (5.29)

Из уравнения (5.29) следует, что h зависит от формы попереч­ного сечения выработки, ибо последняя определяет Р при S = const. Величина

R = aPL/S³ (5.30)

называется аэродинамическим сопротивлением тре­ния.

65

3 Зак. 2155

Очевидно, что сопротивление трения единицы длины выработки,, т. е. удельное сопротивление, будет

R'=aP/S³. (5.31)

Из формулы (5.30) следует, что а также выражает удельное сопротивление выработки при такой ее длине, для которой PL/S³ = = 1.

Для круглых воздухопроводов диаметром D /z = 6,48a(L/D⁵)Q², R = 6,48aL/£)⁵ ж 6,5aL/Z)⁵. (5.32)

Формулы (5.29) и (5.30), как следует из принятых допущений, в полной мере справедливы для прямых выработок постоянного сечения и постоянной шероховатости, при постоянной плотности воздуха, средней скорости и вполне развитом турбулентном режи­ме его движения в выработке.

Если плотность воздуха в выработке переменна, приведенные выше формулы для расчета депрессии становятся неприемлемыми, поскольку они получены интегрированием уравнения (5.24) при р = const и выражают потерю энергии, отнесенную к единице объе­ма воздуха, количество материи в котором вследствие непостоян­ства плотности также переменно по длине выработки. Поэтому при р = ]/аг следует оперировать энергией, отнесенной к единице массы, расход которой по длине не меняется. По Б. И. Медведеву, «депрессия по массе»

h! = pPLG²/2p2_pS³, (5.33)

где р_Ср — средняя плотность воздуха в выработке; G — массовый расход воздуха.

Коэффициент сопротивления трения. Из уравнения (5.30) вид­но, что единственной величиной, требующей специального исследо­вания для надежного определения сопротивления трения, является коэффициент трения а. Изучением его длительное время занимался ряд отечественных и зарубежных ученых.

В результате исследований было установлено, что величина а в общем случае зависит от числа Re потока и шероховатости сте­нок выработки.

Зависимость а от числа Re потока определяется зависимостью безразмерного коэффициента трения ?»(р) от Re. Как видно из рис. 24, при увеличении числа Re (скорости потока) вначале коэф­фициент трения уменьшается по гиперболе />. = 64/Re (закон Гаге-на — Пуазейля) и не зависит от шероховатости стенок. Закон Гагена — Пуазейля справедлив для ламинарного движения. По мере развития турбулентности потока с увеличением Re уменьше­ние коэффициента /. вначале замедляется, а затем начинается его рост. Последнее объясняется уменьшением толщины ламинарного пограничного слоя потока и внедрением выступов шероховатости в его турбулентное ядро.

Из рис. 24 и 25 видно, что , начиная с определенного значения

66

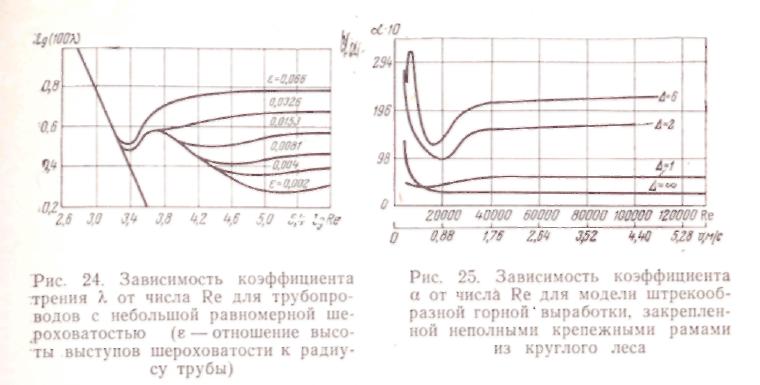
числа Re, величина а остается примерно постоянной *. Это явление называется автомодельностью коэффициента а от­носительно числа Re. Оно наступает в условиях вполне раз­витого турбулентного режима, т. е. при больших числах Re. Для торных выработок автомодельность наступает при Re> (0,5-ь 1) • 10⁵, что соответствует гидравлическому диаметру 2,5 м и ы^0,3 м/с. Эти условия характерны для большинства выработок с активной вентиляционной струей. Поэтому при практических расчетах при­нято считать, что коэффициент а не зависит от числа Re (скорости) потока. Однако при весьма малых его скоростях зависимость (5.27) может оказаться существенной.

Зависимость а от шероховатости стенок выработки видна из ■формулы (5.27). Многочисленные исследования позволили заклю­чить, что на величину а влияет как степень, так и характер шеро­ховатости стенок выработки.

Степень шероховатости характеризуется отношением высоты ее выступов k к гидравлическому диаметру D (радиусу)

(5.34)

е = k/D,

называемым относительной шероховатостью.

Увеличение а при увеличении числа Re начинается тем раньше, чем больше е (см. рис. 23). В воздухопроводах с большой относи­тельной шероховатостью автомодельность наступает раньше; осо­бенно это относится к горным выработкам.

Из выражения (5.34) следует, что, поскольку е зависит от ди­аметра выработки D, коэффициент трения зависит и от площади .ее поперечного сечения. В этом случае влияние площади сечения сводится к изменению относительной шероховатости. Для встре-

* Данные М. М. Ольвовского.

3* 67

чающегося в горной практике диапазона изменения 5 величина а может изменяться до полутора раз.

Поскольку шероховатость выработки образуется чередующими­ся по ее длине элементами крепи, можно ожидать существенного влияния на а продольной плотности расположения этих элементов, которая характеризуется продольн ы м к а л и б р о м креп и:

А = Ilk,

где / — расстояние между осями соседних элементов крепи.

Как показали многочисленные эксперименты (рис. 26), макси­мум а наблюдается при Д = 4-^6.

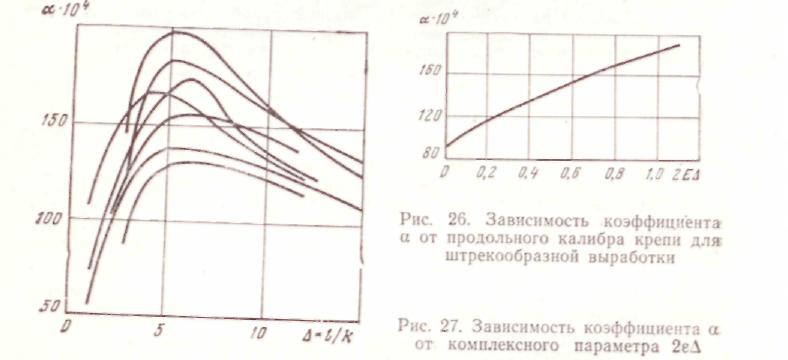
Совокупное влияние е и Д на величину коэффициента а видно из рис. 27. Кроме перечисленных факторов, на коэффициент трения влияет изменение удельной массы воздуха [см. уравнение (5.27)], например в глубоких шахтах, при пожарах и др.

5.6. Методы определения коэффициента аэродинамического сопротивления горных выработок

Существуют два метода определения коэффициента аэродина­мического сопротивления — аналитический и экспериментальный.

Экспериментальный метод заключается в следующем. Выби­рают прямолинейный участок выработки длиной L=l00 м и с по­мощью микроманометра и воздухомерных трубок, подсоединенных к резиновым шлангам и установленных в начале и конце выбран­ного участка выработки,"определяют депрессию h. Затем измеряют площадь поперечного сечения S и периметр Р выработки. С по­мощью анемометров или микроманометра и воздухомерных тру­бок определяют скорость движения воздуха в сечениях выработки, между которыми измеряется депрессия. По известным скорости

68

движения воздуха и и площади поперечного сечения выработки S определяют расход воздуха Q (м³/с):

Q = S«_cp.

Определив все необходимые значения, находят коэффициент аэродинамического сопротивления горной выработки

а = hS^s/PLQ\ (5.36)

Для аналитического определения этого коэффициента произво­дится расчет по предложенной В. Н. Ворониным зависимости:

а = Ща + Ы/Р, (5.37)

где а и Ь — эмпирические коэффициенты, подлежащие эксперимен­тальному определению для каждого вида крепи.

Значения а зависят от конкретных условий в горных выработ­ках.

Снижение коэффициента трения. Любые мероприятия, умень­шающие шероховатость выработок, способствуют снижению значе­ния а. Наиболее эффективными среди них являются:

для незакрепленных выработок — торкретирование стенок, по­крытие их рифленым железом, применение пластмассовых покры­тий (при этом а снижается в 2—4 раза);

для выработок с бетонной и кирпичной крепью — тщательная штукатурка стен (а снижается в 2 раза);

для выработок с рамной крепью — обшивка крепи досками, за­тяжка породных стенок между рамами деревом или бетонными плитами, заполнение пространства, между рамами чурками, изме­нение продольного калибра крепи, заполнение углублений балок.

При увеличении площади сечения выработки а снижается вслед­ствие уменьшения относительной шероховатости выработки.