Примеры построения плана скоростей

Пример 1.

Построить план скоростей для кривошипно-шатунного механизма (рис.6а).

Дано: размеры звеньев, угловая скорость ведущего звена , положение ведущего звена .

Определить скорость точек А, В, С и угловую скорость звена 2.

1. Выбираем масштабный коэффициент плана положения механизма и вычерчиваем методом засечек кинематическую схему механизма в заданном положении кривошипа.

2. Выбираем полюс плана скоростей .

3. Кривошип 1 совершает простое вращательное движение, при заданном положении кривошипа скорость точки А известна по величине –

и направлению – перпендикулярно звену АВ, в сторону вращения кривошипа (рис.6б).

Откладываем из полюса отрезок , изображающий скорость и определяем масштабный коэффициент скоростей:

4. Шатун 2 совершает плоскопараллельное движение, поэтому для точки В запишем уравнение:

Скорость т.А известна во величине и направлению (подчеркнем двумя чертами ). Скорость т.В относительно т.А известна только по направлению – перпендикулярна радиусу вращения (подчеркнем одной чертой и отметим, что ).

С другой стороны, т.В принадлежит ползуну 3, совершающему поступательное движение, поэтому направление движения т.В известно – вдоль направляющей . Подчеркиваем одной чертой и отмечаем, что .

Графически решаем данное векторное уравнение: из конца вектора (точка a на плане скоростей) проводим прямую, перпендикулярную АВ, а из полюса проводим линию, параллельную . На пересечении этих линий ставим т.в. Отмечаем направление относительной скорости , которая изображается вектором и абсолютной скорости (вектор на плане). Определяем их величины:

5. Для определения скорости т. С применим теорему подобия. На векторе плана скоростей построим треугольник 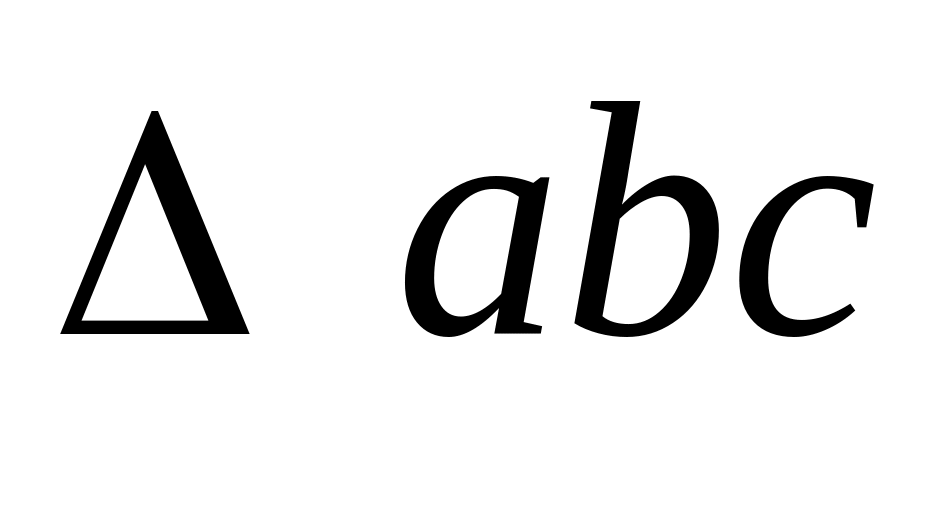подобный 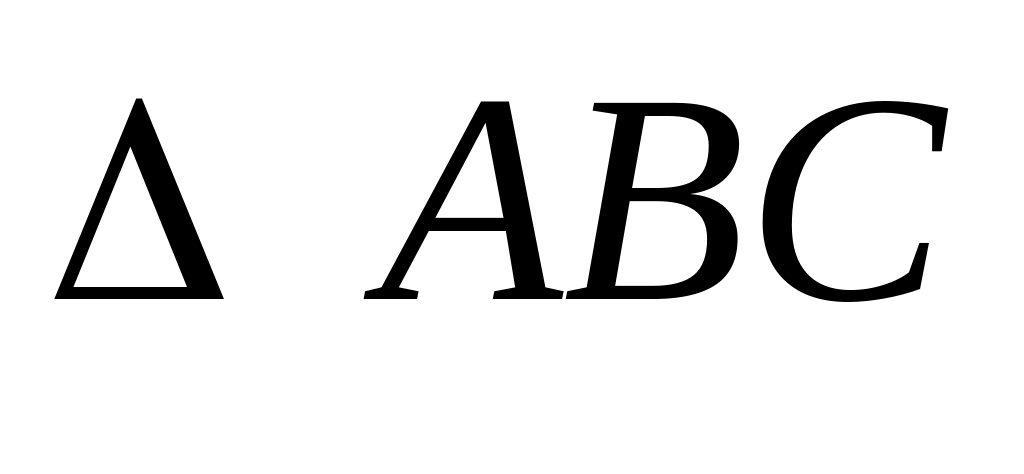, соблюдая правило обхода контура.

Для построения подобных треугольников ~ из т.а плана скоростей проводим прямую , а из т.в – прямую . В пересечении этих линий получаем т.с, которая определяет конец вектора скорости т.С , начало которого находится в полюсе. Величина скорости т.С определяется:

6. Определяем угловую скорость шатуна 2 по формуле:

Для определения направления перенесем вектор в т.В плана механизма. Как видно из чертежа, создает вращение шатуна вокруг т.А по часовой стрелке. Угловая скорость направлена по часовой стрелке.

Пример 2

Построить план скоростей для кривошипно-коромыслового механизма (рис.7а).

Д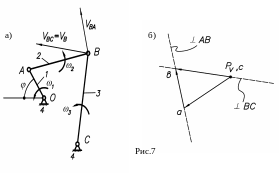 ано: размеры звеньев, угловая скорость ведущего звена , положение ведущего звена . Определить скорость точек А, В и угловые скорости звеньев 2 и 3.

Вычерчиваем механизм в заданном положении.

1. Определяем скорость т. А:

Скорость т. А направлена в сторону вращения кривошипа. От полюса откладываем вектор , изображающий скорость т. А.

Определяем масштабный коэффициент скоростей:

2. Определяем скорость т. В. (рис.7б).

Точка В принадлежит двум звеньям – шатуну 2 и коромыслу 3.

Шатун совершает плоскопараллельное движение, поэтому запишем

Коромысло совершает вращательное движение вокруг т. С, поэтому запишем:

Графически решаем систему уравнений:

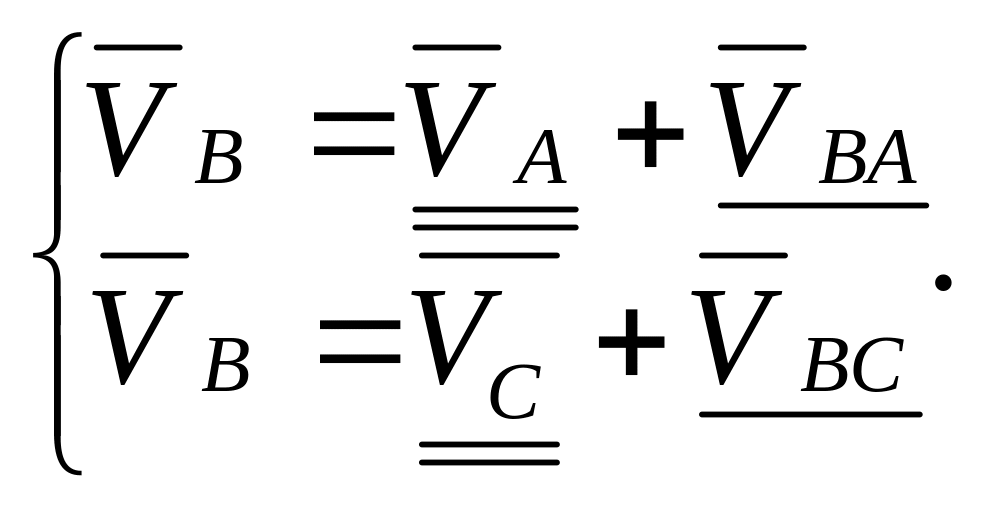
Решаем первое уравнение. Из конца вектора – т. а проводим прямую, перпендикулярную звену АВ. Решаем второе уравнение. Скорость т. С равна нулю. Помещаем т. с в полюс плана скоростей. Из полюса проводим прямую, перпендикулярную ВС.

В пересечении двух линий действия скоростей получаем точку в. Вектор определяет искомую скорость:

3. Определяем угловые скорости звеньев.

Угловая скорость шатуна:

Направление определяем по направлению вектора относительной скорости перенесенного в т. В плана механизма. Как видно из рис.7б, вектор определяет направление вращения шатуна против часовой стрелки.

Угловая скорость коромысла:

По направлению скорости определяем направление – против часовой стрелки.

Пример 3

Построить план скоростей для кулисного механизма (рис.8а).

Дано: размеры звеньев, угловая скорость ведущего звена , положение ведущего звена .

1. Звено 1 вращается вокруг т. О с угловой скоростью , поэтому:

Скорость т. А₁ направлена в сторону вращения кривошипа. От полюса в масштабе откладываем вектор , изображающий скорость т. А₁ (рис.8б).

Точка А₁ тождественна точке А₂ (в противном случае не было бы передачи движения), А₁ = А₂. Следовательно,

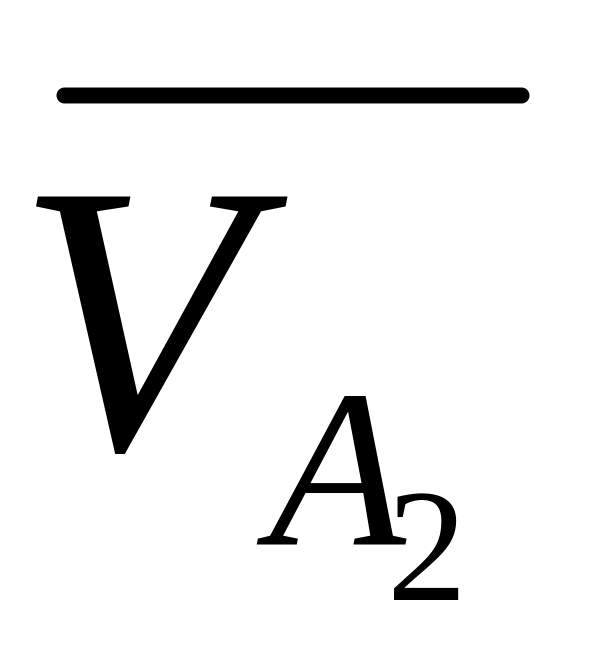2. Вектор определен по величине и направлению. С одной стороны, точка А₂ совершает вращательное движение относительно точки О (стойки механизма). С другой стороны, точка А₂ совершает поступательное движение относительно кулисы (звено 5) и вращательное движение вместе с кулисой вокруг точки В.

Таким образом, точка А₂ совершает сложное движение. Абсолютное движение – движение точки А₂ относительно неподвижной системы координат (стойки механизма), относительное движение – поступательное движение точки А₂ относительно кулисы (относительно точки А₃) и переносное движение – вращательное движение кулисы (точки А₃) вокруг центра В (стойки механизма).

Для того, чтобы получить величины скоростей и , направление которых известно, вектор абсолютного движения необходимо разложить на две составляющие по направлениям векторов и . Иными словами, можно записать уравнение:

где - вектор скорости т. А₂ в абсолютном движении;

- вектор скорости т. А₃ в переносном движении, т.е.

- переносная скорость кулисы 3;

- относительная скорость движения т. А₂ относительно А₃ или

скорость ползуна 2 по кулисе 3. .

Т очка В принадлежит стойке механизма, поэтому .

Согласно уравнению: - вектор скорости т. А₂ является результирующим вектором, отложенным на плане скоростей как вектор , поэтому к результирующему вектору пристраиваем два суммируемых вектора – и . Для этого из начала вектора (с учетом уравнения ) из т. – полюса плана скоростей – проводим линию перпендикулярно ВС (направление скорости т.А₃ относительно т. В). Линию действия относительной скорости проводим из конца вектора – от точки . Пересечение указанных линий действия определит точку – конец вектора . Вектор будет представлять собой скорость скольжения . Находим модули скоростей:

3. Используя частный случай теоремы подобия, определим отрезок , изображающий скорость точки С. Запишем соотношение:

4. Скорость т.D определяется из уравнения:

После решения этого уравнения получаем:

5. Определение угловых скоростей звеньев 3 и 4. Угловая скорость кулисы 3 определяется соотношением:

и направлена по часовой стрелке (по направлению скорости V_А3), аналогично:

– по часовой стрелке.

ПОСТРОЕНИЕ ПЛАНА УСКОРЕНИЙ