6.09.2012

Тема: «Представление информации»

Любое практическое исследование на начальном этапе включает стадию сбора информации. Для изучения предмета или объекта необходимо систематизировать данные. Для обобщения необходимо выделять совокупности общих или различных свойств объектов. Такие свойства называются признаками. Признаки бывают:

1. Детерминированные

2. Логические

3. Вероятностные

4. Структурные

Одним из универсальных представлений является табличное. Чтобы извлечь информацию необходимо представить данные в виде модели. Модель – абстрактное представление данных с целью улучшения интерпретации.

Виды моделей:

• Математическая

• Физическая

• Информационная

Классификация моделей:

1. Гипотеза (какое могло бы быть).

2. Феноменологические модели (если бы это произошло)

3. Информационные модели рассматривают объекты в виде «черного ящика» с входящим и выходящим

4. Упрощения (опустим для ясности некоторые детали)

5. Эвристическая модель (подтверждений нет, но модель позволяет понять суть)

6. Аналогия (учтём особенности предыдущего опыта)

7. Мысленный эксперимент (состоит в опровержении возможностей)

8. Демонстрация возможности (показать внутреннее непротиворечие)

Типы шкал признаков:

1. Непрерывная шкала – признаки могут принимать любые вещественные значения.

2. Дискретные шкалы – признаки не являются вещественными:

• Номинальные шкалы – применяются если число не является выражением какой-то меры а служит меткой варианта ответа на вопрос.

• Порядковые – целое число отражает степень проявление определённого качества (степень уверенности).

При представлении и обработке данных необходимо учитывать :

1. Не всегда признаковые таблицы полные (неопределённые данные)

2. Значение признаков измеряется с определенной точностью.

3. Данные допускают отклонения (данных)

Представление данных

Для представления данных часто используется признаковое геометрическое пространство.

	X1	X2
01	10	20
02	11	22
03	20	5
…	23	7

В таком пространстве объекты представляются точкой, координаты которой являются значениями признаков. Если есть допустимость, то вместо точки изображаем геометрическую фигуру.

Классом называют область в признаковом пространстве, объединённая схожестью свойствами объектов.

Пример формального анализа

	Признак	Правило	Класс
Решение анализа	+	+	+
Классификация	+	?	+
Кластеризация сегментация	+	+	?
Информатизация признакового пространства	?	+	+

Для построения правила решений вводится понятие метрики пространства. Метрические пространства должны удовлетворять следующим свойствам:

1. Метрика должна быть положительна

2. Симметрична

3. Метрика равна 0, если объекты совпадают (A=B)

4. Для того чтобы величина была метрикой необходимо

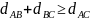
13.09.2012

Тема: «Статистическая обработка данных»

Параграф: Основные сведенья из теории вероятности.

Случайное событие – событие, которое может произойти и может не произойти. Существует достоверное и невозможное событие.

A, B, C – обозначение случайных событий.

Случайные событие бывают совместные и несовместные (наступление одного исключает события другого). Противоположные событие в группе составляют достоверное событие (например: подбросить монету).

Полная группа – это попарно несовместные события, которые вместе составляют достоверные события.

Алгебра событий:

Сумма событий -> C=A+B -> заключает в себе события и A и B.

Произведение событий -> C=AB -> произойдет и событие A и событие B.

Классическое определение вероятностей:

-> n- общее количество, m – благоприятствующие события.

C=A+B -> – если они не совместны.

C=A+B -> – если они не зависимы

– при условии, что событие А уже произошло.

Формула полной вероятности (формула Байеса):

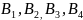
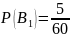
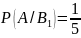
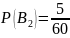
– вероятность того, что студент сдавший экзамен будет с группы с плохой посещаемостью.

Случайная величина – определяет:

1. Отношение строгого порядка, введенного на множестве элементарных событий.

2. Вероятностью того, что это случайная величина примет конкретное значение.

	1	2	3	4	5	6

- для кубика.

	1	2

- для монеты.

Если случайная величина может принять любое значение из диапазона, тогда она называется аналоговой (или непрерывная).

– это функция, полученная как попадание случайной величины в бесконечно малый интервал.

Функция распределения ->

Пример:

	1	2	3	4	5	6

– не бывает грани меньше единице.

Для нахождения функции:

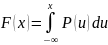
Числовые характеристики случайных величин делятся на три группы:

1. Центра группирования

2. Разбросы или вариации.

3. Статистические связи.

20.09.2012.

Числовые характеристики центра группирования:

1. Среднее арифметическое или математическое ожидание – если величина дискретная, то мы можем найти значение просуммировав все результаты и разделив на количество – базовая формула нахождения математического ожидания.

Для непрерывной случайной величины

2. Мода – применяются в случае, если закон распределения мультимодален и эти точки наибольшей вероятности. .

3. Медиана – используя полученные данные в порядке возрастания. В качестве результата обработки используем результат расположенный посередине. 1,6 1,85 1,75 5,4 1,7 1,6 1,7 1,75 1,85 5,4 ... …

Физический смысл – вероятность того, что величина будет меньше этого значения, равна вероятности появления большего значения.

Квантиль уровня 0,9 – это значение в точке распределения 0,9 (Графически).

4. Для разрешения мультипликативного фактора мы логарифмируем значение закона распределения. (?)

5. Дисперсия – характеризует разброс значений распределения.

6. Среднеквадратическое отклонение - .

Числовые характеристики …

X – случайная величина рост.

Y – случайная величина вес.

– значение отклонения

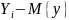– значение отклонения

Ковариация -

Нормирование -

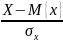
Коэффициент корреляции - .

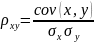Закон больших чисел

При достаточно большом количестве испытаний, математическое ожидание приближается к среднему значению вероятности.

X1, X2, …, Xn – закон распределения среднего арифметического не зависит от законов распределения каждого значения распределения.

(Центральная предельная теорема)

4.10.2012