Контрольные вопросы и задания:

1. Что называют растворами полимеров ?

2. По какому признаку растворители полимеров делят на «хорошие» и «плохие»?

3. Каким путем фиксируют форму материалов и изделий, получаемых из растворов полимеров ?

4. Происходит ли фазовое разделение растворов полимеров при получении из них каких-либо материалов методом высушивания при повышенных температурах ?

5. Происходит ли фазовое разделение растворов полимеров при фиксации приданной им формы в осадительной ванне ?

6. Каковы достоинства и недостатки метода переработки полимеров через растворы ?

7. Расскажите порядок выполнения лабораторной работы.

8. «Хороший» или «плохой» растворитель использован в лабораторной работе для приготовления раствора полимера ?

9. Какое вещество использовано в лабораторной работе в качестве осадителя полимера ?

10. Пористую или непористую структуру имеют пленки, получаемые в лабораторной работе путем высушивания раствора полимера ?

11. Пористую или непористую структуру имеют пленки, получаемые в лабораторной работе путем фазового разделения раствора полимера в осадительной ванне ?

12. Что происходит с раствором полимера при помещении его в осадительную ванну ?

Лабораторная работа № 5

РЕЛАКСАЦИОННЫЕ СВОЙСТВА ПОЛИМЕРОВ

Цель работы. Ознакомление студентов с релаксационными свойствами полимеров на примере ползучести и упругого восстановления сырых резиновых смесей и вулканизованных резин.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Релаксационные свойства полимеров

Общие положения. Полимерные тела или системы всегда стремятся перейти в такое состояние, в котором их параметры не изменяются во времени. Такое состояние называется статистически равновесным или просто равновесным. Достигнув его, тело или система будет находиться в равновесии до тех пор, пока не будут изменены условия, в которых оно находится.

Любое изменение условий (появление растягивающих усилий, изгиб, нагрев, обработка лучами с высокими энергиями, снятие когда-то приложенного напряжения и т.п.) приводит к тому, что состояние, бывшее равновесным в прежних условиях, в новых условиях оказывается неравновесным. Оказавшись в неравновесном состоянии, вследствие теплового движения составляющих элементов тело или система стремится вновь перейти в равновесное состояние, но уже отвечающее изменившимся условиям. Если вновь изменить условия, то тело или система вновь будет переходить в равновесное состояние. Таким образом, условия могут изменяться бесконечное число раз и каждый раз полимерное тело или система будет стремиться перейти в равновесное состояние, отвечающее тем условиям, в которых оно находится в данный момент.

Этот происходящий во времени переход тела или системы из неравновесного состояния в равновесное называется релаксацией (от английского слова relax – ослаблять).

Из всех релаксационных явлений в полимерах наиболее важными являются механические явления, а из них ползучесть (или крип) – изменение во времени деформации тела или системы при постоянно действующем напряжении и упругое восстановление (или упругое последействие) – изменение во времени деформации тела или системы после снятия ранее приложенной нагрузки.

Напряжение, деформация. Напряжение – это отношение силы F, приложенной к некоторой площадке тела, к площади этой площадки S. В зависимости от вида нагружения различают напряжения нормальные (обозначаемые буквой σ), если сила прикладывается перпендикулярно выбранной площадке, и касательные (обозначаемые буквой τ), если сила действует вдоль площадки (по касательной к ней).

Под действием напряжений в телах могут развиваться деформации. Деформация – это относительное изменение расстояния между двумя произвольно выбранными точками тела.

Всего существует три вида деформаций полимеров:

- мгновенная упругая;

- высокоэластическая;

- пластическая (она же – вязкого течения, вязкотекучая).

Мгновенная упругая деформация обусловлена изменением валентных углов и межатомных расстояний в макромолекулах:

ι

ι+ι₁

ι

α

α+β

α

Макромолекула в Макромолекула под Макромолекула по-

исходном состоянии напряжением сле снятия напряжения

Рис. 1. Проявление мгновенной упругой деформации.

Мгновенная упругая деформация возникает со скоростью звука при приложении нагрузки и с такой же скоростью исчезает после ее снятия, т.е. практически мгновенно. Полностью обратима. По величине невелика: по некоторым данным – до 5-7 %.

Высокоэластическая деформация обусловлена изменением конформаций макромолекул:

Макромолекула Макромолекула под Макромолекула

в исходном напряжением после снятия

состоянии напряжения

Рис. 2. Проявление высокоэластической деформации.

Высокоэластическая деформация возникает и постепенно развивается во времени при приложении нагрузки. После снятия нагрузки постепенно восстанавливается. Полностью обратима. Характерна для аморфных полимеров. Может достигать от нескольких процентов до многих сотен процентов. Наиболее ярко проявляется при механических воздействиях на эластомеры.

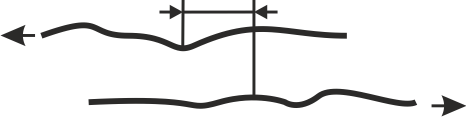
Пластическая деформация обусловлена перемещением макромолекул относительно друг друга.

а

b

b

Макромолекулы Макромолекулы под Макромолекулы

в исходном напряжением после снятия

состоянии напряжения

Рис. 3. Проявление пластической деформации.

Пластическая деформация возникает и постепенно развивается во времени при приложении нагрузки. После снятия нагрузки остается без изменений, т.е. необратима. В зависимости от температуры, величины нагрузки, структуры полимера, времени выдержки под нагрузкой и некоторых других факторов пластическая деформация может вообще не проявляться, а может достигать очень больших значений.

Если в процессе испытания полимер проявляет все три вида деформаций, то в любой момент времени его общая деформация представляет собой их сумму:

ε_общ. = ε_мгн.у + ε_вэ + ε_пл

Если же полимер не проявляет какой-то вид деформации, то из этого уравнения удаляется соответствующее слагаемое.

Механические модели. Перед изучением ползучести и упругого восстановления полимеров рассмотрим механические модели, позволяющие изучать ползучесть и упругое восстановление отдельных типов тел.

Рассмотрим поведение:

1. Модели идеального упругого тела.

2. Модели ньютоновской вязкой жидкости.

3. Модели простейшего вязкоупругого твердого тела.

4. Модели простейшего вязкоупругого жидкого тела.

5. Модели сложного вязкоупругого тела.

Испытания всех моделей проводят одним и тем же способом: к модели на какое-то время подвешивают груз и наблюдают за изменением возникшего в ней напряжения и развиваемой в ней деформации, затем, по истечении выбранного времени, груз снимают и вновь наблюдают за изменением напряжения и деформации.

При таком виде испытаний характер зависимости напряжения от времени для всех рассматриваемых моделей имеет один и тот же вид (рис. 4): в момент приложения нагрузки напряжение мгновенно достигает какого-то значения, достигнув его, остается неизменным весь период времени выдерживания модели под нагрузкой и мгновенно исчезает после снятия нагрузки.

Рис. 4. Режим нагружения моделей.

О – момент приложения нагрузки;

А – момент снятия нагрузки.

Характер изменения деформации во времени зависит от вида рассматриваемой модели.

1. Модель идеального упругого тела.

Моделью идеального упругого тела является упругая пружина (рис. 5). При ее нагружении вся затраченная на растяжение энергия мгновенно накапливается в виде упругого потенциала. После снятия нагрузки вся запасенная энергия мгновенно расходуется на возвращение пружины в исходное состояние.

Строение модели предопределяет следующий характер развития в ней деформации (рис. 5): в момент приложения нагрузки деформация мгновенно достигает какого-то значения, достигнув его, остается неизменной весь период времени выдерживания модели под нагрузкой и мгновенно исчезает после снятия нагрузки.

Такой характер зависимости деформации от времени свидетельствует о том, что деформация, развиваемая в модели, полностью обратима и что переходы из неравновесного состояния в равновесное осуществляются этой моделью практически мгновенно.

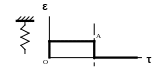
Рис. 5. Зависимость деформации модели идеального

упругого тела от времени ее нагружения и отдыха.

О – момент приложения нагрузки;

А – момент снятия нагрузки.

Можно отметить, что такой же вид имеют кривые испытаний тех реальных полимеров, которые при используемых нагрузках проявляют только мгновенную упругую деформацию. К таким полимерам можно отнести полимеры, находящиеся в стеклообразном или высококристаллическом состоянии.

2. Модель ньютоновской вязкой жидкости.

Моделью ньютоновской вязкой жидкости является шарик в вязкой жидкости (рис. 6). Эта модель не способна запасать энергию деформирования: при нагружении вся энергия, затрачиваемая на перемещение шарика, превращается в тепло и рассеивается в пространстве (диссипирует).

Строение модели предопределяет следующий характер развития в ней деформации (рис. 6): с момента приложения напряжения деформация постоянно, прямолинейно увеличивается; после снятия нагрузки ее величина не изменяется, а остается на достигнутом уровне.

Такой характер зависимости деформации от времени свидетельствует о том, что развиваемая в модели деформация необратима и что в любой момент времени (и под нагрузкой и после ее снятия) модель находится в равновесном состоянии.

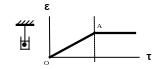
Рис. 6. Зависимость деформации модели ньютоновской

вязкой жидкости от времени ее нагружения и отдыха.

О – момент приложения нагрузки;

А – момент снятия нагрузки.

Такой же вид имеют кривые испытаний тех реальных полимеров, которые при используемых нагрузках и скоростях нагружения проявляют только пластическую деформацию.

3. Модель простейшего вязкоупругого твердого тела.

Моделью простейшего вязкоупругого твердого тела является система, состоящая из параллельно соединенных модели идеального упругого тела и модели ньютоновской вязкой жидкости (рис. 7). При ее нагружении часть энергии, затрачиваемой на растяжение, постепенно накапливается пружиной в виде упругого потенциала, а часть рассеивается в пространстве при перемещении шарика в вязкой жидкости. После снятия нагрузки из всей запасенной пружиной энергии одна часть расходуется на постепенное возвращение системы в исходное состояние, а другая часть рассеивается в пространстве в процессе перемещения шарика в вязкой жидкости.

Строение рассматриваемой модели предопределяет следующий характер развития в ней деформации (рис. 7): при приложении нагрузки деформация сначала быстро, а затем все медленнее (мешает шарик в вязкой жидкости) нарастает и по истечении какого-то промежутка времени становится постоянной (пружина больше не растягивается). После снятия нагрузки деформация сначала быстро, а затем все медленнее (мешает шарик в вязкой жидкости) убывает и по истечении какого-то промежутка времени полностью исчезает (пружина привела систему в исходное состояние).

Такой характер зависимости деформации от времени свидетельствует о том, что развиваемая в модели деформация полностью обратима и что переходы из неравновесного состояния в равновесное осуществляются этой моделью постепенно, во времени.

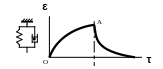
Рис. 7. Зависимость деформации модели простейшего

вязкоупругого твердого тела от времени ее нагружения и отдыха.

О – момент приложения нагрузки;

А – момент снятия нагрузки.

Можно отметить, что такой же вид имеют кривые испытаний тех реальных полимеров, которые при используемых нагрузках проявляют только высокоэластическую деформацию. К таким полимерам можно отнести пространственно сшитые полимеры, находящиеся в высокоэластическом состоянии.

4. Модель простейшего вязкоупругого жидкого тела.

Моделью простейшего вязкоупругого жидкого тела является система, состоящая из последовательно соединенных модели идеального упругого тела и модели ньютоновской вязкой жидкости (рис. 8). При ее нагружении часть энергии, затрачиваемой на растяжение, мгновенно накапливается пружиной в виде упругого потенциала, а часть рассеивается в пространстве в процессе движения шарика в вязкой жидкости. После снятия нагрузки та часть энергии, которая была запасена пружиной, расходуется на ее мгновенное сокращение.

Строение данной модели предопределяет следующий характер развития в ней деформации (рис. 8): в момент приложения нагрузки деформация мгновенно достигает какого-то значения (срабатывает пружина) и, достигнув его, постепенно, прямолинейно увеличивается (перемещается шарик в вязкой жидкости). После снятия нагрузки мгновенно исчезает деформация, вызванная растяжением пружины, а деформация, вызванная смещением шарика, остается без изменений.

Такой характер зависимости деформации от времени свидетельствует о том, что развиваемая в модели деформация обратима не полностью и что переходы из неравновесного состояния в равновесное осуществляются моделью практически мгновенно.

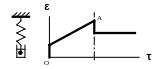
Рис. 8. Зависимость деформации модели простейшего

вязкоупругого жидкого тела от времени ее нагружения и отдыха.

О – момент приложения нагрузки;

А – момент снятия нагрузки.

Можно отметить, что такой же вид имели бы кривые испытаний реальных полимеров, если бы они проявляли только мгновенную упругую и пластическую деформации.

5. Модель сложного вязкоупругого тела.

Моделью сложного вязкоупругого тела является система, состоящая из трех последовательно соединенных моделей: модели идеального упругого тела, модели простейшего вязкоупругого твердого тела и модели ньютоновской вязкой жидкости (рис. 9). При ее нагружении из всей энергии, затрачиваемой на растяжение, одна часть накапливается в виде упругого потенциала пружинами, а другая рассеивается в пространстве в процессе перемещения шариков в вязких жидкостях. После снятия нагрузки часть энергии, запасенной пружинами, возвращает их в исходные положения, а часть рассеивается в пространстве при перемещении шариков в вязких жидкостях.

Строение модели предопределяет следующий характер развития в ней деформации (рис. 9): при приложении нагрузки деформация развивается сначала мгновенно (мгновенно растягивается верхняя пружина), затем скорость ее развития постепенно замедляется (быстрому растягиванию второй пружины мешает расположенный параллельно с ней шарик в вязкой жидкости) и по истечении какого-то промежутка времени она начинает увеличиваться прямолинейно (обе пружины растянуты и больше не растягиваются, но движется нижний шарик в вязкой жидкости). После снятия нагрузки деформация мгновенно уменьшается на ту же величину, на которую мгновенно увеличилась при приложении нагрузки (мгновенно сжимается верхняя пружина), затем скорость ее уменьшения постепенно замедляется и по истечении какого-то промежутка времени деформация достигает постоянного значения (закончила сжиматься вторая пружина, а деформация, которую проявил нижний шарик в вязкой жидкости, осталась без изменений).

Такой характер зависимости деформации от времени свидетельствует о том, что развиваемая деформация обратима не полностью и что переходы из неравновесного состояния в равновесное осуществляются рассматриваемой моделью во времени.

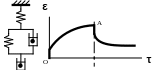
Рис. 9. Зависимость деформации модели сложного

вязкоупругого тела от времени ее нагружения и отдыха.

О – момент приложения нагрузки;

А – момент снятия нагрузки.

Такой же вид имеют кривые испытаний тех реальных полимеров, которые при используемых нагрузках проявляют все три вида деформации: мгновенную упругую, высокоэластическую и пластическую. К таким полимерам в первую очередь можно отнести эластомеры, не имеющие пространственно сшитой структуры.

Ползучесть и упругое восстановление реальных полимерных тел (рис. 10). При приложении нагрузки в полимерах сразу же развивается мгновенная упругая деформация (на кривой ей соответствует участок ОС), затем постепенно начинает развиваться высокоэластическая деформация и одновременно с ней пластическая (на кривой это участок СА). После снятия нагрузки начинается процесс упругого восстановления. Вначале быстро восстанавливается мгновенная упругая деформация (на кривой это участок АВ, по величине равный отрезку ОС), затем постепенно восстанавливается высокоэластическая деформация вплоть до некоторых значений остаточной деформации (ε_ост.).

Величина и состав этой деформации определяются свойствами полимерного тела и временем наблюдения. Чаще всего в состав остаточной деформации входят пластическая деформация и та часть высокоэластической деформации, которая не отрелаксировала к моменту окончания эксперимента из-за того, что протекает с малой скоростью:

ε_ост. = ε_пл + ε_вэ

Если же к моменту окончания эксперимента релаксация полимера прошла полностью (ε_вэ = 0), то остаточная деформация – есть ничто иное как пластическая деформация. Если в процессе испытания полимер не проявил пластическую деформацию (ε_пл = 0), то в этом случае остаточную деформацию составляет только высокоэластическая деформация.

Следует отметить, что релаксация полимеров – это, как правило, достаточно длительный процесс и быстро определить закончился ли он, не всегда представляется возможным. Ускорить релаксацию можно путем нагревания образца, выдержки его в растворителе или в парах растворителя, обработки токами высокой частоты или иным каким-либо способом.

Рис. 10. Ползучесть и упругое восстановление

полимера в высокоэластическом состоянии.

О – момент приложения нагрузки;

А – момент снятия нагрузки.

Можно также отметить, что кривая, приведенная на рис. 10, наиболее характерна для несшитых полимеров, находящихся в высокоэластическом состоянии. Для полимеров, находящихся в стеклообразном или в высококристаллическом состоянии, для сшитых полимеров, термоэластопластов, соотношения между проявляемыми деформациями другие, из-за чего кривые испытаний имеют иной вид.

Рассматривая характер развития деформации полимеров в процессе их ползучести и упругого восстановления можно отметить, что, если при упругом восстановлении релаксация полимера прошла не полностью, то по результатам испытаний с уверенностью можно судить о проявлении (или не проявлении) образцом лишь двух видов деформации: мгновенной упругой и высокоэластической. О проявлении мгновенной упругой деформации свидетельствует наличие на кривых ползучести и упругого восстановления равных между собой прямых участков OС и AВ (рис. 10), о проявлении высокоэластической деформации – уменьшение деформации во времени при упругом восстановлении образца.

Для того чтобы выяснить, проявил ли полимер при испытаниях пластическую деформацию необходимо добиться его полной релаксации. Если после полной релаксации кривая упругого восстановления вышла на прямую, параллельную оси абсцисс, то это свидетельствует о том, что образец проявил пластическую деформацию. Если же кривая упругого восстановления совпала с осью абсцисс, значит образец не проявил при испытаниях пластическую деформацию. Таким образом, наблюдение за поведением полимера после снятия нагрузки позволяет разделить высокоэластическую и пластическую деформации. Сделать это по первой части испытаний полимера (изучение ползучести) не представляется возможным, так как под нагрузкой высокоэластическая и пластическая деформации развиваются одновременно.

Величину каждого из проявленных видов деформации также можно определить лишь после полной релаксации полимера. Пусть кривая испытаний полимера, полностью отрелаксировавшего после снятия нагрузки, имеет следующий вид, (рис. 11):

Рис. 11. Кривая испытаний полимера, полностью

отрелаксировавшего после снятия нагрузки

О – момент приложения нагрузки;

А – момент снятия нагрузки.

Первой обычно определяют величину мгновенной упругой деформации. OС – это мгновенная упругая деформация, проявленная образцом под напряжением, AВ – та же деформация, но проявленная им после снятия напряжения. Так как OС = AВ, то величина мгновенной упругой деформации – это величина на оси ординат отрезка OС или равного ему отрезка A´В´.

Следующей определяют величину пластической деформации. Так как в результате отдыха полимера его релаксация прошла полностью, т.е. восстановились и мгновенная упругая, и высокоэластическая деформации, то величина пластической деформации – это величина на оси ординат отрезка OD´, равного по значению величине отрезка ЕD.

Последней определяют величину высокоэластической деформации. Как известно, общая деформация полимера представляет собой сумму мгновенной упругой, высокоэластической и пластической деформаций, откуда:

ε_вэ = ε_общ. - ε_му - ε_пл.

Это значит, что для определения величины высокоэластической деформации можно либо произвести вычисление по данной формуле, либо на оси ординат определить величину отрезка В´D´.