8.4. Мультиплексоры

Мультиплексором (коммутатором) называется устройство, имеющее n адресных входов, 2ⁿ входов данных (информационных), один выход и выполняющее передачу данных (переключение, коммутацию) с одного из информационных входов на выход, в зависимости от двоичного кода, поданного на адресные входы. Мультиплексоры могут иметь управляющий или стробирующий вход. Количество информационных входов может быть равно 4, 8, 16 и тогда мультиплексоры называют 4 на один, 8 на один или 16 на один соответственно. Таблицы истинности и обозначение мультиплексоров приведены на рис. 8.13.

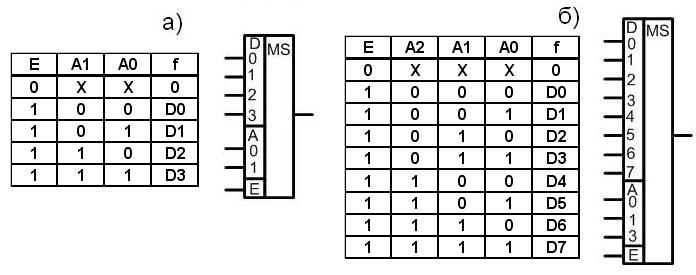
Рис. 8.13. Таблицы истинности и обозначение управляемых мультиплексоров:

а – мультиплексор 4 на 1; б – мультиплексор 8 на 1

В таблице истинности мультиплексоров при Е=0 выходной сигнал всегда равен нулю, поэтому значения переменных А0 и А1 безразличны (обозначены Х).

В мультиплексорах имеется поле адреса (А), на которое подается двоичный код. В соответствии с эти кодом один из информационных входов поля D переключается на выход. Таким образом, функцию выхода мультиплексора 4 на 1 можно записать в следующем виде:

Переменная Е – дополнительная переменная, которая подается на стробирующий вход мультиплексора. При Е=1 и комбинации в поле адреса А=00 на выход переключается информационный вход D₀, при А=01 – вход D₁, при А=10 – вход D₂, при А=11 – вход D₃.

Из анализа формулы 8.2 следует, что функция f мультиплексора содержит логическую сумму функций выходов дешифратора (формула 8.1), причем конъюнкция каждого выхода дополнительно умножается на Е и на значение D_k соответствующего информационного входа (k=0,1,2,3).

Таким образом, мультиплексор состоит из дешифратора для выбора информационного входа и набора элементов И для реализации подключения выбранного информационного входа на выход. Для мультиплексора 4 на 1 схема представлена на рис. 8.14. Для мультиплексоров 8 на один БФ выхода имеет вид:

При комбинации на адресных входах А=000 на выход переключается информационный вход D₀, при А=001 – вход D₁, при А=110 – вход D₆, при А=111 – вход 7 и т. д. В мультиплексор 8 на 1 входит трехразрядный дешифратор, 8 схем И, схема ИЛИ на 8 входов.

Рис. 8.14. Схема мультиплексора четыре на один

8.5. Демультиплексоры

Демультиплексор, это устройство обратное мультиплексору, т. е. входной сигнал коммутируется на одно из нескольких направлений в зависимости от кода на адресных входах. По аналогии с мультиплексорами демультиплексоры можно называть один на четыре, один на восемь и т. д. Таблица истинности демультиплексора 4 на 1, БФ его выходов и схема приведены на рис. 8.15.

Рис. 8.15. Демультиплексор 1 на 4:

а – таблица истинности; б – БФ выходов; в – схема демультиплексора

8.6. Сумматоры

Сумматор – это устройство для арифметического сложения двоичных кодов чисел. Сложение чисел производится поразрядно. Структурная схема четырехразрядного сумматора представлена на рис. 8.16. Здесь, А и В представляют собой четырехразрядные числа. При сложении чисел между разрядами производится перенос.

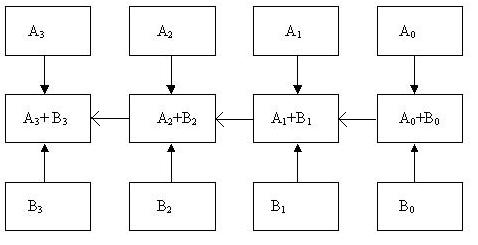
Рис. 8.16. Сумматор для сложения 4-х разрядных двоичных чисел.

Арифметическое сложение подчиняется следующим правилам (рис. 8.17).

Ai	Bi	(A+B)i
0	0	0
0	1	1
1	0	1
1	1	(1)0

Рис. 8.17. Правила и примеры сложения двоичных чисел

Если одноименные разряды обоих чисел равны 1, то значение их суммы равно 0, и возникает перенос, который прибавляется к сумме старших разрядов. В примерах на рис. 8.18 разряды, из которых произошел перенос, выделены.

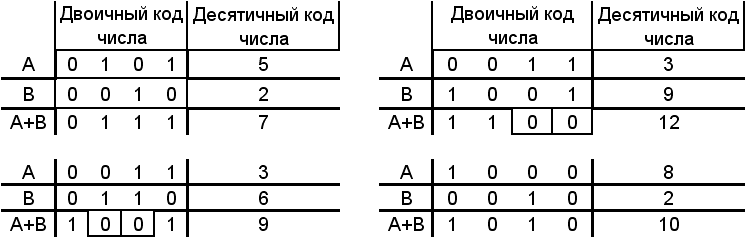
Рис. 8.18. Примеры сложения двоичных чисел

Таким образом, устройство для сложения многоразрядных чисел состоит из ячеек двух типов:

• для сложения самых младших разрядов ячейка должна иметь два входа для приема A₀ и B₀ и два выхода для формирования значения суммы разрядов и переноса в старший разряд;

• для сложения остальных разрядов каждая k-ая ячейка должна иметь три входа для переменных A_k, B_k, переноса из предыдущего разряда P_k-1 и два выхода.

Таблица истинности для нулевого разряда сумматора и карты Карно функций S0 и P0 приведены на рис. 8.19.

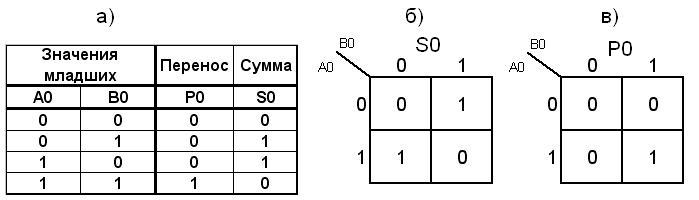
Рис. 8.19. Сумматор младших разрядов:

а – таблица истинности; б – карта Карно функции суммы;

в – карта Карно функции переноса

Из карт Карно следует:

Устройство, описываемое этими функциями, называется полусумматором. Схема полусумматора и его обозначение на схемах показано на рис. 8.20.

Рис. 8.20. Полусумматор:

а – схема полусумматора; б – обозначение на схемах

Для полного сумматора таблица истинности, карты Карно приведены на рис. 8.21. Схема полного сумматора приведена на рис. 8.22. Полный сумматор может быть собран из двух полусумматоров (рис. 8.23, а), обозначение полного сумматора приведено на рис. 8.23 (б).

Рис. 8.21. Полный сумматор:

а – таблица истинности; б – карты Карно для суммы и переноса

Рис. 8.22. Схема полного сумматора

Рис. 8.23. Полный сумматор

а – из двух полусумматоров; б – обозначение полного сумматора

Для сложения n-разрядных чисел нужно использовать один полусумматор для нулевого разряда и n-1 полных сумматоров для остальных разрядов. На рис. 8.24 приведена схема 4-х разрядного сумматора.

Рис. 8.24. Схема сумматора для сложения двух четырехразрядных чисел

123