Лабы / Лабораторные работы по ФХОТЭС. ЮЗГУ / laby-fhotes / КС-61 / lab#6

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ РФ

КУРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА КОНСТРУИРОВАНИЯ И ТЕХНОЛОГИИ ЭЛЕКТРОННЫХ

ВЫЧИСЛИТЕЛЬНЫХ СРЕДСТВ

РАСЧЕТ ОСНОВНЫХ ПАРАМЕТРОВ НИЗКОТЕМПЕРАТУРНОЙ ПЛАЗМЫ

Выполнил студент гр. КС-61

Смирнов А.В.

Проверил Умрихин В.В.

Курск 2008

ЦЕЛЬ РАБОТЫ: Изучить методику расчета параметров низкотемпературной плаз­мы, приме­няемой в технологии электронной аппаратуры (ЭА).

ТЕОРЕТИЧЕКАЯ ЧАСТЬ

Понятие плазмы и ее температура

Плазмой называют ионизованный квазинейтральный газ, занимаю­щий на­столько большой объем, что в нем незаметны нарушения квази­нейтральности из-за тепловых флуктуаций концентрации заряженных частиц.

Квазинеитральностью называют равенство объемных плотностей положи­тельного и отрицательного зарядов. Носителями наряда в плазму служат почти исключительно электроны и положительные ионы. Отношение концентрации ионов к общей концентрации тяжелых частиц называют степенью ионизации газа

, (2.1)

где - концентрация положительных ионов.

Если степень ионизации много меньше единицы, вероятность многократ­ной (двукратной) ионизации токе мала, поэтому носителями положительного заряда оказываются в основном однозарядные ионы и условие квазинейтраль­ности сводится к примерному равенству кон­центраций электронов и поло­жительных ионов :

(2.2)

В этом случае степень ионизации с достаточной точностью мож­но вычис­лять как отношение концентрации электронов к концентрации нейтральных атомов .

Если известно давление Р и температура Т в рабочем объеме (обычно Т - комнатная температура), можно определить концентрацию из следующего выражения:

, (2.3)

где k - постоянная Больцмана.

В различных технологических процессах ионно-плазменной обра­ботки обычно применяется так называемая газоразрядная плазма. Та­кая плазма под­держивается за счет внешнего электрического поля. Ионизация в ней осущест­вляется путем соударения электронов с ней­тральными атомами или молеку­лами. Заряженные частицы (электроны и ионы) ускоряются полем и отдают энергию нейтральным частицам при соударениях, в основном упругих. Энергия выделяется в такой плазме в виде джоулева тепла.

При упругих столкновениях частицы близких масс интенсивно обменива­ются энергией. Массы ионов и нейтральных атомов примерно равны между со­бой, но много больше массы электрона. Поэтому рав­новесное (максвелловское) распределение скоростей гораздо быстрее устанавливается внутри каждого класса частиц, чем между этими классами, и средняя кинетическая энергия электронов оказывается много больше, чем у ионов, а эта последняя - больше средней кине­тической энергии нейтральных атомов. Нужно еще учесть, что сред­няя длина свободного пробега электронов больше таковой для ионов, по­этому внешнее поле интенсивнее “снабжает” их энергией. Все это приводит к тому, что в газоразрядной плазме сосуществуют три ком­поненты с различными температурами: электроны - , ионы - и нейтральные частицу - . при этом

. (2.4)

В этом смысле газоразрядная плазма термически неравновесна (неи­зотер­мическая плазма). Низкотемпературной принято считать плазму с _К.

В резком отличии свойств плазмы от свойств нейтральных газов опреде­ляющую роль играют два фактора. Во-первых, взаимодействие частиц плазмы между собой характеризуется кулоновскими силами притяжения и отталкива­ния, убывающими с расстоянием гораздо мед­леннее (т.е. значительно более “дальнодействующими”), чем силы взаимодействия нейтральных частиц. По этой причине взаимодействие частиц в плазме является, строго говоря, не “парным”, а “коллек­тивным” - одновременно взаимодействует друг с другом большое чис­ло частиц. Во-вторых, электрические и магнитные поля очень сильно действуют на плазму, вызывая появление в плазме объемных зарядов и токов и обусловливая целый ряд специфических свойств плазмы. Эти отличия позволяют рассматривать плазму как особое четвертое состояние вещества.

Дебаевский радиус экранирования и идеальность плазмы

Важным параметром, характеризующим свойства плазмы является, деба­евский радиус экранирования, определяющий расстояние, на ко­тором в плазме распространяется действие электрического поля отдельного заряда. В вакууме электростатический потенциал уединенной частицы с зарядом е на расстоя­нии r определяется по формуле

(2.5)

В среде, содержащей положительные и отрицательные заряды, напри­мер в плазме, электроны в некоторой окрестности положительного иона притягива­ются к нему и экранируют его электростатическое по­ле. Точно так же “неподвижный” электрон отталкивает другие элект­роны и притягивает поло­жительные ионы. В результате поле вокруг заряженной частицу становится очень слабым на расстояниях, превы­шающих дебаевский радиус экранирова­ния. Выражение для потенциала заряда, покоящегося в плазме, принимает вид

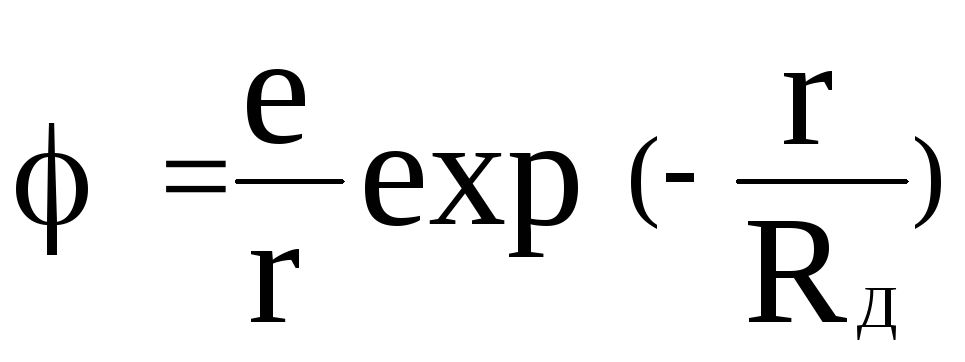. (2.6)

где - дебаевский радиус экранирования, зависящий от концентрации заря­женных частиц, энергии их теплового движения (температуры) и величины за­ряда. Для неизотермической плазмы ()

(2.7)

При подстановке значений констант получим

, (2.8)

где - электронная температура в К.

Из формулы (2.6) видно, что кулоновское поде заряда начинает сущест­венно искажаться на расстояниях от него, а вдали, при ^, поле быстро спадает по экспоненциальному закону. Это яв­ляется результатом гаше­ния поля центральной частицы противоположно направленным полем про­странственного заряда.

Плазма считается идеальной, если потенциальная энергия взаи­модействия частиц мала по сравнению с их тепловой энергией. Это условие выполняется, когда число частиц в сфере радиуса велико:

(2.9)

Плазменная частота

Допустим, что в начальный момент под действием какой-то внешней силы все электроны в плазме оказались сдвинутыми относи­тельно ионов. Вследствие разделения зарядов немедленно возникает кулоновская сила их притяжения, которая стремится вернуть заряды “на место”, но, будучи ускоренными этой силой, электроны “проска­кивают” положение равновесия и смешатся относи­тельно ионов вле­во, и т.д. Возникают собственные колебания электронного газа как целого относительно ионов, которые с большой степенью точности можно считать неподвижными.

Частоту колебаний легко вычислить с помощью схемы (рис. 2.1). Если - смещение электронов из положения равновесия, то плотность поверхно­стного заряда на границах слоя равна .

Рис. 2.1. Схема, поясняющая возникнове­ние плазменных колебаний и вывод фор­мулы для плазменной частоты.

Возвращающая сила пропорциональна смещению, следовательно, уравне­ние дви­жения электрона

(2.10)

(2.11)

описывает гармонические колебания с частотой , определяемой по формуле

. (2.12)

Проводимость плазмы

Под действием электрического поля в плазме возникает элек­трический ток. Ток через плазму обеспечивается главным образом движением электронов, так как они гораздо более подвижны, чем ио­ны. Правда, различие в подвиж­ности не столь велико, как отношение масс , ибо частота столкновений ионов существенно меньше таковой для электронов из-за малой скорости ио­нов. Подвижность ио­нов обычно в сотни раз меньше, чем у электронов, и по­этому вклад ионов в электрический ток пренебрежимо мал, за исключением тех нечастых случаев, когда плотность положительных или отрицательных ионов сильно превышает электронную .

Плотность электрического тока в пренебрежении ионным током есть

, (2.13)

где - дрейфовая скорость электронов; - подвижность электро­нов; - проводимость.

Проводимость плазмы пропорциональна плотности и подвижности электронов и принимает вид

, (2.14)

где - эффективная частота столкновений электрона.

Подвижностью называется коэффициент пропорциональности между вели­чинами скорости и дрейфа заряженной частицы и поля. Подвиж­ность электро­нов выражается следующей формулой:

, (2.15)

. (2.16)

В несильных электрических полях скорость дрейфа ионов значи­тельно меньше скорости хаотичного движения , a сама хаоти­ческая скорость определяется просто температурой газа, так как ионы интенсивно обменива­ются с молекулами кинетической энергией, и приходят в тепловое равновесие с газом. При небольших энергиях подвижность не зависит от поля и равна

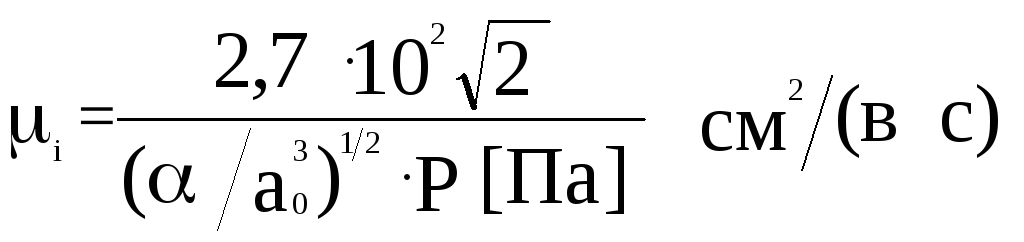, (2.17)

где - коэффициент поляризуемости атомов и молекул, - боровский радиус . Для газов значения соотношения равны: Не – 1,39; Ne – 2,76; Ar – 11,1; -5,52; - 11,8.

При степени ионизации 0,1% проводимость становится практически неза­висящей от плотностей газа и электронов, определяясь только электронной температурой. В этом случае проводимость определяется следующим выраже­нием:

(2.18)

Диффузионные процессы в плазме

Расплывание облака ионизированного газа в отсутствие поля или в на­правлении, поперечном полю, обязано диффузии заряженных частиц. Коэффи­циенты диффузии электронов и ионов сильно различа­ются по величине из-за того, что легкие электроны движутся гораз­до быстрее, чем ионы. В принципе, спустя некоторое время, электроны могли бы оставить далеко позади своих ме­нее подвижных партне­ров. На месте первоначального облака и его окрестностях на более длительное время остался бы нескомпенсированный по­ложительный за­ряд, Так и происходит на самом деле, но только в тех случаях. Когда плотности зарядов невелики. Лишь при низкой плотности отри­цательно и положительно заряженные частицы диффундируют независи­мо. Это явление называется свободной диффузией.

Если плотности частиц обоих знаков не малы, в результате их разделения образуется значительный пространственный заряд, а воз­никшее электрическое поле поляризации препятствует дальнейшему нарушению электронейтрально­сти. Отрицательные и положительные за­ряды как бы не могут при этом оторваться друг от друга, будучи связанными электрическими кулоновскими силами. Разделение зарядов и поле поляризации автоматически так подстраи­ваются друг к другу, чтобы поле сдерживало убегающие электроны, подтяги­вало к ним тяжелые ионы и заставляло их диффундировать только “вместе”. Такая диффузия называется амбиполярной. Это понятие было введено Шоттки в 1924 году.

В случае свободной диффузии для частиц выполняется соотношение Эйн­штейна

(2.19)

где D - коэффициент свободной диффузии. Т - температура.

Для диффузионного потока заряженных частиц того и другого знака коэф­фициент амбиполярной диффузии записывается в следующем виде:

(2.20)

где , - подвижности электронов и ионов, соответственно; , - коэф­фициенты свободной диффузии электронов и ионов.

В неравновесной плазме, где “температура” электронов сущест­венно выше ионной, которая совпадает с температурой газа:

. (2.21)

Диффузия становится амбиполярной, если размеры объема, в ко­тором на­ходится плазма значительно больше дебаевского радиуса эк­ранирования , где - размер объема. При электроны и ионы диффун­дируют независимо.

Следует отметить, что диффузия к стенкам, и свободная, и амбиполярная, являются одним из действенных механизмов гибели заря­дов. Как правило, стенки играют каталитическую рель, способствуя нейтрализации зарядов.

Влияние магнитного поля

В некоторых технологических процессах наряду с электрическим полем присутствует магнитное поле (например, метод магнетронного распыления ма­териалов).

Пусть на ионизированный газ наложено постоянное однородное магнитное поле Н. Если поля Е и Н параллельны, то никакого влия­ния на дрейф заряжен­ных частиц магнитное поле не оказывает.

. (2.22)

В случае произвольно направленного магнитного поля вектор

всегда можно представить в виде суммы параллельной и перпендику­лярной Е составляющих, достаточно рассмотреть случай скрещенных полей, когда .

Рис 2.2. Дрейф в скрещенных полях Е и Н.

Спроектируем уравнение (2.23) на координатные оси:

(2.24)

Составляющие скорости дрейфа равны:

(2.25)

где - обычная подвижность в отсутствие магнитного поля, а

, (2.26)

- так называемая гиромагнитная циклотронная частота. С такой частотой электрон вращается в пустоте вокруг магнитного вектора, если у него есть пер­пендикулярная этому вектору составляющая ско­рости.

Итак, в скрещенных полях скорость дрейфа имеет иное направление, чем электрическое поле, т.е. подвижность является тенгором. Подвижность электронов в направлении электрического поля меньше обычной. Возникает дрейф в направлении, перпендикулярном обоим полям. В направлении магнит­ного поля дрейфового движения нет. Поперечная обоим полям скорость появляется под действием лоренцевой силы. Скорость вдоль Е уменьша­ется из-за того, что лоренцева сила все время стремится отклонить дрейфую­щий вдоль Е электрон в сторону. Тем самым создается дополнительная к столкновениям помеха ускорению заряда электрическим полем.

ХОД РАБОТЫ

Вариант №12

Исходные данные:

1. Найти электронную плотность .

2. Определить дебаевский радиус экранирования .

Рис.1. График зависимости между электростатическим потенциалом и расстоянием, на которое в плазме распространяется действие электрического поля отдельного заряда

3. Установить идеальность плазмы .

4. Найти плазменную частоту .

5. Найти подвижности ионов и электронов.

6. Определить проводимость плазмы .

7. Найти коэффициенты свободной диффузии для ионов и электронов.

8. Найти коэффициент амбиполярной диффузии .

9. Найти циклотронную частоту вращения электрона .

ВЫВОД: в ходе лабораторной работы я изучил методику расчета параметров низкотемпературной плаз­мы, приме­няемой в технологии электронной аппаратуры (ЭА).