3.2. Механизмы образования на поверхности кремния диэлектрических пленок

3.2.1. Этапы роста окисной пленки

Изучение кинетики возникновения и роста окисных пленок ме­таллов и полупроводников имеет важное значение для решения ряда задач микроэлектроники, в первую очередь для создания рациональ­ной технологии изготовления микроэлектронных активных и пассивных элементов. Диэлектрические пленки в микросхемах выполняют различ­ные функции. Они широко применяются в качестве подзатворных диэ­лектриков, межслойной и межкомпонентной изоляции, пассивирующих слоев. Высокие изолирующие и стабилизирующие качества слоев двуо­киси кремния определили широкое применение в полупроводниковой технологии.

Различают два этапа роста окисной пленки: начальный этап при низкой температуре и диффузионнный этап (высокотемпературное окисление). Начальный этап образования пленки связан с процессом перехода электронов от поверхностных атомов кристалла к адсорби­рованным на этой поверхности атомам кислорода. Со стороны крис­талла возникает слой положительных ионов (слой, обедненный элект­ронами), а со стороны газа - слой отрицательных ионов. В этом двойном слое появляется сильное электрическое поле, которое вызы­вает направленное к внешней поверхности пленки движения положи­тельно заряженных атомов основного вещества (катионов). Катионы на поверхности пленки связываются с отрицательно заряженными ато­мами кислорода (анионами) и достраивают следующий слой пленки. На пленке вновь адсорбируются атомы кислорода, к которым из металла благодаря туннельному эффекту поступают электроны. Стадия форми­рования окисной пленки прекращается при достижении толщины пленки порядка десятка атомных слоев, что вызвано резким спадом вероят­ности туннельного эффекта.

В отличие от первого этапа второй этап окисления полностью определяется процессами диффузии. При высокой температуре проис­ходит процесс диффузионного перемещения либо окисляемого вещества и электронов к поверхности раздела “окисел-газ”, либо атомов кисло­рода в объем основного вещества. Соответственно реакция окисления протекает либо на границе раздела “окисел-газ”, либо на границе раздела “окисел - окисляемое вещество”. В каждом конкретном случае проявляется тот или иной процесс диффузионного перемещения либо их сочетание.

3.2.2. Механизм термического окисления кремния

В настоящее время не существует законченной теории термичес­кого окисления полупроводников. Исторически сложилось так, что первые кинетические модели в этой области основывались на сущест­вовавших моделях окисления металлов.

Одной из первых кинетических моделей, успешно примененных для описания процесса окисления кремниевых пластин в температур­ном диапазоне 973-1573 К, при давлениях окислителя (0,2-1,0)10⁸ Па и толщине окисных пленок >50 нм, явилась модель Дила-Гроува. Она широко использовалась а теории и практике формирования пленок диоксида кремния, но при переходе к более тонким слоям SiO₂ стал особенно очевидным ее ограниченный характер

Следует иметь в виду, что перед началом высокотемпературного окисления на поверхности кремния уже имеется слой окисла некото­рой малой, но конечной толщины d_ок, возникший в результате низко­температурного окисления.

Процесс окисления кремния в установившемся режиме слагается из следующих этапов. Молекулы окислителя (молекулы кислорода или пары воды) адсорбируются на поверхности двуокиси кремния, созда­вая концентрацию N₁. Величина концентрации адсорбированных частиц окислителя прямо пропорциональна давлению газа при условии от­сутствия диссоциации или ассоциации окислителя на поверхности. Это условие обычно выполняется при окислении кремния. Далее час­тицы окислителя диффундируют сквозь окисный слой к границе SiO₂ - Si. На границе раздела сред "окисный слой - кремний" атомы кисло­рода вступают в реакцию с атомами кремния, в результате чего уве­личивается толщина окисного слоя. При этом в процессе установив­шегося окисления предполагается, что в слое двуокиси кремния и на границах раздела сред отсутствует накопление атомов окислителя. Очевидно, что поток окислителя из одной среды в другую возникнет только в том случае, если существует разность концентраций на границах фаз. Пусть в слое окисла на границе с окружающей средой концентрация молекул окислителя равна N₂, а на границе раздела SiO₂ - Si со стороны двуокиси кремния составляет N₃ (см. рис.3.6).

Рис. 3.6. Распределение концентрации кислорода в установившемся процессе окисления

Следует иметь в виду, что в величины указанных концентраций окислителя в окисном слое N₂ и N₃ не входит концентрация кислоро­да, вступившего в реакцию с кремнием и образовавшего химическое соединение Si₂O.

Модель Дила-Гроува исходит из наличия в системе кремний-ди­оксид кремния-газ трех кислородосодержащих потоков (рис.3.1): J₁, J₂, J₃.

Первый из них связан с переносом кислородосодержащих частиц в газовой среде, второй - через окисную пленку, третий - непос­редственно в реакционную зону. Поток частиц окислителя от газовой среды в слой двуокиси кремния равен

J₁ = h(N₁ - N₂), (3.34)

где h - коэффициент массопереноса кислорода через поверхность.

Внутри слоя окисла окислитель будет диффундировать к границе SiO₂ - Si. Учитывая, что процесс окисления является установившимся и накопления частиц окислителя в слое окисла нет, поток окислителя в любой точке слоя окисла одинаков и равен

, (3.35)

где x - толщина слоя в любой момент времени, а D - эффективный коэффициент диффузии. Следует уточнить, что диффузия в слое двуо­киси кремния происходит под действием двух причин: вследствие градиента концентрации частиц, а также вследствие дрейфа в элект­рическом поле, созданном объемным зарядом. Объемный заряд в свою очередь создан окислителем, который диффундирует в окисле в виде молекулярных ионов. Если толщина слоя окисла больше толщины слоя объемного заряда, то эффективный коэффициент диффузии примерно в два раза больше, чем истинный коэффициент диффузии. Поток диффу­занта, вступающего в реакцию с кремнием, пропорционален концент­рации окислителя в слое окисла на границе раздела с кремнием:

J₃ = kN₃, (3.36)

где к - константа скорости реакции окисления.

В условиях равновесия все рассмотренные потоки равны, т.е

J₁ = J₂ = J₃ = J. (3.37)

Подставляя полученные выражения для потоков в (3.37), найдем формулы для концентраций N₂ и N₃:

(3.38)

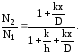(3.39)

Если в уравнение (3.36) подставить выражение для N₃ из (3.38), то получим формулу для потока частиц в установившемся процессе окисления:

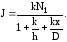(3.40)

Пусть на образование единицы объема слоя двуокиси кремния идет N молекул окислителя, тогда поток J будет выражаться уравне­нием

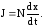(3.41)

Подставляя в формулу (3.41) выражение для потока J найдем скорость роста окисного слоя

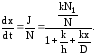(3.42)

С помощью полученного уравнения можно найти зависимость тол­щины окисла от длительности процесса. Начальным условием для ре­шения этой задачи является

х = х₀ при t = 0. (3.43)

Для упрощения записей введем следующие обозначения:

(3.44)

(3.45)

Интегрирование уравнения (3.42) дает

(3.46)

где t₀ – смещение по оси времени, равное предполагаемой длительности роста начального слоя окисла х₀ в условиях рассматриваемого процесса:

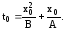(3.47)

Решение уравнения (3.46) для x как функция времени записыва­ется в виде:

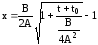. (3.48)

Рассмотрим предельные случаи:

1) при больших временах окисления, когда t>>B/(4A²), в этом случае

х² = Bt; (3.49)

уравнение (3.49) представляет собой параболический закон роста диоксида кремния, а B - параболическую константу скорости окисления;

2) другой предельный случай имеет место при малых временах окисления, когда справедливо соотношение (t + t)<< B/(4A²) и ограни­чиваясь первым членом разложения в ряд Тэйлора уравнения (3.48), получим

x = A ( t + t₀). (3.50)

Таким образом, в начале процесса окисления рост пленки окисла описывается линейным законом, а скорость роста в этом случае, как видно из выражения (3.44), ограничивается скоростью переноса окислителя через поверхность в слой двуокиси кремния h и скоростью реакции окисления k на границе SiO₂-Si. Экспериментальные исследования показывают, что величина h на несколько порядков больше величины k для реальных условий окисления. Следовательно, выражение (3.44) может быть переписано в виде Ak(N₁/N).

В промежуточном случае наблюдается постепенный переход от ли­нейного закона к параболическому (рис.3.6).

Рис.3.6. Зависимость толщины слоя окисла от длительности процесса окисления: штриховыми линиями показаны параболическая и линейная зависимости

Характер линейной зависимости константы диффузии реагента В от давления паров подтверждают экспериментальные данные. В противном случае окислитель диссоциировал на поверхности. Если бы такая диссоциация на поверхности образца наблюдалась, то зависимость В от давления носила бы квадратичный характер.

Константа диффузии реагента В или соответственно параболического роста пленки окисла пропорциональна также коэффициенту диффузии D и, следовательно, должна зависеть от температуры.

Константа скорости химической реакции А на границе SiO₂-Si (константа линейного роста) также зависит от температуры. Учитывая, что величины N и N₁ практически не зависят от температуры, температурная зависимость константы А обусловлена зависимостью скорости реакции окисления k на границе SiO₂-Si от температуры. Скорость реакции окисления определяется энергией, которую необходимо затратить для разрыва ковалентной связи атомов решетки Si-Si.