Решая (3.8) относительно d, находим

D = ns²/(6t). (3.9)

В выражении (3.9) величина n/t представляет собой число эле­ментарных скачков частицы в единицу времени. Выразим ее через об­ратную величину:

t/n = , (3.10)

где - время между очередными скачками частицы (время ее оседлой жизни).

Подставив (3.10) в (3.9), найдем

D = s²/(6). (3.11)

Как видно из (3.11), коэффициент D представляет собой отно­шение квадрата длины элементарного скачка к времени оседлой жизни частицы, отнесенное к одному из шести возможных направлений ее хаотического блуждания. Если длину элементарного скачка частицы выразить в сантиметрах, а среднее время ее оседлой жизни - в се­кундах, то этот коэффициент приобретает размерность см²/с. Таким образом он показывает, как быстро со временем смещаются хаотичес­ки блуждающие частицы. Тем самым он служит фундаментальной харак­теристикой элементарного акта хаотической самодиффузии как собы­тия, отображающего динамику разупорядочения кристалла, связывая это событие со временем.

В разных по своей природе кристаллах вероятность таких собы­тий, конечно, различна. Таким образом, коэффициент хаотической самодиффузии можно определить как величину, характеризующую спо­собность атомов данного вещества к взаимному перемешиванию.

Среднее время нахождения атома в одном из положений равнове­сия

t = 1/W = t₀ exp[E/(k T)]. (3.12)

Здесь t₀ - постоянная, соизмеримая с периодом собственных колеба­ний атомов в узлах решетки (~ 10^-13 с).

С учетом (3.12) выражение для коэффициента диффузии может быть представлено в виде

D = Do exp[-E/(kT)], (3.13)

где D₀ = k₀s2/t₀; k₀ - коэффициент, зависящий от структуры крис­талла и механизма диффузии. Для объемно-центрированной кубической решетки при диффузии по вакансиям k₀ = 1/8, a при диффузии по междоузлиям k₀ = 1/24.

Выражение (3.13) справедливо для процессов самодиффузии и диффузии примесных атомов как по вакансиям, так и по междоузлиям кристаллической решетки и было получено шведским ученым Свенте Аррениусом. Поэтому его часто называют уравнением Аррениуса.

Механизмы диффузии различных элементов определяются главным образом типом твердого раствора, который они образуют в кристал­лической решетке, т.е. тем, располагаются ли примесные атомы в узлах или междоузлиях кристаллической решетки (твердые растворы замещения или внедрения соответственно) или образуют растворы смешанного типа (атомы размещаются по узлам и междоузлиям).

При диффузии примесных атомов по вакансиям одновременно про­текает процесс самодиффузии. Однако этот процесс идет значительно медленнее, так как химическая связь между атомами вещества силь­нее связи примесных атомов с решеткой.

Механизмы диффузии примесных атомов в кристаллической решет­ке при изменении температуры и концентрации примеси может изме­няться. В промежуточной переходной области возможна диффузия по обеим механизмам. При изменении механизма диффузии изменяются и параметры k₀, D₀, E, D.

Существенное влияние на скорость диффузии оказывают атомы примеси и другие дефекты, присутствующие в кристалле. Локальная деформация решетки вблизи примесного атома приводит к уменьшению энергии связи между соседними атомами, что увеличивает вероят­ность образования вакансий. При вакансионном механизме диффузии это приводит к увеличению скорости диффузии. Энергия активации процесса диффузии может изменяться также вследствие кулоновского взаимодействия между атомами диффузанта и присутствующей в решет­ке примеси. Так, в германии и кремнии наличие акцепторной примеси ускоряет, а наличие донорной примеси замедляет процесс диффузии атомов донора.

Скорость диффузии примесей в полупроводниках обратно пропор­циональна их предельной растворимости. Высокая растворимость при­месей наблюдается в случае образования твердых растворов замеще­ния. В случае когда атомы примесей в силу их слабой связи с ре­шеткой не могут замещать узлы, образуются твердые растворы внед­рения, область растворимости сужается, так как в междоузельном пространстве может разместиться меньшее количество атомов. Ско­рость же диффузии примесей по междоузлиям значительно выше ско­рости диффузии по вакансиям решетки.

Однако во многих случаях введение инородных атомов приводит к возникновению в диффузионной области новой фазы (химического соединения) с другой структурой и другими физическими свойствами, чем основное вещество. Такой процесс получил название “реактивная диффузия”. Возникновение новой фазы приводит к замедлению процесса диффузии по следующим причинам. Поскольку диффундирующие атомы связываются с атомами основного вещества, то происходит постепенное уменьшение диффузионного потока. Кроме того, с ростом толщины слоя новой фазы увеличивается путь, по которому должны проходить диффундирующие атомы, чтобы проникнуть в объем основного вещества.

3.1.2. Физико-математические основы процессов диффузии

Законы фика. При диффузии в изотропной среде, обусловленной только градиентом концентрации и при условии независимости коэффициента диффузии от концентрации, выражение для потока диффундирующего вещества (при­меси) имеет следующий вид:

J = - D grad N, (3.14)

где J - вектор плотности потока диффундирующего вещества, т.е. количество вещества, проходящего за единицу времени через единичную площадь поверхности, перпендикулярной направлению перемещения вещества; D - ко­эффициент диффузии; N - концентрация атомов диффундирующего ве­щества.

Знак минус в выражении (3.14) указывает, что диффузионный перенос вещества происходит в направлении уменьшения концентрации примеси.

Когда концентрация вещества изменяется лишь в направлении оси Х, поток

J(x) = - D (dN/Dx). (3.15)

Здесь dN/dx - градиент концентрации диффундирующего вещества. Выражение для скорости накопления диффундирующего вещества может быть получено из (3.15) и принципа сохранения, согласно ко­торому изменение концентрации вещества в определенном объеме должно быть равно соответствующему потоку его в данный объем:

dN/dt = - dJ/dx . (3.16)

При подстановке (3.15) в (3.16) получаем для одномерного случая

(3.17)

Когда коэффициент диффузии можно считать постоянным, выра­жение (3.17) может быть записано как

. (3.18)

Выражения (3.14) - (3.18) впервые были получены в 1885 г. швейцарским ученым Фиком для описания диффузионных процессов в идеальных газах и растворах. В дальнейшем была показана примени­мость установленных законов для описания процессов диффузии в твердых телах. Уравнения (3.14) и (3.18) носят названия первого и второго законов Фика соответственно.

На основании этих законов при заданных начальных и граничных условиях, а также при известном коэффициенте диффузии могут быть решены задачи нахождения: распределения примеси; потока вещества через заданную поверхность, количества продиффундировавшего ве­щества и др.

Решение уравнения диффузии (3.18) для неограниченного тела при заданном в общем виде начальном распределении примесей

N(x,0) = f(x) (3.19)

находят методом разделения переменных. Если концентрацию N(x,t) представить как произведение двух функций, каждая из которых за­висит только от одной переменной N(x,t) = T(t)X(x), то выражение (3.18) принимает вид

(3.20)

или

. (3.21)

Так как левая часть равенства (3.21) не зависит от х, а пра­вая - от t , то они должны быть тождественно равны некоторой пос­тоянной отрицательной величине, которую обозначим -².

В результате получим дифференциальные уравнения

dT/T = - ²Ddt ,

(3.22)

d²X/dx² = - ² X ,

общее решение которых имеют вид

(3.23)

где - текущая координата интегрирования.

Наиболее часто при расчете распределения концентрации приме­си приходится решать уравнения диффузии в тело, ограниченное плоскостью Х = 0.

Диффузия в полуограниченное тело из постоянного источника. Важное практическое значение имеет случай, когда на границе полубесконечного кристалла поддерживается постоянная концентрация диффундирующей примеси. Начальная концентрация во всем полуограниченном теле равна нулю. Граничные условия для этого случая

N(0,t) = N₀. (3.24)

Решение уравнения диффузии для этого случая имеет вид

, (3.25)

где символ erfc означает дополнение (до единицы) функции ошибок

, (3.26)

а erfc z обозначает интеграл функции ошибок Гаусса

. (3.27)

Величину, имеющую размерность длины, называют диффузионной длиной.

Из выражения (3.25) следует, что заданное распределение при­меси можно получить при различных сочетаниях значений D (т.е. температуры) и времени. Кроме того, величина температурно-времен­ного воздействия (Dt) определяет при постоянной концентрации ко­личество примеси, введенное в кристалл, т.е. дозу легирования (рис. 3.3).

Во многих практических случаях важно знать количество диффузанта (дозу легирования), проникшего в тело за время проведения диффузии. Эта величина может быть определена по формуле

, (3.28)

где J(0,t) – поток диффузанта в объем тела через плоскость х=0, равный

. (3.29)

Подставляя (3.25) в (3.29), получим

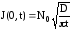. (3.30)

Интегрируя полученное выражение по времени, найдем

. (3.31)

Рис.3.3. Распределение примеси при диффузии из постоянного источника в полуограниченное тело при различных значениях Dt: 1 – Dt=0; 2 – Dt=1; 3 – Dt=4; 4 – Dt=16; 5 – Dt=

Диффузия из слоя конечной толщины в полуограниченное тело. Допустим, что в слое толщиной h, примыкающей к границе полуограниченного тела, имеется равномерно распределенная примесь с концентрацией N₀, а во всей остальной части тела при x>h концентрация примеси равна нулю. Будем считать, что поток примеси через границу х=0 отсутствует. Такие границы принято называть отражающими. Примером отражающей границы может служить поверхность кристалла кремния, покрытого слоем двуокиси кремния. Поскольку коэффициент диффузии большинства диффузантов в двуокиси кремния на несколько порядков меньше, чем в кристалле кремния, то проникновением примеси в слой двуокиси кремния практически можно пренебречь.

Распределение примеси в любой момент времени для этого случая выражается формулой

. (3.32)

Графики этого распределения приведены на рис.3.4. В отличие от предыдущих случаев в данном случае диффузия ведется из ограниченного источника диффузанта. Количество диффузанта, равное Q=N₀h, в процессе диффузии остается неизменным. Происходит лишь перераспределение этого диффузанта по объему тела.

Диффузия из бесконечно тонкого слоя (ограниченный источник) в полуограниченное тело. Если в предыдущем случае устремить толщину слоя h к нулю, то получим распределение примеси при диффузии из бесконечно тонкого слоя в полуограниченное тело с отражающей границей. Если полагать, что с устремлением h0 количество диффузанта Q в слое остается неизменным (за счет соответствующего роста N₀), то распределение примеси запишется так:

. (3.33)

Полученная функция известна под названием “распределение Гаусса”. На рис. 3.5 приведены кривые этого распределения для нескольких значений Dt.

Двухстадийная диффузия. Диффузия из постоянного источника яв­ляется реальным случаем в производстве интегральных схем и предс­тавляет собой первый этап диффузии, задачей которого является введение в кристалл определенного количества примеси. Для умень­шения температурного воздействия (уменьшения фактора Dt) поверх­ностную концентрацию выбирают максимально возможной, т.е. соот­ветствующей предельной растворимости примеси при выбранной темпе­ратуре диффузии. В результате образуется тонкий приповерхностный слой, насыщенный примесью. В производстве этот этап нередко назы­вают загонкой примеси.

Рис.3.4. Распределение примеси при диффузии из слоя конечной толщины h при различных значениях Dt: 1 – Dt=0; 2 – Dt=1/16; 3 – Dt=1/4; 4 – Dt=1; 5 – Dt=4

Рис.3.5. Распределение примеси при диффузии из бесконечно тонкого слоя в полуограниченное тело при различных значениях Dt: 1 – Dt=1/16; 2 – Dt=1/4; 3 – Dt=1

Для окончательного формирования диффузионной области введен­ную на первом этапе примесь подвергают перераспределению. Этот второй этап диффузии, называемый разгонкой примеси, соответствует диффузии из ограниченного источника примеси.

В этом случае примесь диффундирует из поверхностного слоя кремния вглубь, тогда как поступление примеси из окружающей среды отсутствует. При этом поверхностная концентрация N_o с течением времени убывает.

Следует иметь в виду, что последующие операции обработки ИС, связанные с нагревом (диффузия, окисление и т.п.), влекут за со­бой продолжение диффузии примеси. Поэтому в выражение для распре­деления Гаусса вместо Dt должна входить сумма D_it_i, где D_i - ко­эффициент диффузии примеси для температуры, при которой выполня­ется i-я операция; t_i - время выполнения i-ой операции (i=1,2,..n); n - число операций, связанных с последующим нагревом пластины (включая рассматриваемый этап разгонки примеси).