3. Физико-химические основы полупроводниковой технологии

3.1.Закономерности и механизмы диффузии примесей в полупроводниках и планарных твердотельных структурах

3.1.1. Механизмы диффузии атомов в кристаллах

В реальной кристаллической решетке атомы при определенных условиях могут обладать большой свободой передвижения и переме­щаться из одних узлов решетки в другие. Перенос вещества, обус­ловленный хаотическим тепловым движением атомов, в направлении уменьшения их концентрации называется диффузией. Диффузия в крис­талле, находящемся в состоянии химического равновесия (однород­ный химический состав, однородное распределение дефектов), назы­вается самодиффузией. Диффузия атомов в кристалле при наличии градиента химического потенциала (градиента концентрации вещест­ва) носит название гетеродиффузии, химической диффузии или просто диффузии.

Диффузия атомов в кристаллической решетке осуществляется от­дельными скачками из одного положения равновесия в другое. Длина таких элементарных перемещений имеет порядок постоянной решетки, т.е. несколько десятых долей нанометра. За счет таких элементарных скачков атомы могут перемещаться на большие расстояния. Возможны три механизма атомных скачков: взаимный обмен местами, движение по вакансиям и перемещение по междоузлиям. Первый механизм может осуществляться при одновременном обмене местами двух, трех (и бо­лее) соседних атомов. Обмен местами двух соседних атомов является простейшим актом диффузии (рис.3.1,а). Однако при этом в плотно упакованной структуре атом должен преодолеть большой потенциаль­ный барьер, что обусловлено необходимостью смещения соседних ато­мов. При кольцевом обмене (рис.3.1,б) три, четыре или большее число атомов согласовано перемещаются на одно межатомное расстоя­ние. При таком перемещении потенциальный барьер, преодолеваемый каждым атомом, меньше, чем в первом случае. Однако вероятность осуществления такого диффузионного механизма уменьшается с увели­чением числа атомов в кольце за счет возрастания суммарной энер­гии, затрачиваемой на элементарный акт перемещения. Диффузионные процессы, обусловленные механизмом атомных скачков, могут проте­кать в совершенных кристаллических решетках с рыхлой упаковкой.

Диффузия по вакансиям происходит следующим образом: вначале в решетке образуются вакансии, затем они последовательно переме­щаются по кристаллу (рис.3.2,а).

При диффузии атомов по междоузлиям происходят перескок атома из узла решетки в междоузлие и последующие перемещения его уже только по ним (рис.3.2,б).

Рис.3.1. Механизмы диффузии при обмене местами атомов

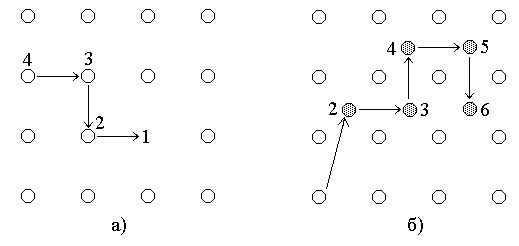
Рис.3.2. Механизм диффузии атомов по вакансиям (а) и междоузлиям (б)

Эти два механизма диффузии наиболее вероятны в реальных кристаллах с большой концентрацией дефектов. Модели механизмов диффузии атомов по вакансиям и междоузлиям были предложены Я.И.Френкелем в 1926 г. В рамках кинетической теории кристаллов, развитой Я.И.Френкелем, эти механизмы можно представить следующим образом. Атомы, находящиеся в узлах кристаллической решетки, на­ходятся в непрерывном тепловом движении около центра равновесия. Часть из них приобретает энергию, достаточную для преодоления по­тенциального барьера, удерживающего их в положении равновесия. Такие атомы переходят из положения равновесия в узле решетки в неравновесное положение в междоузлии. При этом образуется дефект по Френкелю (атом в междоузлии и пустой узел - вакансия).

Наряду с дефектами по Френкелю в кристаллической решетке мо­гут образовываться только вакансии - дефекты по Шоттки. Они воз­никают при выбросе за счет тепловых колебаний одного из поверх­ностных атомов из положения равновесия так, что он сохраняет с кристаллом только частичную связь (адсорбированное состояние).

Вакансии, образующиеся за счет дефектов по Френкелю и по Шоттки, в результате тепловых колебаний могут быть легко замещены соседними атомами, что приводит к их перемещению по узлам крис­таллической решетки. В кристалле при тепловом равновесии содер­жится определенное количество вакансий. Их концентрация увеличи­вается с температурой по экспоненциальному закону

N_v ~ exp(- E_v/(k T), (3.1)

где Е_v - энергия, затрачиваемая на образование вакансии; k = 8.6310^-5 эВ/град - постоянная Больцмана;Т - температура кристалла.

Концентрация равновесных вакансий в кристаллических решетках германия и кремния при комнатной температуре составляет 10¹³ – 10¹⁴ м^-3 и увеличивается с повышением температуры, а также при возрастании концентрации примесей и дефектности решетки. Так, в условиях термодинамического равновесия в кремнии при температурах 1273 – 1473 К N_v = 10²¹ – 10²² м^-3.

При достижении концентрацией значения 510²⁵ м^-3 (т.е. когда количество вакансий приближается к 10^-3 % от количества узлов) кристалл плавится.

Внедренные в междоузлия атомы могут относительно легко пере­мещаться по ним, так как они связаны с решеткой слабее, чем ато­мы, находящиеся в узлах. За счет этого атомы в решетке с дефекта­ми могут обладать достаточно высокой подвижностью. Скорость пере­мещения атомов, выраженная как вероятность их перехода из одного равновесного положения в другое вследствие статистического харак­тера процесса, возрастает с повышением температуры по экспоненци­альному закону

W = Wo exp[- E/(kT)], (3.2)

где Е – потенциальный барьер (энергия активации), преодолеваемый атомом при переходе из одного положения равновесия в другое, вы­сота которого определяется характером химической связи атомов в кристалле и механизмом диффузии.

Хаотическая самодиффузия. Коэффициент хаотической самодиффузии. Качественную характеристику особенностей различных меха­низмов диффузии дополним количественной характеристикой. Это мо­жет быть сделано путем введения специального параметра, называе­мого коэффициентом диффузии.

Силовой рельеф, образуемый полем, связывающим частицы кристалла, имеет такую же периодическую структуру, как и решетка кристалла. Для диффундирующей частицы он представляется в виде периодических потенциальных барьеров определенной высоты, препятствующих ее движению по кристаллу. Преодолеть такой барьер способна лишь частица с необходимым для этого уровнем энергии, случайно приобретенным в результате тепловой флуктуации. Поэтому путь движения частиц можно представить в виде отдельных скачков, каждый из которых приводит к преодолению одного барьера.

При вакансионном механизме переноса такой скачок представляет собой перескок частицы из одного узла в другой (вакантный), при междоузловом – скачок из одного междоузлия в другое. Частица при этом совершает путь, длина которого равна либо параметру решетки, либо величине, близкой к нему. Будем рассматривать такой перескок, как элементарный акт самодиффузии.

В кристалле, находящемся в равновесном состоянии перемещения атомов носят случайный, хаотический характер. Тем не менее, час­тицы перемешиваются, вследствие чего происходит их смещение, т.е. диффузия (от лат.: diffusio – распространение). При этом из-за беспорядочного (в изотропной среде – во все стороны равновероят­ного) движения общий путь, совершаемый частицей за единицу време­ни, оказывается намного больше действительного, реального смеще­ния от первоначального ее положения. Учет такого смещения, осно­ванный на статистическом рассмотрении явлений случайных блужда­ний, может быть осуществлен, если просуммировать квадраты длин элементарных путей (скачков), совершенных частицей, т.е. опреде­лить ее суммарное среднеквадратичное смещение от изначального по­ложения. Это можно записать так:

(3.3)

где - суммарное среднеквадратичное смещение частицы; s – длина ее элементарного пути.

Примем для простоты, что

s₁ = s₂ = s₃ = s_i = s, (3.4)

тогда

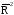= ns², (3.5)

где n - число скачков, совершенных частицей за определенный про­межуток времени.

Условие (3.4) означает, что соотношение (3.5) пригодно для обсуждения явления перескока частиц с изотропных телах, какими являются например кристаллы с кубической решеткой.

Величина учитывает возможное смещение частиц от изначаль­ного положения во всех возможных шести направлениях (вперед и на­зад вдоль каждого из трех направлений трехмерного пространства). Таким образом, лишь шестую часть этой величины можно отнести к одному направлению:

. (3.6)

С другой стороны, среднеквадратичное смещение является функ­цией времени и можно записать, что

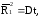(3.7)

где t - общее время дрейфа частицы; D - коэффициент пропорциональности, введенный лишь для соблюдения размерности величин, входящих в соотношение (3.7).

Выясним физический смысл этого коэффициента. Для этого при­равняем (3.6) и (3.7) друг к другу:

Dt = ns²/6. (3.8)