
- •1) Комплексное представление узкополосных сигналов.
- •2) Свойства физической огибающей узкополосного сигнала.
- •3.Равномерное распределение.
- •4.Характеристические функции.
- •1)Статические характеристики в многомерном случае.
- •2)Корреляция.
- •3)Случайный процесс.
- •3)Ансамбли реализации.
- •1.Спектральное представление стационарных случайных процессов.
- •2.Спектральная плотность стационарного случайного процесса.
- •1.Синфазные и квадратурные составляющие.
- •1.Физические системы и их математические модели.
- •1. Системы, описываемые дифференциальным уравнением.
- •2.Собственные колебания динамических систем.
- •3.Усилитель малых сигналов с апериодической нагрузкой.
- •4.Устойчивость динамических систем.
- •2.Резонансный усилитель малых колебаний.
- •3.Многоконтурные частотно – избирательные системы..
- •1.Широкополосные входные воздействия.
- •2.Узкополосные входные воздействия.
- •1.Безынерционные нелинейные преобразования.
- •2.Спектральный состав тока в безынерциальном нелинейном элементе при гармоническом внешнем воздействии.
1.Безынерционные нелинейные преобразования.
При математическом описании такой системы мы сталкиваемся с проблемой решения нелинейных диф. уравнений. Решение таких систем с математической точки зрения известно, однако они довольно сложны. В ряде случаев исследование нелинейных систем удаётся довести до конца простыми способами. Для этого необходимо, чтобы в зависимости (1) не было зависимости от времени. Физически это означает, что безынерциальность элемента.
Внешние характеристики безынерциальности.
Используемые на практике нелинейные элементы имеют разнообразные внешние характеристики. Так можно выделить элементы с однозначными ВАХ и классифицировать характеристики которые содержат участки многозначности.
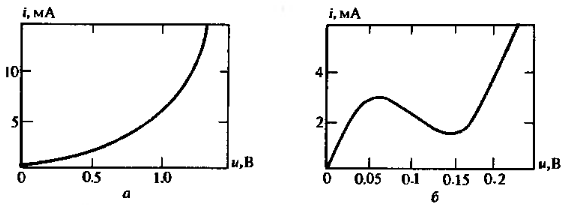
Сопротивление нелинейного двухполюсника.
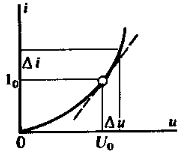
![]() сопротивление постоянного тока.(2)
сопротивление постоянного тока.(2)
![]() (3)
(3)
![]() (4)
– диф. крутизна ВАХ.
(4)
– диф. крутизна ВАХ.
Способы описания характеристик нелинейных элементов.
1.Кусочно-линейная аппроксимация.
Способ основан на замене реальной характеристики двумя или более отрезками.
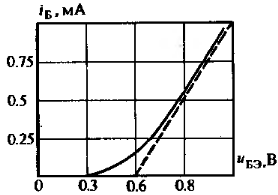
2.Степенная характеристика.
Этот способ основан на разложении ВАХ
в ряд Тейлора, сходящийся в окрестности
рабочей точки
![]() .
.
![]()
Показательная аппроксимация.
Из теории
![]() переходов следует что ВАХ описывается
выражением:
переходов следует что ВАХ описывается
выражением:
![]() (4)
(4)
2.Спектральный состав тока в безынерциальном нелинейном элементе при гармоническом внешнем воздействии.
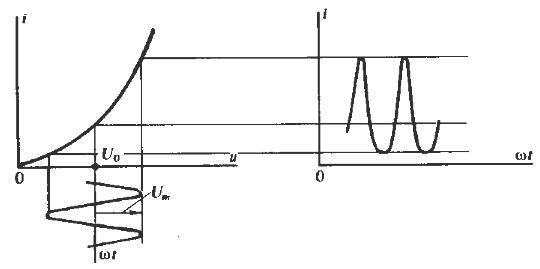
Из построений видно, что одинаковым приращениям напряжения отвечают неодинаковые приращения тока.
Пусть к входным зажимам нелинейного двухполюсника приложен сигнал
![]() (5) введём безразмерную переменную
(5) введём безразмерную переменную
![]() то функция
то функция
![]() (6) периодична относится
(6) периодична относится
![]() и может быть представлена рядом Фурье:
и может быть представлена рядом Фурье:
![]() (7)
(7)
С коэффициентом
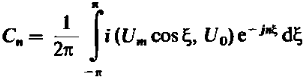 (8)
(8)
Т.к.
![]() чётная, то ряд будет содержать только
cos
чётная, то ряд будет содержать только
cos
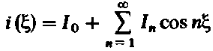 (9)
(9)
Амплитудные коэффициенты гармоник выражается:
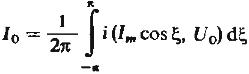 (10)
(10)
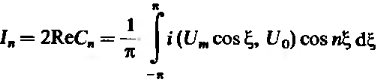 (11)
(11)
И
![]() (12)
(12)
Т.е. сигнал содержит постоянную
составляющую
![]() и бесконечную последовательность
гармоник с амплитудами
и бесконечную последовательность
гармоник с амплитудами
![]()
Пример – кусочно-линейная аппроксимация.
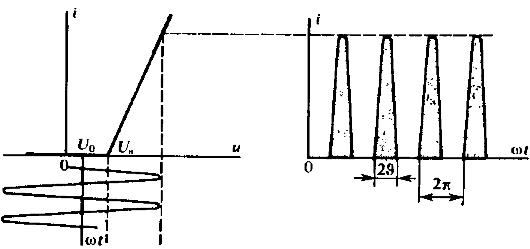
Представим
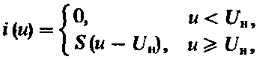
Поданное напряжение:
![]()
Угол отсечки синусов определяется из равенства:
![]()
![]()
Постоянную составляющую амплитуды гармоник тока определяют по формуле:
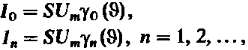
Где
![]() функции Берга.
функции Берга.
Нелинейные искажения в усилителе с резистивной нагрузкой.
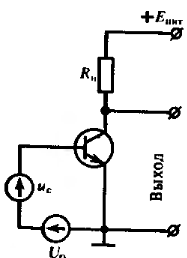
Пусть характер рабочей точки задаётся многочленом 2 степени:
![]()
На входе усилителя напряжение
![]() в коллекторной цепи будем иметь
постоянную составляющую и также токи,
n – гармоники.
в коллекторной цепи будем иметь
постоянную составляющую и также токи,
n – гармоники.
![]() и т.д. вводят величину
и т.д. вводят величину
![]()
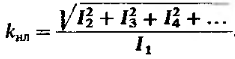 в данном случае
в данном случае
![]()
Коэффициент нелинейных искажений увеличивается с ростом амплитуды сигнала.
