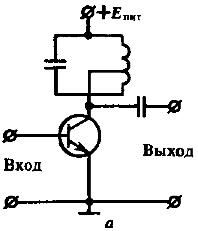
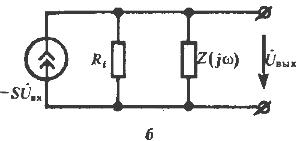
2.Резонансный усилитель малых колебаний.
Отличие от усилителя с резонансно – ёмкостной нагрузкой состоит в том, что нагрузкой прибора служит параллельный колебательный контур, включение контура в общем случае может быть неполным.
(7) преобразуя получаем:
(8)
Где
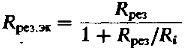(9)
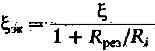(10) можно сказать, что
уменьшает добротность колебательной
системы и становится равной эквивалентной
добротности
(11)
3.Многоконтурные частотно – избирательные системы..
Простейшим многоконтурным частотно – избирательным фильтром является система двух связанных колебательных контуров.
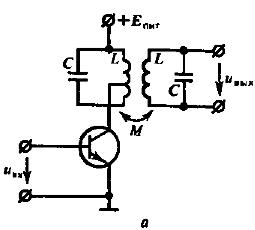
Параметрами этой системы является
коэффициент связи
и фактор связи
.
АЧХ такого усилителя определяется:
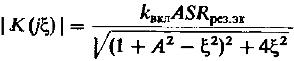(12)
В последнее время в радиотехнике получили распространение активные фильтры.
Идеальные модели частотно – избирательных устройств.
Наиболее простой моделью служит полосовой фильтр.
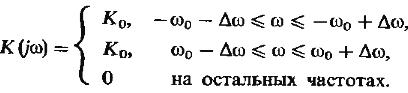
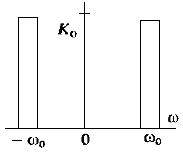
Другой распространенной теоретической моделью узкополосной системы является
Гауссов радиофильтр, АЧХ которого
колоколообразную гауссову кривую,
симметричную относительно частоты
.
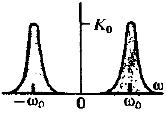
(13)
постоянная величина с размерностью
, определяет частотные свойства фильтра
при
фильтр
узкополосен и эффект перекрытия частотных
характеристик не наблюдается.
Лекция №20
Частотно – избирательные цепи при различных входных воздействиях.
1.Широкополосные входные воздействия.
2.Узкополосные входные воздействия.
Пусть
частотный коэффициент передачи
узкополосной цепи, способный выделить
спектральные составляющие входного
сигнала, сосредоточенные в малых
окрестностях частот
.
Входные колебания Uвх
(t) со спектральной
плотностью
называют широкополосным сигналом
применительно к данной цепи, если функцию
можно приближенно считать постоянной
в пределах полосы пропускания системы
при этом:
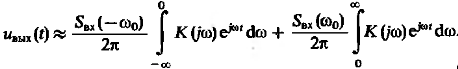(1)
Т.е. форма выходного сигнала определяется не характером входного колебания, а лишь частотным коэффициентом передачи системы.
Импульсная характеристика частотно-избирательной цепи.
Сигнал с определённым широким спектром
является дельта-импульс
выходным сигналом служит импульсная
характеристика:
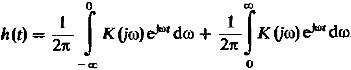(2)
Перейдём к новой переменной
после преобразования можно получить:
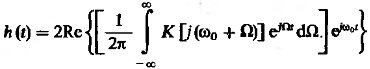(3)
Низкочастотный эквивалент частотно-избирательной цепи.
Этим термином принято называть
воображаемую систему, частотный
коэффициент передачи которой получается
путём смещения частотного коэффициента
передачи реальной узкополосной цепи
из окрестностей частоты
в окрестности нулевой частоты т.е.
(4)
интеграл в (3) является импульсной
характеристикой НЧ – эквивалента.
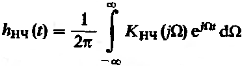(5)
И следовательно:
(6)
Функция
является
комплексной огибающей импульсной
характеристики реальной узкополосной
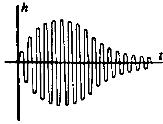
цепи. В соответствии с (6) в общем случае
импульсную характеристику
частотно-избирательной системы
представляет собой квазигармоническое
колебание, огибающая начальная фаза
которого медленно (в масштабе времени
)
изменяется во времени.
Частотно-избирательные цепи при узкополосных входных воздействиях.
Узкополосный сигнал – это когда в
пределах полосы пропускания меняется
.
Пусть входным сигналом служит узкополосное
(квазигармоническое колебание) с
центральной частотой
.
(7)
спектр входного сигнала и его комплексная
огибающая
(8)
Используя спектральный метод и введя
замену переменной
можно после нескольких преобразований
получить
(9) т.е.
(10) спектр плотности огибающей.
Т.е.комплексная огибающая выходного сигнала представляет собой медленно меняющее во времени колебание со спектральной плотностью.
Чтобы решить задачу о прохождении узкополосного сигнала через частотно-избирательную систему следует вначале найти результат воздействия входной комплексной огибающей на НЧ эквивалент исходной системы, а затем перейти к физическому выходному сигналу.
(11)
Равенство (9) соответствует спектральному методу нахождения сигнала на выходе системы в равной мере могут быть использованы и другие известные методы – операторный метод, интеграл. Дюамеля и т.д.
Например по интегралу Дюамеля
(12) где
импульсная характеристика НЧ эквивалента.
Воздействие АМ – сигнала на одноконтурный резонансный усилитель.
Рассмотрим прохождение АМ – сигнала на одноконтурный резонансный усилитель:
(13)
Через одноконтурный резонансный усилитель с частотным коэффициентом передачи.
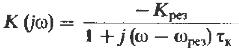(14) допустим, что
, где
-
частота несущее колебание, тогда
(15)
Частотный коэффициент передачи НЧ – эквивалентного усилителя.
(16)
Выходную комплексную огибающую найти из 15. Применив обычный метод комплексных амплитуд.
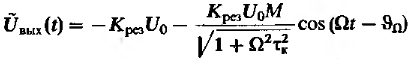(17) где
фазовый сдвиг.
получим:
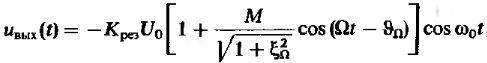(18)
Где
обобщённая
расстройка колебательного контура на
верхней боковой частоте.
На выходе резонансного усилителя существуют колебание, которое будучи усиленным по амплитуде по прежнему является однотональным АМ – сигналом. Однако коэффициент модуляции на выходе меньше, чем на входе:
(19)
Огибающая на выходе запаздывает относительно огибающей входного сигнала на время
.
Лекция №21
Преобразование сигналов в нелинейных радиотехнических цепях.
Наиболее важным свойством линейных
цепей является принцип суперпозиций.
Т.е. гармонический сигнал проходя
линейную цепь не меняет частоту. Это в
значительной мере сужает класс полезных
преобразованных сигналов. Гораздо
большими возможностями обладают
нелинейные системы, в которых зависимость
(1)