1.Физические системы и их математические модели.

Радиотехнические устройства независимо от своего назначения и уровня представляют собой систему т.е. совокупность физических объектов между которыми существует определённые взаимодействия. В структуре системы можно выделить вход на который подаётся исходный сигнал и выход откуда снимается преобразованный сигнал. Если интересуются лишь связью между сигналами на входе и выходе, то говорят, что система представляет собой «черный ящик».

Системные операторы .

В наиболее простом случае как входной сигнал и , называемый откликом или выходной реакцией системы описываются одиночными функциями времени. В общем случае входной и выходной сигналы можно записать:

(1)

Закон связи между сигналами n – мерного Uвх(t) и Uвых(t) задают системным оператором:

(2)

Чтобы полностью определить задачу, следует указать – область допустимых входных воздействий и область выходных сигналов.

Математической моделью системы называют совокупность системного оператора T и двух областей допустимых сигналов .

Стационарные и нестационарные системы.

Система стационарна, если её выходная реакция не зависит от того, в какой момент времени поступает входной сигнал. Т.е. (3) При любых .

Если свойства системы не инвариантны, то систему называют нестационарной системой.

Линейные и нелинейные системы.

Если оператор системы таков, что

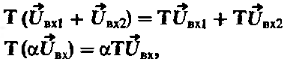(4) и (5)

2.Импульсные, переходные и частотные характеристики линейных стационарных систем.

Импульсной характеристикой – называется функция являющаяся откликом системы на входной сигнал . Т.е. (6)

Т.к. система стационарна, то (7)

Интеграл Дюамеля.

(8)

ИЛИ

(9)

Условие физической реализуемости.

Очевидно, что выходной сигнал, отвечающий импульсному входному взаимодействию, не может возникнуть до момента появления импульса на выходе, т.е.

Т.е. 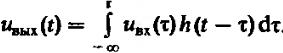(10) физическая система должна быть устойчивой т.е. (11).

Переходная характеристика.

Пусть на входе действует сигнал , функция Хэвисайда. Выходную реакцию (12) между импульсной и переходной характеристикой имеется тесная связь, т.к. ,

То 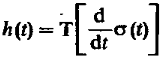(13) или 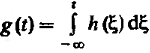(14)

Интеграл Дюамеля можно представить в другой форме:

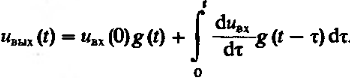(15)

Частотный коэффициент передачи.

При математическом исследовании систем, особый интерес представляют такие входные сигналы, которые будучи преобразованными системой остаются неизменными по форме.

Если имеется равенство:

(16) то Uвх (t) – является собственной функцией системы оператора T, а число - в общем случае комплексное, - его собственным значением.

Покажем, что при любом есть собственная функция линейного стационарного оператора.

(17)

Отсюда видно, что собственным значением системного оператора является комплексное число:

(18) называется – частотным коэффициентом передачи системы .

Частотный коэффициент передачи и импульсная характеристика линейной стационарной системы связаны между собой преобразованием Фурье, т.е.

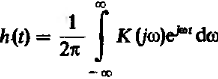(19)

Т.е. любую систему можно рассматривать во временной области с помощью импульсов или переходной характеристики, либо в частотной задавая частотный коэффициент передачи.

Амплитудно – частотная и фазочастотная характеристика.

Можно записать:

(20)

Или

(21)

Амплитудно – частотная характеристика

фазочастотная характеристика

(ФЧХ) – системы.

Критерий Пэли – Винера.

Частотный коэффициент физически реализуемой системы должен быть таким, чтобы существовал интеграл:

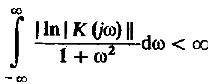(22)

Лекция №18

Воздействие детерминированных сигналов на линейные стационарные цепи.