2.Спектральная плотность стационарного случайного процесса.

Введём функцию - спектральной плотности мощности процесса (спектр мощности).

(6).

Подставив (6) в (4) получаем:

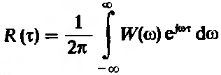(7). Или (8).

Формула (7) и (8) составляют содержание теоремы Винера – Хинчина. Если и поскольку , получаем:

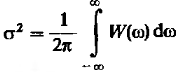(9)

Дисперсия равная средней мощности функций спектрального случайного процесса, есть сумма вкладов от всех участков частотной оси.

Односторонний спектр мощности .

Т.к чётная функция соответствующий спектральной мощности четная функция частоты

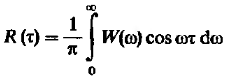(10)

(11)

Введём односторонний спектр мощности:

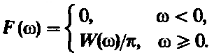(12)

Функция позволяет вычислить дисперсию стационарного случайного процесса, причём интегрированная по положительным частотам :

(13).

В технических расчётах вводят односторонний спектр мощности N (f ) – представляющий собой среднюю мощность случайного процесса, приходящегося на интервал частот шириной в 1кГц.

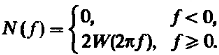при этом легко видеть:

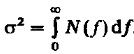(14)

3.Интервал корреляции.

Случайные процессы в радиотехнике обладают следующими свойствами: их функция корреляции стремится к нулю, с увеличением временного сдвига числовой характеристикой для скорости изменения реализации случайного процесса является интервал корреляции .

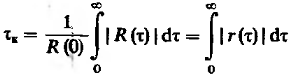(15)

Эффективная ширина спектра.

Рассмотрим выражение:

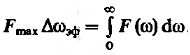(16)

Где односторонний спектр мощности,

экстремальное значение этой функции на интервале

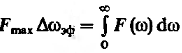(17)

Этой величиной часто пользуются для инженерного расчёта дисперсии шумового сигнала.

4.Белый шум.

В радиотехнике так называется стационарный случайный процесс с постоянной на всех частотах спектральной плотностью мощности:

(18)

Термин «белый шум» подчёркивает аналогию с «белым» (естественным) светом у которого в пределах видимого диапазона интенсивность всех спектральных составляющих одинакова. По теореме Винера – Хинчина:

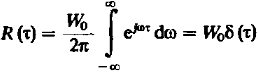(19).

Средняя мощность (дисперсия) белого шума неограниченно велика.

Лекция №16

Узкополосные случайные процессы.

1.Синфазные и квадратурные составляющие.

В радиотехнических задачах важную роль играет особый класс случайных процессов, спектральная плотность мощности которых имеет частоты , отличают от нуля. Функция корреляции узкополосного случайного процесса по теореме Винера – Хинчина

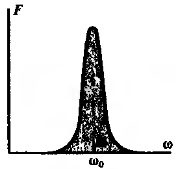
(1) заменим переменную , тогда (2) заменим - на тогда:

(3)

(4) – чётная функция

– нечётная функция.

Удобно ввести нормированную огибающую S ( ) функции корреляции узкополосного случайного процесса определив её тогда (5)

Из 5 следует, что отдельные реализации узкополосного случайного процесса могут представлять квазигармонические колебания:

(6)

У которой огибающая U(t) и начальная фаза (t). Представим 6 как сумму синфазной и квадратурной составляющей:

(7)

Введём случайный процесс Y(t), сопряжённой с исходными процессами X( ). Его реализацией являются преобразования Гильберта.

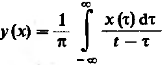(8)

Из 7 и 8 можно получить:

(9)

От туда для мгновенных значений огибающей (10) и начальной фазы:

(11)

Статические свойства сопряженного процесса.

Если то и так же равно нулю, пусть X(t) гауссов процесс, а преобразование Гильберта, то Y(t) – тоже гауссов процесс. Если спектральная плотность реализации x(t), то (12).

Модули спектральной плотности совпадают т.е. отсюда:

(13) и процесс Y(t) – стационарен. Функцию взаимной корреляции можно определить:

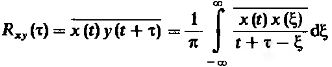
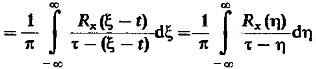(14) – это нечто иное как преобразование Гильберта от X(t).

(15)

(16)

2.Корреляцтонные свойства синфазной и квадратурной амплитуд.

Пусть A(t) и B(t) – выражаются следующим образом:

(17)

Определим корреляцию процесса A.

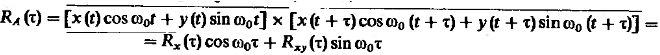(18).

С учётом 2 и 16, 18 можно выразить (19).

Аналогично (20) и (21). Если то (22).

Совместная плотность вероятности и начальная фаза.

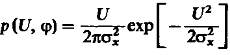(23).

Одномерная плотность вероятности начальной фазы.

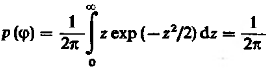где .

Одномерная плотность вероятности огибающей.

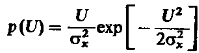(25)

Двумерная плотность вероятности огибающей.

(26)

Где ;

Функция корреляции огибающей.

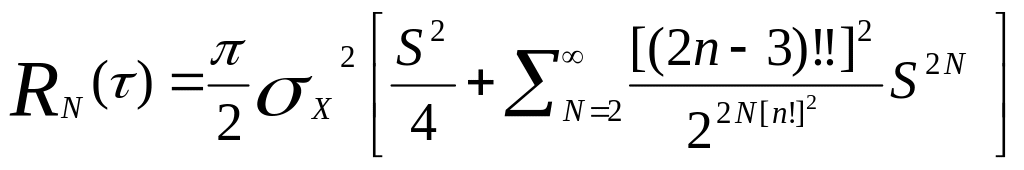(27)

Если то где нормированная функция корреляции огибающей

Огибающая суммы гармонического сигнала и узкополосного нормального шума. Пусть на выходе усилителя есть гаусовский шум и детерминированный сигнал

(28)

Данная формула выражает закон Райса.

Или 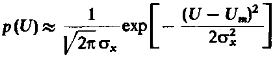(29)

Лекция №17

Методы анализа прохождения детерминированных сигналов через линейные цепи.