3)Ансамбли реализации.

У детерминированных сигналов мы отображаем их функциональными зависимостями или осциллограммами. Если речь идёт о случайных процессах, то ситуация оказывается намного сложнее и мы можем получить лишь единственную реализацию случайного процесса. Случайный процесс представляет собой бесконечную совокупность таких реализаций, образующих ансамбль. Случайные процессы образованные реализациями зависящими от начального конечного числа параметров принято называть – квазидетерминированными процессами.

Плотности вероятности случайных процессов.

Пусть X(t) случайный процесс заданный ансамблем реализации, а - некоторый произвольный момент времени. Фиксируя величины полученные в отдельных реализациях, осуществляем одномерное сечение данного случайного процесса и наблюдаем случайную величину . Её плотность вероятности

называют одномерной плотностью вероятности процесса в момент времени . Согласно определению есть вероятность того что реализация случайного процесса времени примет значение , лежащее в интервале .

Гораздо больше сведений можно получить располагая двумя сечениями случайного процесса в момент времени и

Моментные функции случайных процессов.

Математическое ожидание

(17)

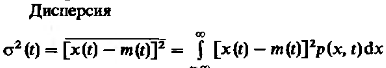(18)

Двумерный центральный момент :

(19)

Стационарные случайные процессы это также случайные процессы статические характеристики которых одинаковы во всех сечениях.

Свойства функции корреляции стационарных процессов.

1) чётность.

2) абсолютные значения этой функции при любых не превышает значения при .

Эргодичность.

Случайный стационарный процесс называют эргодичным, если нахождении его моментных функций усреднение по статическому ансамблю времени. Операция усреднения выполняется над единственной реализацией длительность T которой может быть сколь угодно велика.

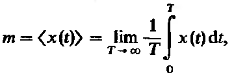(20)

Дисперсия:

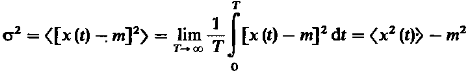(21)

средняя мощность реализации,

мощность постоянной составляющей.

Корреляция.

(22)

Случайный процесс эргодичен, если выполнено условие Слуцкого:

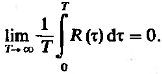(23).

Лекция №15

Корреляционная теория случайных процессов.

1.Спектральное представление стационарных случайных процессов.

Спектральные плотности реализации.

Рассмотрим стационарный случайный процесс X(t), с первым математическим ожиданием Саму функцию модно найти с помощью обратного преобразования Фурье:

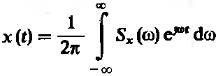(1)

Свойства случайной спектральной.

Усредним значения сигналов по ансамблю реализации:

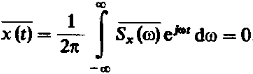(2)

Т.к. сигнал вещественный, то

(3)

И

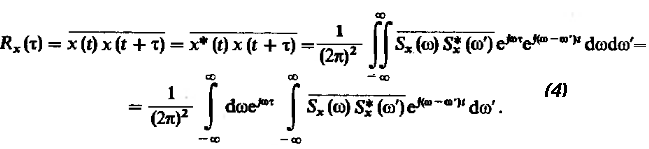
Во внутреннем подынтегральном выражении содержится множитель , который имеет смысл функции корреляции случайной спектральной плотности, чтобы не зависело от t необходимо: (5) такой вид корреляционной связи называется – дельта- коррелированностью.