Лекция №12

Узкополосные сигналы.

Если (t) – низкочастотный сигнал, спектр которого сосредоточен в окрестностях нулевой частоты, то колебание (t) = f (t) cos при достаточно большом значении будет обладать всеми необходимыми признаками узкополосного сигнала, поскольку его спектр окажется сконцентрированным в малых окрестностях точек Узкополосным будет и сигнал , отличающийся фазой «быстрого» сомножителя. Общую модель можно представить:

(1)

Функцию - называют синфазной амплитудой узкополосного сигнала S(t), при заданном значении опорной частоты а его квадратурной амплитудой.

1) Комплексное представление узкополосных сигналов.

Известно, что (2)

- называется комплексной амплитудой гармонического колебания.

Введём комплексную НЧ – функцию:

(3) легко проверить

(4).

Таким образом, комплексная огибающая применительно к узкополосному сигналу играет ту же роль, что и комплексная амплитуда по отношению к простому гармоническому колебанию.

Физическая огибающая, полная фаза и мгновенная частота.

Комплексную огибающую, можно представить в показательной форме:

где (5) U (t) – вещественная неотрицательная функция времени называемая физической огибающей, медленно изменяющаяся во времени начальная фаза узкополосного сигнала. Величины и связаны с синфазной и квадратурной амплитудами соотношениями :

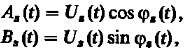(5). Или (5’’) введём полную фазу (6) и определим мгновенную частоту сигнала.

(7)

Из 6 следует, что узкополосный сигнал общего вида представляет собой сложное колебание, получающееся при одновременной модуляции несущего гармонического сигнала, как по амплитуде, так и по фазовому углу.

2) Свойства физической огибающей узкополосного сигнала.

Используя равенства 5 ‘ выразим физическую огибающую через синфазную квадратурную амплитуды: (8)

Комплексная огибающая узкополосного сигнала определяется неоднозначно. Если вместо частоты взять частоту то сигнал S(t) должен быть представлен в виде: (9) и новое значение комплексной огибающей, (10)

Физическая огибающая, являющаяся модулем комплексной огибающей остаётся неизменным, поскольку - имеет единичный модуль.

В каждый момент времени справедливость этого утверждения вытекает из формулы 5”. Знак равенства соответствует моменту времени, когда Но при этом производные сигналы и его огибающей совпадают:

(11)

Важность понятия огибающей обусловлено тем, что в радиотехнике используются специальные устройства – амплитудные детекторы, способные точно воспроизводить огибающую.

Свойства мгновенной частоты узкополосного сигнала

В соответствии с выражением (7) частота узкополосного сигнала постоянна во времени

и можно утверждать что такой сигнал представляет квазигармоническое колебание промодулированное только по амплитуде, в общем случае мгновенная частота изменяется во времени по закону:

(12)

3)Соотношение между спектральным сигналом и его комплексной огибающей.

Пусть спектральная плотность комплексной огибающей узкополосного сигнала S(t), который в свою очередь имеет спектральную плотность S( ).

(13)

Таким образом по известному спектру узкополосного сигнала позволяет найти спектр его комплексной огибающей которая определяет физическую огибающую и мгновенную частоту сигнала.

Лекция №13

Случайные сигналы и их вероятностные характеристики.

В последние десятилетия широкое развитие получила статическая радиотехника. Эта дисциплина рассматривает случаи когда, детерминированное описание сигналов принципиально невозможно.

В радиотехнике случайные сигналы часто имеют вид шумов.

1. Аксиомы теории вероятности:

1)Вероятность не отрицательна и не превышает единицы: (1)

2)Если несовместимые события, то (2);

3)Сумма всех событий, содержащихся в есть достоверное событие:

(3)

Изменение вероятности.

Общепринято оценивать вероятность события относительной частотой благоприятных исходов. Если проведено N – независимых испытаний, причем в n из них наблюдалось, событие A, то эмпирическая (выборочная) оценка вероятности P(A), которую можно получить из этой серии (4).

Функция распределения и плотность вероятности.

Если X – случайная величина т.е. совокупность всевозможных веще6ственных чисел X, принимающих случайные значения . Описание статических свойств X можно получить располагая неслучайной функцией F(x) – вещественного аргумента x, которая равна вероятности того, что случайное число X примет значение, равное или меньше конкретного x.

(5)

Эта функция называется функцией распределения случайной величины X:

(6) – плотность распределения вероятности.

Очевидно, что (7), где p(x)dx – попадания случайной величины X в полуинтервал Если X дискретная случайная величина, принимающая фиксированные значения с вероятностями , то (8)

Во всех случаях плотность вероятности должна быть неотрицательной и удовлетворять условию нормировки:

(9)

2.Усреднение. Моменты случайной величины.

Результатами экспериментов над случайными величинами служат средние значения тех или иных функций от этих величин. Если - известная функция, от X (исхода случайного испытания), то по определению, её среднее значение:

(10)

Наибольший вклад в среднее значение дают те же участки, оси x, где одновременно велики так и плотность вероятности

В статической радиотехнике широко используются особые числовые характеристики случайных величин, называемые моментами. Момент n – го порядка называется средним значением n – ой степени переменной:

(11)

Простейшее математическое ожидание (12)

Средний квадрат случайной величины (13)

Центральные моменты случайных величин задаются общей формулой

(14)

– важнейший центральный момент дисперсии.

(15) очевидно, что

Величина т.е. квадратный корень из дисперсии – называется квадратическим распределением.