Министерство образования и науки Российской Федерации

Муромский институт (филиал)

федерального государственного бюджетного образовательного учреждения

высшего профессионального образования

«Владимирский государственный университет

имени Александра Григорьевича и Николая Григорьевича Столетовых»

ЭКОНОМЕТРИКА

Методические указания

по выполнению практических занятий

и контрольных работ

по дисциплине Эконометрика

для студентов образовательной программы

Составитель:

Мосалёв А.И.

Муром

2012

УДК 330.43(07)

ББК 65в631я7

Э 40

Печатается по решению редакционно-издательского совета

Муромского института (филиала)

Владимирского государственного университета имени Александра Григорьевича

и Николая Григорьевича Столетовых

Э 40 Эконометрика: метод. указания к практическим занятиям по дисциплине Эконометрика для студентов образовательной программы / сост.: А.И. Мосалёв. – Муром: Изд.-полиграфический центр МИ ВлГУ, 2010. - с.

Содержит основной материал практического применения инструментов эконометрики для исследования экономических процессов и явлений с целью дальнейшего анализа возможных событий в будущем. Приведены варианты решения задач, а также представлен материал для самостоятельного решения.

УДК 330.43(07)

ББК 65в631я7

© Муромский институт (филиал)

государственного образовательного учреждения

высшего профессионального образования

« Владимирский государственный университет», 2012

Содержание

ПАРНЫЕ РЕГРЕССИОННЫЕ МОДЕЛИ

МНОЖЕСТВЕННАЯ РЕГРЕССИЯ

ЗАДАНИЯ ПО ВАРИАНТАМ

Вопросы для рассмотрения

Практическая часть

ЛИТЕРАТУРА

ПРИЛОЖЕНИЯ

№ 1. ПАРНЫЕ РЕГРЕССИОННЫЕ МОДЕЛИ

Существуют два варианта взаимосвязи между переменными x и y:

1. х и у равноценные, при этом основным является вопрос по наличии и силе взаимосвязи между Х и У.

Например Х – доходность акций, У – доходность облигаций.

Х – доходность ПИФа, У – доходность обезличенного вклада.

При исследовании зависимости между такими переменными используется корреляционный анализ, основная мера которого

Если r_x,y = -1, то x и y связаны отрицательной линейной зависимостью. Если r_x,y =1, то х и у связаны положительной линейной зависимостью. Если r_x,y =0, то между х и у отсутствует связь.

2. Х и У связаны зависимостью. Если х – независимая переменная, а У – зависимая переменная, тогда изменение Х обязательно влечёт изменение У.

Например: Х – доход компании, У – вкладывание средств в активы предприятия, тогда Х↑→У↑.

Х – цена, У – спрос, тогда Х↑→У↓.

Х – курс волют, У – объём чистого экспорта: Х↓→У↓.

Однако, такие зависимости неоднозначные, так как каждому конкретному значению объясняющей переменной Х соответствует некоторое вероятностное распределение зависимой переменной У, поэтому анализируется, как переменная Х влияет на среднее значение зависимой переменной.

- такая зависимость называется функцией регрессии Y на Х.

Регрессия – это функциональная зависимость между объясняющими переменными и условным математическим ожиданием зависимой переменной, которая строится с целью прогнозирования этого среднего значения при фиксированных значениях объясняющей переменной.

В регрессионных моделях обязательно включаются случайная переменная ε, определяющая случайный характер регрессионной связи,

.

Причины наличия ε в регрессионных уравнениях:

- не включение в модель всех объясняющих переменных;

- неправильный выбор функциональной формы модели;

- агрегирование переменных (т.е. в зависимости используются факторы, которые сами являются сложными комбинациями более простых переменных, например совокупный спрос, как комбинация индивидуальных спросов);

- ошибки измерений;

- ограниченность статистических данных;

- непредсказуемость человеческого фактора – эта причина может испортить самую качественную модель, так как невозможно спрогнозировать поведение каждого отдельного человека.

Этапы построение регрессионной модели:

1. этап спецификации – в случае парной регрессии выбор формулы осуществляется по графическому изображению реальных статистических данных в виде точек в декартовой системе координат, которая называется корреляционной формой или диаграммой рассеивания.

xi	x1	x2	…	xn
yi	y1	y2	…	yn

рисунок 1. рисунок 2. рисунок 3

рисунок 4. рисунок 5. рисунок 6.

рисунок 7.

рисунок 1 – связь близка к линейной, поэтому функцию регрессии выбираем в виде ;

рисунок 2 - - параболическая зависимость (полином второго порядка);

рисунок 3 – явная взаимосвязь между х и у отсутствует, поэтому какую бы ни выбрали форму связи, результат спецификации и параметризации будет неудачным;

рисунок 4 – зависимость описывается уравнением равносторонней гиперболы ;

рисунок 5 – связь с логлинейным распределением (степенное уравнение парной регрессии) ;

рисунок 6 – связь описывается показательным уравнением ;

рисунок 7 – представлен полином третьего порядка, уравнение которого выглядит следующим образом

Существуют и другие уравнения, описывающие однофакторную регрессионную зависимость. Среди них выделяются:

1) экспоненциальное уравнение бывает двух видов:

2) логарифмическое (полулогарифмическое) уравнение парной регрессии:

3) обратное уравнение парной регрессии

.

2. Этап параметризации – находятся численные значения параметров регрессии функции a, b, c, при использовании метода наименьших квадратов;

3. Этап верификации – проверяется качество найденных параметров: оценивается их точность, статистическая значимость, находятся их доверительные интервалы, а также оценивается общее качество уравнения регрессии по численному значению коэффициента детерминации.

Для решения задач в эконометрике используется метод наименьших квадратов, суть которого заключается в определении оценок предложенного уравнения регрессии.

Для работы с регрессионным анализом следует проводить следующие шаги:

Этап 1.

Определение параметров a и b производится по следующей системе уравнений:

.

Этап 2.

После того, как уравнение регрессии составлено, необходимо провести степень согласованности параметров X и Y между собой. Для этого используется коэффициент корреляции:

,

где σ (x) и σ (y) – среднеквадратические отклонения параметров, определить значения которых можно следующим образом:

,

где D (x) и D(y) – дисперсии параметров рядов динамики, значения которых определяются следующим образом:

.

Связи между параметрами может быть обратной (при r_xy < 0), слабой (0,5 >r_xy >0), так и тесной (r_xy ≈ 1).

Этап 3.

Следующим этапом является определение точности оценок коэффициента регрессии – стандартных ошибок (S) коэффициентов регрессии a и b.

Стандартная ошибка регрессии определяется по следующей формуле (на основе отклонения ε):

.

Ошибки параметров a и b определяются по формулам:

,

или

;

или

.

Этап 4.

Следующим шагом является проверка статистической значимости коэффициентов регрессии.

Для этого применяется проверка статистических гипотез:

Гипотеза H₀ при b = 0, следовательно гипотеза H₀ нулевая.

Гипотеза H₁ при b ≠ 0, следовательно гипотеза H₁ альтернативная.

Если гипотеза H₀ принимается, то это означает, что параметр Y не зависит от X и b статистически не значим. Это указывает на наличие зависимости между X и Y.

Для проверки гипотезы составляется статистика:

,

которая, при справедливости H₀, имеет распределение Стьюдента (см. приложения) с числом степеней свободы n-2.

Для проведения вычисляется t наблюдаемая, которая сравнивается с t критической.

Для расчёта критического значения t статистики используется следующая формула:

со степенью свободы n-2.

α – уровень значимости.

Если t_набл. > t_кр., то H₀ отклоняется.

По аналогичной схеме проверяется гипотеза о статистической значимости параметра уравнения регрессии a, только для определения значения статистики t используется следующая формула:

.

Если выполняется условие, что t_набл. < t_кр., то H₀ принимается и оцениваемым параметром можно пренебречь в уравнении регрессии.

Этап 5.

Следующим этапом является определение интервальных оценок теоретических коэффициентов регрессии.

Для этого составляются следующие статистики:

и

,

которые имеют распределение Стьюдента с числом степеней свободы n-2.

Для (1-α) доверительного интервала по таблицам критических распределений Стьюдента по доверительной вероятности γ=1-α определяются критические значения , n-2, удовлетворяющая условию:

.

Границы доверительного интервала определяются следующим образом:

.

Если преобразовать представленный выше интервал к значениям коэффициентов регрессионного уравнения, то получим:

Этап 6.

Следующим этапом является определение общего качества уравнения регрессии.

Для этого определения используется коэффициент детерминации:

Коэффициент детерминации определяет долю разброса зависимой переменной, объясняемой регрессией Y на X.

Коэффициент детерминации находится в следующих пределах:

0≤R²≤1.

Близость коэффициента детерминации к единице характеризует общее качество уравнения регрессии как высокое.

Значение коэффициента детерминации должно равняться квадрату коэффициента корреляции, т.е. R² = (r_xy)².

Этап 7.

Следующей стадией является проведение анализа полученного коэффициента детерминации по критерию Фишера (F статистика).

Критерий Фишера определяется как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещённой оценкой дисперсии остаточной последовательности для рабочей модели.

F – критерий Фишера выглядит следующим образом:

,

где значение r² = R².

Далее, определяются распределения для заданного уровня значимости по таблицам Фишера (см. приложение).

В том случае, если фактическое значение F критерия меньше табличного, то это даёт основание отклонить нулевую гипотезу H₀.

В противном случае, нулевая гипотеза отклоняется с вероятностью 1-α, принимается альтернативная гипотеза H₁ о статистической значимости анализируемой модели.

Если F > F_кр., то коэффициент детерминации статистически значим и это говорит о надёжности самого уравнения регрессии.

Этап 8.

Следующим шагом является определение доверительных интервалов для зависимой переменной.

В данном случае используется два подхода для прогнозирования индивидуального значения зависимой переменной.

Первый подход – составляется статистика, вида:

,

Которое имеет распределение Стьюдента с числом степеней свободы n-2.

По таблицам критических распределений Стьюдента определяется критическое значение , n-2, удовлетворяющее условию:

.

Если преобразовать представленный выше интервал к значениям a и b, то получим:

Доверительный интервал для среднего значения S(Y_P) зависимой переменной, покрывающий теоретическое значение с вероятностью 1-α определяется по формуле:

.

Второй подход – прогнозирование индивидуальных значений зависимой переменной. Построение формулы для данного подхода аналогично первому подходу, только:

Этап 9.

Определение ошибки аппроксимации.

Ошибка аппроксимации представляет собой величину отклонений фактических значений от расчётных результативного признака (y-ŷ_x) по каждому наблюдению.

Средняя ошибка аппроксимации может быть определена по следующей формуле:

В случае если ошибка аппроксимации не превышает 8-10%, модель, подобранная для прогноза считается достаточно качественной.

В любом случае, предпочтение должно быть отдано той модели, значение ошибки аппроксимации которой - наименьшее.

Этап 10.

На данном этапе рассчитывается коэффициент эластичности:

.

Смысл данного коэффициента заключается в следующем – он показывает, на сколько процентов изменится Y в среднем по совокупности от своей величины при изменении фактора X на 1% от своего среднего значения.

Этап 11.

Следует провести анализ на гетероскедастичность. Предпосылкой МНК является условие постоянства случайных отклонений, которую называют гомоскедастичностью. Не должно быть безоговорочной причины, которая вызывала бы большое отклонение при одних наблюдениях и меньшее – при прочих. Невыполнение такой предпосылки называют гетероскедастичностью.

Одним из методов определения наличия гетероскедастичности является тест ранговой корреляции Спирмена.

,

где d – разность между значениями переменной x и |e_i|

Доверительная вероятность выглядит следующим образом:

.

По табличным t определяется граничная точка t_α;n-2.

Статистика t рассчитывается по уравнению:

.

Если t< t_α;n-2, то на уровне значимости α принимается гипотеза об отсутствии гетероскедастичности. В ином случае гипотеза отклоняется.

В модели с несколькими факторами, проверка гипотезы об отсутствии гетероскедастичности проводится с помощью статистики t для каждого из них в отдельности.

№ 2. МНОЖЕСТВЕННАЯ РЕГРЕССИЯ

Как правило, в экономике и менеджменте, на исследуемый показатель может оказывать влияние не один фактор, а сразу несколько.

К примеру, курсовая стоимость волюты на фондовых биржах может зависеть не только от инфляции, но и уровня занятости населения, геополитических факторов и пр.

Модель множественной линейной регрессии выглядит следующим образом:

Как и в случае с парной регрессией, множественная регрессия может описываться и линейной, и степенной, и экспоненциальной, и гиперболической функциями.

Исследование необходимо проводить в следующей последовательности:

Этап 1.

Определяются оценки параметров регрессии. Для этого используется следующая система уравнений:

Этап 2.

Рассчитываются коэффициенты с некоторыми независимыми переменными по формулам:

1) коэффициент частной корреляции между y и x_m при исключении влияния предшествующего x:

,

2) коэффициент частной корреляции между y и x₁ при исключении влияния x₂:

,

3) коэффициент частной корреляции между y и x₂ при исключении влияния x₁:

,

4) коэффициент частной корреляции между всеми параметрами x при исключении влияния y:

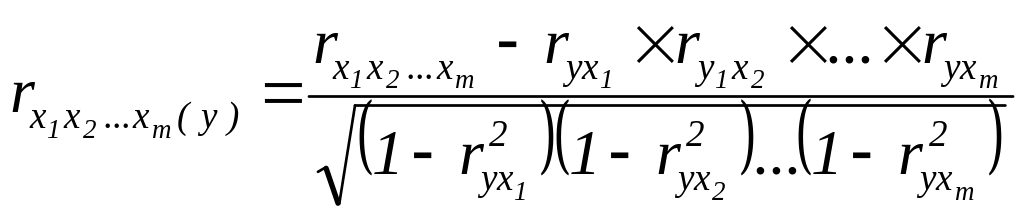
Этап 3.

Проверяется статистическая значимость коэффициентов корреляции, строится гипотеза о равенстве нолю.

H₀: r_yxi(x₁x₂…x_m)=0

Таким образом, статистика t рассчитывается следующим образом:

.

Значимость частного коэффициента корреляции проверяется по схеме, описанной для парных регрессионных моделей и сравнивается:

, где

t_ε – табличное значение с числом степеней свободы n-(m+1).

Выделяются следующие пределы значимости параметров модели:

- если /t/≤1, то параметр статистически не значим;

- если 1≤/t/<2, то параметр значим относительно;

- если 3</t/≤3, то параметр значим;

- если /t/>3, то исключать параметр из модели нельзя, так как его значимость высока, а вероятность ошибки не превышает 0,1%.

Этап 4.

После расчёта всех необходимых коэффициентов корреляции и вычисления, соответствующих им t-статистик, составляется матрица парных линейных коэффициентов корреляции:

.

Этап 5.

Проводится расчёт коэффициента детерминации, который выглядит следующим образом:

.

Однако для множественной регрессии следует применять скорректированный коэффициент детерминации, который рассчитывается следующим образом:

.

Этап 6.

Следующим шагом является определение значимости коэффициента детерминации посредством F статистики Фишера.

Прежде всего, определяется значимость общего коэффициента детерминации. Для этого составляется гипотеза:

H₀:β₁=β₂=…=β_m=0.

Используется соотношение:

,

удовлетворяющее F распределению Фишера с числом степеней свободы n-(m+1), где

n – число переменных в исходной таблице.

m – число объясняющих переменных.

В том случае, если фактическое значение F критерия меньше табличного, то это даёт основание отклонить нулевую гипотезу H₀.

В противном случае, нулевая гипотеза отклоняется, принимается альтернативная гипотеза H₁ о статистической значимости.

Если F > F_кр., то коэффициент детерминации статистически значим и это говорит о надёжности самого уравнения регрессии.

Этап 7.

Проверяется выполняемость предпосылок метода наименьших квадратов. Для этой цели используется статистика Дарбина-Уотсона (DW):

.

В определении статистика Дарбина-Уотсона используются верхний (d_U) и нижний (d_L) пределы уровней значимости.

В зависимости от параметров статистики DW, выделяются различные решения относительно гипотез, которые представлены на рисунке:

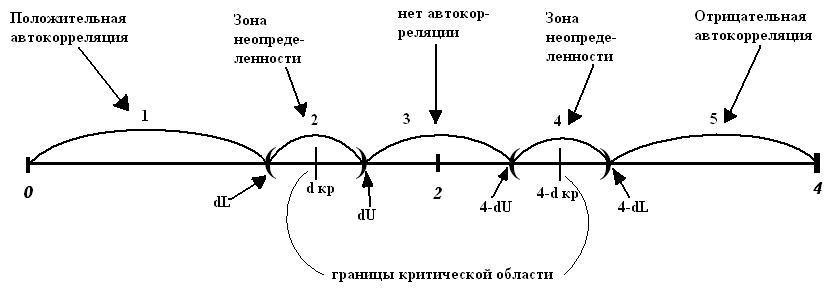
1. DW<d_L – нулевая гипотеза (H₀) отвергается в пользу гипотезы о положительной автокорреляции остатков.

2. d_L<DW<d_U – гипотеза H₀ не принимается и не отвергается.

3. d_U<DW<2; 2<DW<(4-d_U) – гипотеза H₀ принимается.

4. (4-d_U)<DW<(4-d_L) – гипотеза H₀ не принимается и не отвергается.

5. DW>(4-d_L) – гипотеза H₀ отвергается в пользу гипотезы от отрицательной автокорреляции остатков. В этом случае необходимо провести дополнительные исследования с увеличением объёма статистических данных.

Метод DW применяется для обнаружения автокорреляции первого порядка (ситуация, при которой коррелируются случайные члены регрессии в последовательных наблюдениях).

Причина выявления автокорреляции остатков заключается в том, что если использовать обыкновенный метод наименьших квадратов, то выборочные дисперсии оценок коэффициентов будут больше, по сравнению с альтернативными методами оценивания; стандартные ошибки коэффициентов будут оценены неправильно; прогнозы по полученной модели будут не достоверными.

Этап 8.

В случае если выявлено наличие автокорреляции, её можно устранить. Делается это посредством следующих методов:

- включение в модель отсутствующую, но важную объясняющую переменную;

- изменить форму зависимости;

- произвести авторегрессионное преобразование.

Авторегрессионное преобразование проводится следующим образом. Переменные уравнения x и y заменяются на x^* и y^*, значения которых вычисляются по правилу:

i=2,…,n

.

Поправки Прайса-Винстена:

Этап 9.

Следует провести анализ на гетероскедастичность. Предпосылкой МНК является условие постоянства случайных отклонений, которую называют гомоскедастичностью. Не должно быть безоговорочной причины, которая вызывала бы большое отклонение при одних наблюдениях и меньшее – при прочих. Невыполнение такой предпосылки называют гетероскедастичностью.

Одним из методов определения наличия гетероскедастичности является тест ранговой корреляции Спирмена.

.

Доверительная вероятность выглядит следующим образом:

.

По табличным t определяется граничная точка t_α;n-2.

Статистика t рассчитывается по уравнению:

.

Если t< t_α;n-2, то на уровне значимости α принимается гипотеза об отсутствии гетероскедастичности. В ином случае гипотеза отклоняется.

В модели с несколькими факторами, проверка гипотезы об отсутствии гетероскедастичности проводится с помощью статистики t для каждого из них в отдельности.