Лекция 4
Цикл с предусловием (продолжение)
2. Найти сумму с абсолютной погрешностью не хуже .
В примере речь
идёт о нахождении суммы, содержащей
бесконечное количество слагаемых. В
математическом анализе для такой суммы,
называемой суммой ряда,
строится доказательство того, что она
конечна при любом комплексном
.
В отличие от изученной в школе суммы
бесконечной убывающей геометрической
прогрессии, данная сумма
не может быть вычислена по короткой
формуле, и вообще не может быть вычислена
точно. Речь может идти только о приближённом
вычислении
,
правда, со сколь угодно малой погрешностью.
Пусть натуральное
есть количество первых слагаемых,
которые мы намерены «удержать» в сумме.
Тогда
.
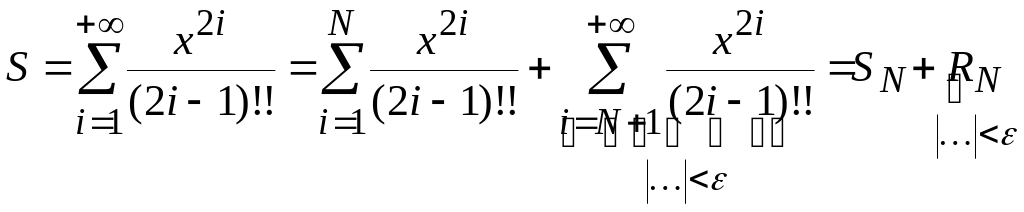Величины
и
имеют названия соответственно частичная
сумма и остаток ряда. Если пренебречь
ошибками округления, т.е. считать, что
величина
может быть найдена точно, погрешность
будет выражаться величиной
.
Найти погрешность невозможно, но можно
её модуль оценить «сверху». Остаётся
выяснить, при каком
есть возможность гарантировать, что
.
Искомое должно будет подчиняться двум требованиям. Первое из них,
,
(1)
будет выполнено
при
.
Далее проведём намеченную оценку
«сверху»:
,
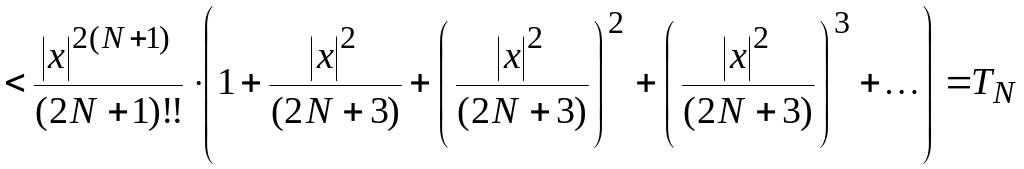где
.
Сумма, стоящая в последних высоких (внешних) скобках, есть сумма бесконечно убывающей геометрической прогрессии (в силу (1)), и к ней применена соответствующая школьная формула.
Теперь гарантировать, что , можно при таком , когда
.
(2)
Величина
стремится к нулю с ростом
монотонно при соблюдении (1). Таким
образом, если достигнуто такое
,
при котором выполняются неравенства
(1) и (2), то
выражает искомую сумму с погрешностью
не хуже, чем
.
S0 = 0 |
|
A1 = x2 |
S1 = S0 + A1 |
B1 = A1*x2/3 |
A2 = B1 |
S2 = S1 + A2 |
B2 = A2*x2/5 |
A3 = B2 |
. . . |
. . . |
. . . |
Si = Si–1 + Ai |
Bi = Ai*x2/(2*i+1) |
Ai+1 =Bi |
Программная реализация примера предлагается в виде метода:
static double F(double x, double Eps)
{
int i; double x2, S, A, B, R;
x2 = x * x;
A = x2;
S = 0;
i = 1;
if (Eps <= 0 || Eps >= 1) return 0;
R = 2 * Eps;
while (x2 >= 2 * i + 3 || R >= Eps)
{
B = A * x2 / (2 * i + 1);
S += A;
A = B;
R = B / (1 – x2 / (2 * i++ + 3));
}
return S;
}
В показанном коде имеется три момента, заслуживающих обсуждения.
1. Оператор R = 2 * Eps введён для того, чтобы первый тест на продолжение гарантированно дал true.
2. Сравнение x2 / (2 * i + 3) >= 1 заменено сравнением x2 >= 2 * i + 3. Эти два сравнения эквивалентны по значению, но второе выполняется быстрее, поскольку в нём нет «тяжёлой» арифметической операции деления.
3. Следующие два фрагмента программы
R = B / (1 – x2 / (2 * i++ + 3)); |
R = B / (1 – x2 / (2 * i + 3)); i++; |
эквивалентны по численным результатам, однако, первый из них выполняется быстрее, поскольку в нём переменная i извлекается из памяти в регистр только один раз. В первом столбце применён постфиксный инкремент переменной i, то есть значение этой переменной сначала применено для вычисления R, и только потом наращено на единицу. Простая замена постфиксного инкремента на префиксный дала бы совершенно другой, неверный результат. Разумеется, оператор с префиксным инкрементом
R = B / (1 – x2 / (2 * ++i + 1))
был бы верным, но код потерял бы наглядность.
Цикл с постусловием
<Цикл с постусловием> ::= do <Оператор> while (<Тест на продолжение>)
<Оператор> есть тело цикла, которое хотя бы один раз будет выполнено.
<Тест на продолжение> есть логическое выражение. Если оно принимает значение false, цикл будет прекращен. Если true, <Оператор> будет в очередной раз выполнен, после чего вновь буде проведён <Тест на продолжение>, и т.д. Если тест даёт результат false при первой же оценке, то тело цикла выполнится, отличие от цикла с предусловием, один раз. Если он даёт true при каждой оценке, то тело цикла выполняется неограниченно много раз.
Примеры