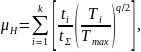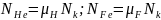- •Иркутский государственный технический университет
- •664074, Иркутск, ул. Лермонтова, 83
- •Введение
- •1 Выбор материала зубчатых колес, термической обработки, твёрдости и определение допускаемых напряжений
- •1.1 Материалы зубчатых колес
- •1.2 Термическая и химико-термическая обработка сталей
- •1.3 Наиболее распространенные варианты термической обработки
- •1.4 Внешняя нагрузка и кривая усталости
- •1.5 Определение допускаемых контактных напряжений при постоянном режиме нагружения
- •1.6 Определение допускаемых напряжений изгиба при постоянном режиме нагружения
- •1.7 Определение допускаемых напряжений при переменном режиме нагружения
- •1.8 Типовые режимы нагружения
- •1.9 Последовательность определения допускаемых напряжений
- •1.10 Пример определения допускаемых напряжений
- •2 Проектировочный расчет цилиндрической зубчатой передачи
- •2.1 Силы, действующие в зацеплении цилиндрических зубчатых колес
- •Распределение нагрузки в зубчатых передачах
- •Коэффициент концентрации нагрузки при расчете контактных напряжений
- •Коэффициент концентрации нагрузки при расчете напряжений изгиба
- •Коэффициент динамической нагрузки при расчете контактных напряжений
- •Коэффициент динамической нагрузки при расчете изгибных напряжений
- •(Для многопарного зацепления)
- •Причины разрушения и критерии расчета зубчатых передач
- •Расчет цилиндрических передач на контактную прочность
- •Расчет цилиндрических передач на прочность при изгибе
- •Пример проектировочного расчета цилиндрической косозубой передачи внешнего зацепления
- •Определение величины межосевого расстояния из расчета прочности по контактным напряжениям
- •Определение значения модуля из расчета прочности по напряжениям изгиба
- •Расчет коэффициентов динамичности нагрузки
- •Проверка выполнения условия прочности по контактным напряжениям
- •Проверка выполнения условия прочности по напряжениям изгиба
- •Список литературы
1.7 Определение допускаемых напряжений при переменном режиме нагружения
Большинство зубчатых передач работает при переменных режимах нагружения. График нагрузки (см. рис. 1.3, б) имеет несколько ступеней, и на каждой i –ой ступени действует постоянный момент Ti в течении Ni циклов перемены напряжений. Возможные в эксплуатации пиковые моменты (например, при пуске) являются кратковременно действующими, их не учитывают в расчетах на сопротивление усталости.
Из опыта известно, что разрушение детали при периодическом нагружении с постоянными параметрами циклами напряжений (работа на одной ступени) происходит в соответствии с кривой усталости (рис. 1.7).
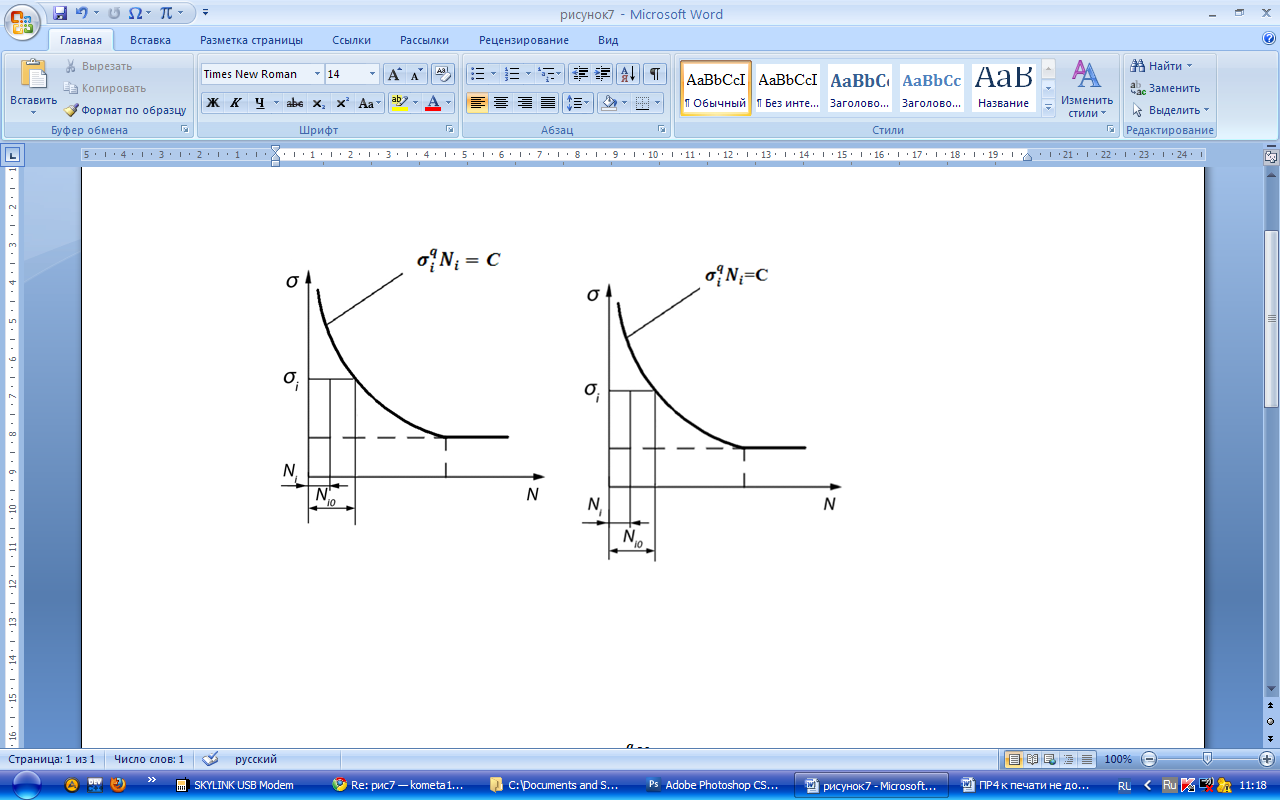 Если
число циклов действия напряжения
Если
число циклов действия напряжения
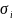 в
i
– ом режиме нагружения равно
,
а полное число циклов нагружения (за
все время работы до разрушения) при
данном уровне напряжений –
в
i
– ом режиме нагружения равно
,
а полное число циклов нагружения (за
все время работы до разрушения) при
данном уровне напряжений –
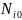 ,то
отношение
,то
отношение
 определяет часть прочности, потерянной
при действии напряжений
.
Тогда
степень полученных повреждений детали
при работе i
–ой
ступени можно оценить относительной
долговечностью
.
определяет часть прочности, потерянной
при действии напряжений
.
Тогда
степень полученных повреждений детали
при работе i
–ой
ступени можно оценить относительной
долговечностью
.
Рис. 1.7
Экспериментально установлено, что при работе на нескольких ступенях нагружения повреждения продолжают независимо нарастать пропорционально относительной долговечности и поэтому их можно линейно суммировать. Согласно этой гипотезе линейного суммирования усталостных повреждений, разрушение произойдет, когда сумма относительны долговечностей достигнет единицы:
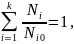
где k – число режимов нагружения.
Выражение
под знаком суммы умножим и разделим на
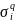 :
:
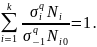
Величина
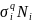 в
соответствии с уравнением кривой
усталости является постоянной и ее
можно вынести за знак суммы:
в
соответствии с уравнением кривой
усталости является постоянной и ее
можно вынести за знак суммы:

а
затем запишем через параметры
 и
и
 эквивалентного
постоянного режима нагружения
эквивалентного
постоянного режима нагружения
-

(1.9)
Таким образом, реальному переменному режиму нагружения можно поставить в соответствие эквивалентный постоянный режим, на котором деталь приобретает ту же степень усталостного повреждения.
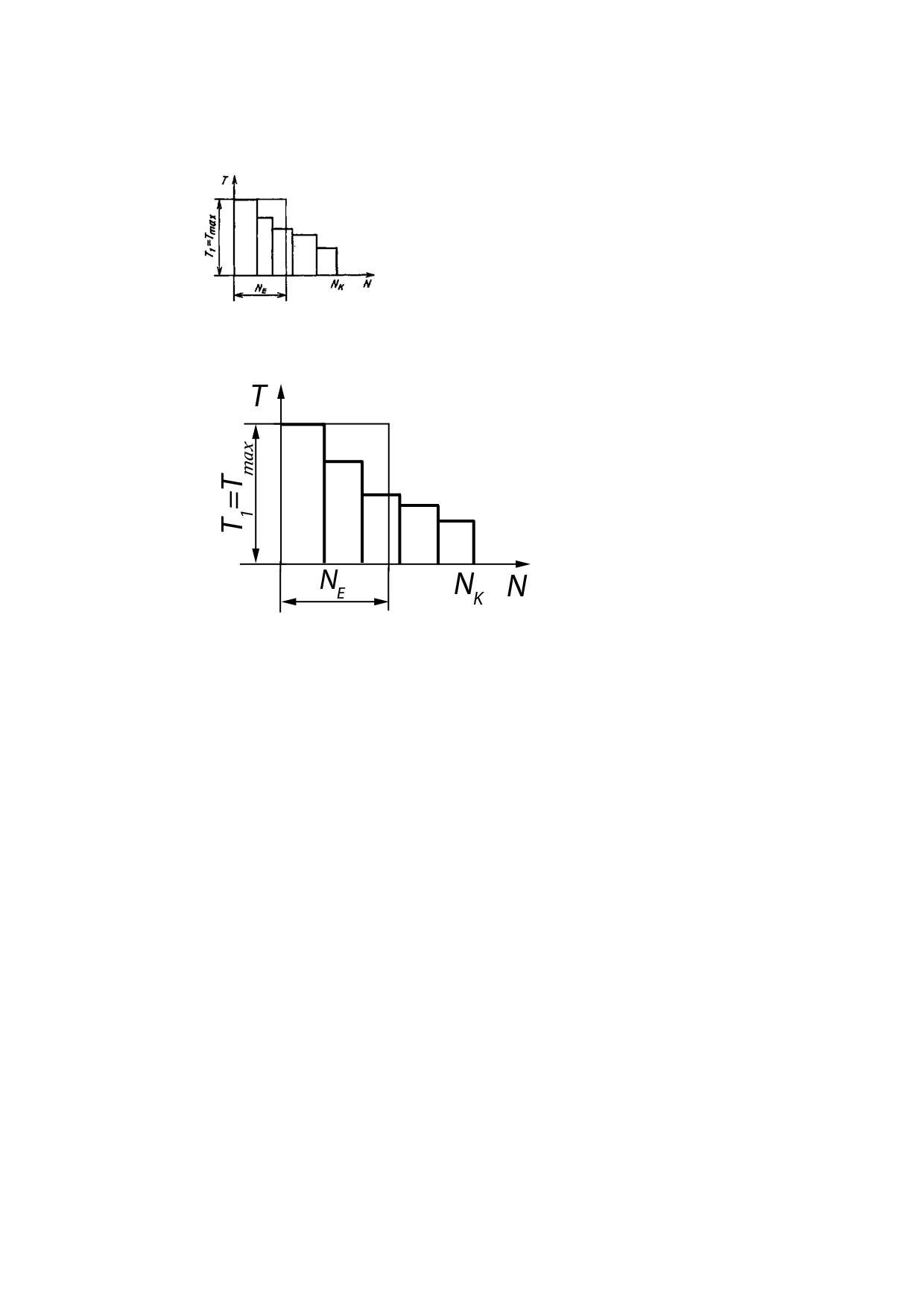 В
качестве эквивалентного принимают
постоянный режим с номинальным
моментом
В
качестве эквивалентного принимают
постоянный режим с номинальным
моментом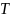 (наибольшим
из длительно действующих
(наибольшим
из длительно действующих
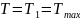 ),
вызывающим действие напряжений и
эквивалентным числом циклов вызывающим
действие напряжений
и эквивалентным числом циклов нагружения
(рис.
1.8).
),
вызывающим действие напряжений и
эквивалентным числом циклов вызывающим
действие напряжений
и эквивалентным числом циклов нагружения
(рис.
1.8).
Из
соотношения (1.9) получаем зависимость
для вычисления эквивалентного числа
циклов перемены напряжений
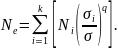
Рис. 1.8
Выразим
число циклов
перемены
напряжений на i
– ом уровне нагружения через
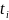 и
примем частоту вращения на всех уровнях
нагрузки одинаковой
и
примем частоту вращения на всех уровнях
нагрузки одинаковой
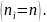 Тогда
выражение для эквивалентного числа
циклов нагружения перепишем в виде
Тогда
выражение для эквивалентного числа
циклов нагружения перепишем в виде
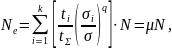
где –
коэффициент приведения переменного
режима работы к постоянному
–
коэффициент приведения переменного
режима работы к постоянному
 Известно,
что контактные напряжения пропорциональны
степени 0,5 нагрузки, а напряжения изгиба
пропорциональны первой степени нагрузки.
Заменяя напряжения через вращающие
моменты коэффициенты приведения
напряжений:
Известно,
что контактные напряжения пропорциональны
степени 0,5 нагрузки, а напряжения изгиба
пропорциональны первой степени нагрузки.
Заменяя напряжения через вращающие
моменты коэффициенты приведения
напряжений:
для контактных напряжений
|
(1.10) |
для изгибных напряжений
|
(1.11)
|
Таким образом, расчет допускаемых напряжений при переменных режимах нагружения проводят по формулам для постоянного режима с заменой числа циклов на эквивалентные числа циклов:
|
(1.12) |
на контактную прочность и изгибную прочность соответственно.