Расчет цилиндрических передач на прочность при изгибе
Установлено, что разрушение, приводящее к излому зуба, всегда начинается в зоне действия напряжений растяжения, причем наибольшие напряжения изгиба возникают в момент начала контакта зубьев. Поэтому все вычисления выполняем для зоны растяжения и момента начала контакта.
В
качестве модели зуба выберем жестко
закрепленную у основания балку,
нагруженную моментом изгиба
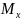и сжимающей нормальной силой
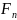(рис. 2.4,а) предположим также, что нагрузка
полностью воспринимается только одним
зубом и прикладывается
статически. Это в данном случае означает,
что коэффициент перекрытия считается
равным единице, причем при фактической
работе передачи не возникает динамических
нагрузок.
Сечение
зуба у основания представляет собой
прямоугольник (рис. 2.4,б), ширину которого
обозначим через
,
а длину – через
,
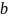так что его площадь равна
.
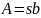Такое сечение, с точки зрения прочности,
называется опасным сечением. Заметим,
что размеры
и
можно трактовать как толщину зуба и
ширину колеса соответственно.
Если
угол наклона силы
относительно основания зуба обозначить
через
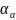(угол давления), а плечо этой силы (высота
зуба) – как
,
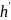то величина момента изгиба
относительно этого основания равна
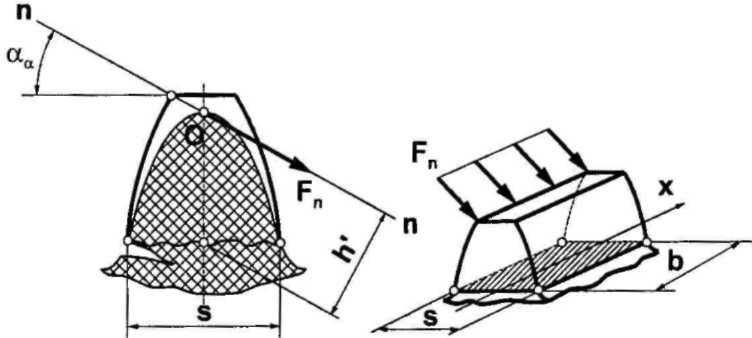
а) б)
Рис. 2.4
Величина
угла давления
принимается равной
.
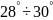Изгибающий момент вызывает появление
напряжений растяжения у основания зуба.
Максимальная величина напряжений
растяжения
(без учета концентраторов) имеет место
на внешней поверхности основания:
где
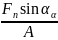– напряжение сжатия, вызванное радиальной
составляющей нормальной силы в опасном
сечении зуба,
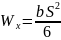– момент сопротивления поперечного
сечения зуба и его основания.
Окончательно для изгибной прочности зубчатого зацепления прямозубыми колесами
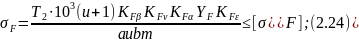
где
– коэффициент формы зуба,
– допускаемое напряжение усталостной прочности на изгиб.
Коэффициент принимается:
для колеса внешнего зацепления
для колеса внутреннего зацепления
где
z
и
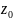– число зубьев колеса и долбяка
соответственно;
x – коэффициент смещения инструмента при нарезании зубчатого колеса.
При
практическом применении для колес
внутреннего зацепления коэффициент
формы зуба приближенно можно принимать
равным
.
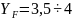Условие
изгибной прочности должно быть выполнено
для каждого из колес зубчатой пары. Если
на прочность рассчитывается колесо, то
в (2.24) подставляют
и
,
а при расчете прочности шестерни -
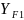и
.
Значение коэффициента учета торцевого
перекрытия рекомендуется считать равным
единице:
.
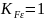Для силовых зубчатых передач основным прочностным расчетом является расчет по контактным напряжениям, в то время как расчет прочности по изгибу выполняется как проверочный, главным образом с целью определения модуля зубчатой передачи. Выражая m из (2.24), имеем
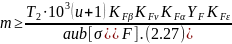
Полученное по формуле (2.27) значение модуля нужно округлить до ближайшего большего значения из стандартного ряда модулей (табл.2.7).
Таблица 2.7. Стандартные значения модулей m зубьев зубчатых колес
1-й ряд |
1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25; 32; 40; 50; 60; 80; 100 |
2-й ряд |
1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14; 18; 22; 28; 36; 45; 55; 70; 90 |
С
формальной точки зрения расчет прочности
косозубого цилиндрического колеса
может быть заменен расчетом прямозубого
с приведенным числом зубьев
.
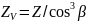Поэтому формулы расчета прочности
прямозубых колес на изгиб можно
использовать и при расчете косозубых.
Однако при записи окончательной расчетной
формулы изгибной прочности следует
помнить, что для косозубого зацепления
характерно осевое перекрытие, которое
существенно повышает нагрузочную
способность колеса. Величина осевого
перекрытия зависит прежде всего от угла
наклона зуба и может быть учтена в
окончательном выражении введением
поправочного коэффициента
.
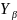Тогда условие прочности косозубой
зубчатой передачи при изгибе записывается
в виде
Исследования показали, что коэффициент учета осевого перекрытия можно приближенно рассчитывать по формуле
где – угол наклона зубьев в градусах.
Что
касается коэффициента формы зуба
,
то при вычислении применительно к
косозубым колесам следует в формулах
(2.25-2.26) заменять число зубьев Z
на приведенное
.
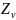