
- •Иркутский государственный технический университет
- •664074, Иркутск, ул. Лермонтова, 83
- •Введение
- •1 Выбор материала зубчатых колес, термической обработки, твёрдости и определение допускаемых напряжений
- •1.1 Материалы зубчатых колес
- •1.2 Термическая и химико-термическая обработка сталей
- •1.3 Наиболее распространенные варианты термической обработки
- •1.4 Внешняя нагрузка и кривая усталости
- •1.5 Определение допускаемых контактных напряжений при постоянном режиме нагружения
- •1.6 Определение допускаемых напряжений изгиба при постоянном режиме нагружения
- •1.7 Определение допускаемых напряжений при переменном режиме нагружения
- •1.8 Типовые режимы нагружения
- •1.9 Последовательность определения допускаемых напряжений
- •1.10 Пример определения допускаемых напряжений
- •2 Проектировочный расчет цилиндрической зубчатой передачи
- •2.1 Силы, действующие в зацеплении цилиндрических зубчатых колес
- •Распределение нагрузки в зубчатых передачах
- •Коэффициент концентрации нагрузки при расчете контактных напряжений
- •Коэффициент концентрации нагрузки при расчете напряжений изгиба
- •Коэффициент динамической нагрузки при расчете контактных напряжений
- •Коэффициент динамической нагрузки при расчете изгибных напряжений
- •(Для многопарного зацепления)
- •Причины разрушения и критерии расчета зубчатых передач
- •Расчет цилиндрических передач на контактную прочность
- •Расчет цилиндрических передач на прочность при изгибе
- •Пример проектировочного расчета цилиндрической косозубой передачи внешнего зацепления
- •Определение величины межосевого расстояния из расчета прочности по контактным напряжениям
- •Определение значения модуля из расчета прочности по напряжениям изгиба
- •Расчет коэффициентов динамичности нагрузки
- •Проверка выполнения условия прочности по контактным напряжениям
- •Проверка выполнения условия прочности по напряжениям изгиба
- •Список литературы
Причины разрушения и критерии расчета зубчатых передач
Наиболее опасной причиной разрушения зубчатых колес является поломка зуба, вызванная изгибом. Этот вид разрушения носит усталостный характер и начинается с зарождения трещины в наиболее напряженной части: у основания зуба в зоне растяжения. Размеры трещины увеличиваются и достигают таких значений, при которых происходит скол части зуба, или излом. Для предотвращения такого вида разрушения зубья колеса рассчитываются на изгибную прочность. Еще одной, самой распространенной, причиной разрушения зубчатых колес является так называемое выкрашивание контактной поверхности зубьев. Этот вид разрушения характерен для передач, работающих в условиях обильной смазки. Он также носит усталостный характер и начинается с образования трещин на контактной поверхности зубьев. Рост такой трещины приводит к отслаиванию локальных участков поверхности, а процесс, приводящий к отслаиванию, и называется выкрашиванием. Для предотвращения выкрашивания проверку контактной прочности передачи.
При проектировании малонагруженных передач, как металлических, так и изготовленных из неметаллических материалов, необходимо учитывать, необходимо учитывать, что основной причиной нарушения их работоспособности является износ. Такое разрушение характерно и для открытых передач, т.е. передач, эксплуатируемых в условиях сильного загрязнения среды, а также для передач, работающих при недостаточной смазке. При этом поверхность зуба истирается, а сам зуб истончается и может разрушиться из-за потери изгибной прочности. Методика расчета износостойкости таких передаточных механизмов до настоящего времени не разработана, поэтому для определения их основных геометрических размеров проводят расчет на изгиб, а скорость износа при этом определяется соответствующим выбором величины допускаемых напряжений изгиба. Очевидно, что износ может повлиять и на другие параметры зубчатого зацепления, такие как потеря точности, повышенный шум, вибрация и т.п.
В отдельных случаях в зубчатых передачах наблюдается явление заедания, при котором имеет место межмолекулярное взаимопроникновение частиц зубьев колеса и шестерни из-за повышенных температур в контакте. Повышение температуры, в свою очередь, может быть вызвано большими скоростями относительного скольжения зубьев.
Расчет цилиндрических передач на контактную прочность
В
Рис. 2.3
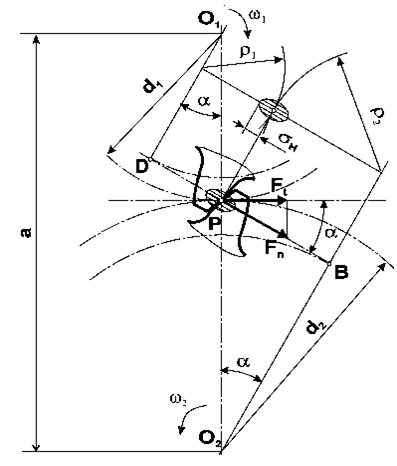 точке соприкосновения зубьев возникают
контактные напряжения, что, в конечном
итоге, и приводит к усталостному
разрушению контактной поверхности
зуба, которое выражается в выкрашивании
этой поверхности. Главным фактором,
влияющим на процесс выкрашивания,
является величина наибольшего напряжения
в точках контакта зубьев.
точке соприкосновения зубьев возникают
контактные напряжения, что, в конечном
итоге, и приводит к усталостному
разрушению контактной поверхности
зуба, которое выражается в выкрашивании
этой поверхности. Главным фактором,
влияющим на процесс выкрашивания,
является величина наибольшего напряжения
в точках контакта зубьев.
Рассмотрим
случай контактного взаимодействия
зубьев в полюсе зацепления, где существует
наибольшая вероятность возникновения
усталостных трещин (рис. 2.3). Максимальное
напряжение
 при линейном касании двух цилиндров по
формуле Герца:
при линейном касании двух цилиндров по
формуле Герца:
где
 – модули упругости, а
– модули упругости, а
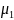 ,
,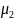 – коэффициенты Пуассона материалов
зубчатых колес;
– коэффициенты Пуассона материалов
зубчатых колес;
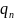 – нормальная нагрузка на единицу длины
контактной линии зуба. Величина 1/
– нормальная нагрузка на единицу длины
контактной линии зуба. Величина 1/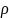 имеет смысл суммарной кривизны
контактирующих цилиндров:
имеет смысл суммарной кривизны
контактирующих цилиндров:
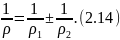
Знак «–» соответствует случаю внутреннего зацепления.
Окончательное выражение для расчета максимальных нормальных напряжений в контакте зубьев зубчатых колес:
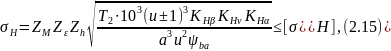
где
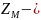 постоянная, зависящая от параметров
материалов колес
постоянная, зависящая от параметров
материалов колес
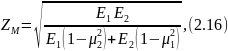
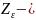 коэффициент,
являющийся функцией величины торцевого
перекрытия
коэффициент,
являющийся функцией величины торцевого
перекрытия
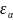 :
для косозубых колес
:
для косозубых колес
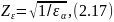
для прямозубых колес
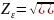
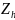 -
параметр геометрии зацепления:
-
параметр геометрии зацепления:
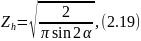
где
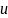 – передаточное отношение,
– передаточное отношение,
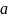 – межосевое расстояние;
– межосевое расстояние;
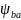 – коэффициент ширины колеса,
– допускаемое контактное напряжение.
– коэффициент ширины колеса,
– допускаемое контактное напряжение.
Коэффициент
ширины колеса b
к межосевому расстоянию
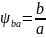 выбирается
в зависимости от расположения шестерни
относительно опор:
выбирается
в зависимости от расположения шестерни
относительно опор:
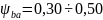 – симметричном;
– симметричном;
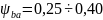 – асимметричном;
– асимметричном;
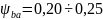 – консольном;
– консольном;
а
для передач шевронными колесами
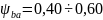 .
.
Выбор допускаемого контактного напряжения зависит от материала колес, их термообработки, твердости поверхности зубьев и т.д.
При
проведении проектировочного расчета
стальных зубчатых колес принимаем
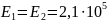 МПа,
МПа,
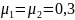 .
Угол зацепления примем равным
.
Угол зацепления примем равным
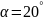 ,
а коэффициент учета перекрытия
,
а коэффициент учета перекрытия
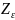 =
1,0 для прямозубых колес и
= 0,9 для косозубых колес. Тогда, выражая
межосевое расстояние
из условия прочности (2.15) и используя
усредненные значения константы материала
=
1,0 для прямозубых колес и
= 0,9 для косозубых колес. Тогда, выражая
межосевое расстояние
из условия прочности (2.15) и используя
усредненные значения константы материала
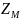 (2.16), коэффициент перекрытия
(2.17-2.18) и параметра зацепления
(2.16), коэффициент перекрытия
(2.17-2.18) и параметра зацепления
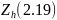 ,
для контакта прямозубых колес имеем
,
для контакта прямозубых колес имеем
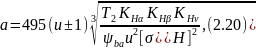
а для зацепления косозубыми зубчатыми колесами –
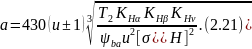
Знак «–» в (2.20-2.21), как обычно, относится к случаю внутреннего зацепления колес.
Полученное по формуле (2.21) значение межосевого расстояния нужно округлить до ближайшего большего значения из стандартного ряда (табл.2.6)
Таблица 2.6. Стандартные значения межосевых расстояний
1-й ряд |
40; 50; 63; 80; 100; 125; 160; 200; 250; 315; 400; 500; 630; 800; 1000; 1250; 1600; 2000; 2500 |
2-й ряд |
71; 90; 112; 140; 180; 224; 280; 355; 450; 560; 710; 900; 1120; 1400; 1800; 2240 |
