3. Алгоритм решения задач на составление дифференциальных уравнений

На основании рассмотренных ранее задач на составление дифференциальных уравнений получаем алгоритм решения таких задач:

1⁰. Из переменных величин выделяют функцию и аргумент, устанавливают физический смысл функции и ее произ­водной. Затем, используя известные сведения из физики, механики, электротехники и других дисциплин, выражают зависимость между функцией, ее производной и аргумен­том, т. е. составляют дифференциальное уравнение.

2°. Определяют, к какому типу относится составленное урав­нение и находят его общее решение.

3⁰. Если в задаче даны начальные условия, то получают част­ное решение уравнения.

408

4. Дополнительные задачи на составление дифференциальных уравнений

Перед рассмотрением решений задач данного раздела следует еще раз просмотреть решения задач п. 3 § 1 и п. 4 § 2.

192. Металлический шар, температура которого в начале опыта была равна 12 °С, охлаждается струей воды, имеющей температуру 0°. Через 8 мин шар охладился до 9⁰. Считая ско­рость охлаждения пропорциональной разности между темпера­турой тела и температурой охлаждающей среды, определить, в течение какого времени шар охладился до 7°.

Возведя в степень t обе части этого равенства, имеем

409

Чтобы ответить на вопрос задачи, прологарифмируем по основа­нию 10 равенство (2):

и положим в полученном равенстве 7⁰= 7:

Отсюда окончательно находим

193. Сосуд вместимостью 100 л наполнен рассолом, содержа­щим 10 кг растворенной соли. За 1 мин в него втекает Зл воды и столько же смеси перекачивается в другой сосуд той же вмести­мости, первоначально наполненный водой, из которого избыток жидкости выливается. В какой момент времени количество соли в обоих сосудах окажется одинаковым?

410

общий интеграл которого имеет вид

Значение постоянной С₂ определяем из начальных условий; так как y=0 при t= 0, то С₂ = 0. Следовательно, зависимость количества соли у во втором сосуде от времени t выражается равенством

Искомый момент времени, в который количество соли в обоих сосу­дах станет одинаковым, найдем, полагая х = у:

В этот момент в каждом сосуде окажется по 10/е * 3,68 кг соли.

194. Конденсатор емкостью Q включается в цепь с напряже­нием U и сопротивлением R. Определить заряд q конденсатора в момент t после включения.

411

где знак минус показывает, что сила сопротивления направлена в сто­рону, противоположную движению.

Разделим переменные и проинтегрируем:

412

В скобках записано развернутое выражение синуса суммы двух углов и а. В результате получим соотношение

выражающее закон простого гармонического колебательного движения.

197. Гиря, поддерживаемая спиральной пружиной, приподнята на расстояние b и затем освобождена. Она начинает падать, причем ее ускорение определяется уравнением , где р — постоянная, as— расстояние от положения равновесия.

Найти уравнение движения.

Для определения произвольных постоянных Л и б воспользуемся начальными условиями. При t=0 имеем s = b; следовательно,

Найдем скорость в данный момент:

и воспользуемся тем, что v = 0 при t = О. Имеем

так как , то А = 0.

Итак, уравнение движения имеет вид s = bcos pt. Функции cos pt — периодическая, поэтому и s является периодической функцией; функ­ция s будет периодически то возрастать, то убывать, т. е. гиря будет совершать колебательное движение то вниз, то вверх.

198. К источнику с э.д.с, равной e(t), подключают контур, состоящий из последовательно соединенных катушки, индуктив­ности L, омического сопротивления R и емкости С (рис.206). Найти силу тока i в цепи как функцию времени t, если в начальный момент времени сила тока в контуре и заряд конденсатора равны нулю.

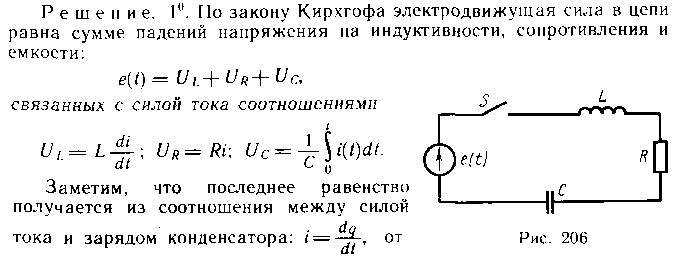
413

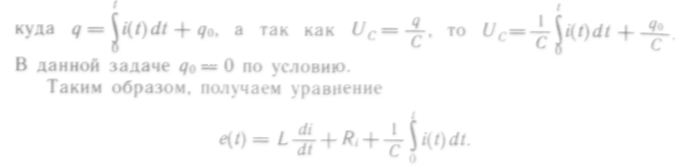
2⁰. Это уравнение — интегрально-дифференциальное. Продифферен­цировав его по t, получим линейное дифференциальное уравнение вто­рого порядка с постоянными коэффициентами:

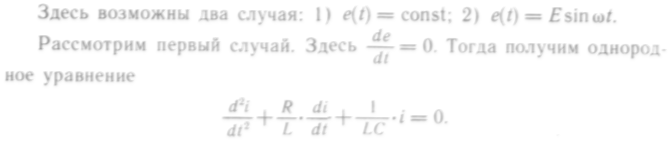
Характеристическое уравнение

имеет корни

414

Итак, частное решение уравнения принимает вид

Замечание. При рассмотрении второго случая получается линейное неоднородное уравнение второго порядка с постоянными коэффициентами

которое в данном пособии не рассматривается.

Вопросы и задачи для конспектирования

415

45. Тело, температура которого 25⁰С, погружено в термостат, в котором поддерживается температура 0⁰С. Зная, что скорость охлаждения тела про­порциональна разности между температурами тела и окружающей среди, опре­делите, за какое время тело охладится до 10°С, если за 20 мин оно охлаждается до 20⁰С.

416

Ответы