5. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Прежде чем дать определение нового вида дифференциаль­ного уравнения, раскроем подробно его название:

398

1) дифференциальное уравнение (по определению) обязательно содержит производные или дифференциалы искомой функции;

2) уравнение второго порядка содержит производную, наивысший порядок которой равен 2;

3. это уравнение — линейное относительно искомой функции и ее производных, т. е. содержит их в первой степени;

4. это — уравнение с постоянными коэффициентами; значит, коэффициенты при функции и ее производных являются постоян­ными величинами.

Учитывая все это, можно сказать, что рассматриваемое урав­нение содержит у, у', у" в первой степени и коэффициенты при них — постоянные величины.

Коэффициент при у" всегда можно сделать равным единице, полученные при этом коэффициенты при у¹ и у обозначим через р и q. Тогда получим уравнение вида

где р и q — постоянные величины, a f(x) — непрерывная функ­ция х.

Если правая часть уравнения (4) равна нулю, т. е.

то оно называется уравнением без правой части (или однород­ным уравнением).

Напомним, что общее решение дифференциального уравне­ния второго порядка содержит две произвольные постоянные.

Для нахождения общего решения этого уравнения рассмот­рим следующие теоремы.

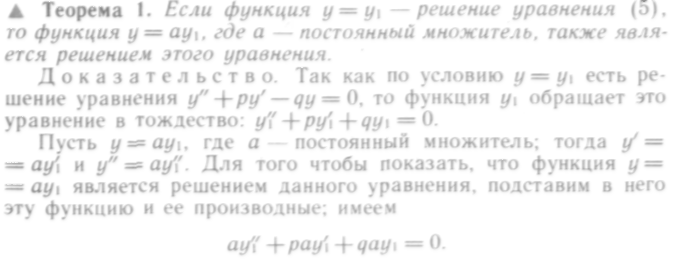
399

Вынося а за скобки, получим

Выражение в скобках равно нулю, так как по условию y₁ — решение уравнения.

Очевидно, что функция ау₁ обращает данное уравнение в тождество, т. е. является его решением, что и требовалось дока­зать.

Раскрыв скобки и перегруппировав члены уравнения, по - лучим

400

Известно, что при решении квадратного уравнения могут получиться корни следующих видов: 1) действительные и раз­личные; 2) действительные b разные; 3) комплексные.

Каждому виду корней квадратного уравнения соответствует свой вид решения дифференциального уравнения.

I с л у ч а й. Корни к₁ и k₂-действительные и различные

401

Далее, находим

Подставляем начальные данные:

402

т.е. получили тождество. Следовательно, у₂= хе^2x — второе частное решение. Эти два решения линейно независимы. Поэтому общее реше­ние записывается в виде

Обычно их преобразуют так, чтобы избавиться от мнимых величин в показателе степени. Для этого используют формулы Эйлера:

(эти формулы мы принимаем без доказательства). Отсюда

Общее решение имеет вид

Группируя члены и обозначая С₁ = С_I+С_II и C₂ = (C_I — C_II)i, получим

403

На основании рассмотренных примеров получаем алгоритм решения линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами.

404

Для практического использования указанный алгоритм удоб­но оформить в виде следующей таблицы:

156—179. Найти общие решения уравнений:

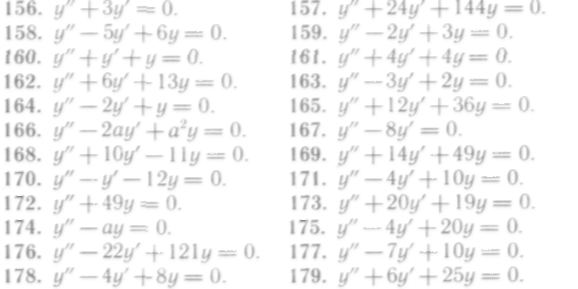
180 — 188. Найти частные решения уравнений, удовлетворяющие заданным начальным условиям:

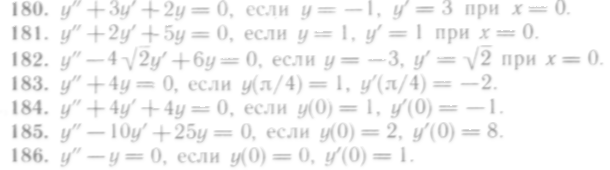
405

Как было отмечено ранее, геометрически общее решение дифференциального уравнения представляет собой семейство интегральных кривых. Геометрический смысл частного решения состоит в нахождении интегральной кривой, проходящей через данную точку.

Чтобы найти уравнение искомой интегральной кривой, подставим в равенства