§ 4. Дифференциальные уравнения высших порядков

• 1. Понятие о дифференциальном уравнении высшего порядка

• 2. Дифференциальное уравнение второго порядка и его общее решение

• 3. Задача Коши для простейшего дифференциального уравнении второго порядка

• 4. Задачи, сводящиеся к простейшим дифференциальным уравнениям второго порядка

• 5. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

393

1. Понятие о дифференциальном уравнении высшего порядка

Как было отмечено выше, дифференциальные уравнения при­нято классифицировать в зависимости от порядка производной, входящей в уравнение.

Дифференциальное уравнение n-го порядка имеет вид

(напомним, что символом y⁽ⁿ⁾ обозначается производная п-го порядка).

Если же уравнение (1) можно разрешить относительно стар­шей производной (т. е. относительно y⁽ⁿ⁾), то оно примет вид

Общим решением уравнения п-го порядка называется семей­ство функций , которое при любом наборе произвольных постоянных С₁, С₂, ..., С_п удовлетворяет исходному уравнению.

Общее решение дифференциального уравнения должно со­держать столько произвольных постоянных, каков порядок этого уравнения; так, если уравнение имеет первый порядок, то оно должно содержать одну произвольную постоянную. Ниже будут рассмотрены некоторые дифференциальные уравнения второго порядка, общие решения которых содержат две произвольные постоянные.

Частным решением дифференциального уравнения п-го по­рядка называется функция , получающаяся при подста­новке некоторого набора произвольных постоянных С₁, С₂, ..., С_п в общее решение этого уравнения.

2. Дифференциальное уравнение второго порядка и его общее решение

Уравнение, содержащее производные или дифференциалы второго порядка, называется дифференциальным уравнением второго порядка.

Дифференциальное уравнение второго порядка, разрешенное относительно у", имеет вид

Простейшим дифференциальным уравнением второго порядка является уравнение вида

Такое уравнение решается двукратным интегрированием:

394

откуда

Проинтегрировав эту функцию, получим какую-то новую функ­цию от f(x), которую обозначим через F(x). Таким образом.

Интегрируем еще раз:

или

Итак, получили общее решение данного дифференциального уравнения, содержащее две произвольные постоянные С₁ и С₂.

110. Найти общее решение уравнения у" = 4х.

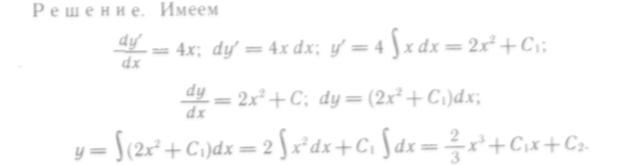
Полученный результат проверим дифференцированием:

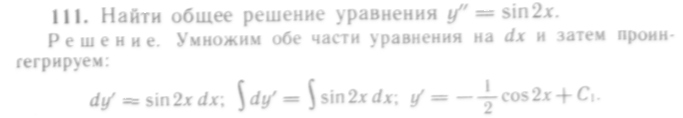
Обе части последнего уравнения умножим на dx и проинтегри­руем:

112—119. Найти общие решения уравнений:

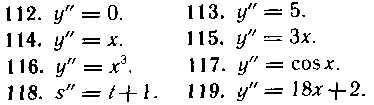
395

В общее решение уравнения первого порядка входит одна произвольная постоянная С, а в общее решение уравнения вто­р ого порядка — две произвольные постоянные С₁ и C₂.

3. Задача Коши для простейшего дифференциального уравнения второго порядка

Задача Коши для дифференциального уравнения второго порядка состоит в том, чтобы найти решение, удовлетворяющее начальным условиям.

396

4. Задачи, сводящиеся к простейшим дифференциальным уравнениям второго порядка

В задачах, решение которых приводит к интегрированию диф­ференциальных уравнений, используют известные законы физики, механики и других наук.

При решении задач сначала нужно составить дифферен­циальное уравнение по условию задачи, а затем найти решение этого уравнения по общему правилу.

Интегрируем еще раз:

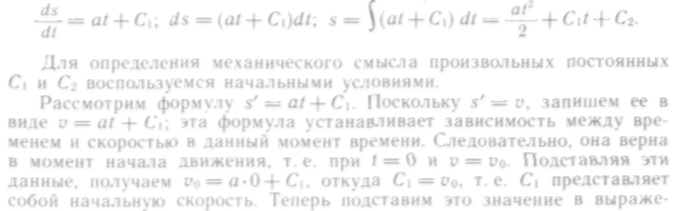
397

Итак,

Это и есть общее уравнение движения тела с постоянной скоростью.

Если s = 0 и v_о = 0, то последняя формула принимает вил

и называется формулой пути при равнопеременном движении.