§ 3. Линейные дифференциальные уравнения первого порядка

• 1. Основные понятия

• 2. Решение линейных дифференциальных уравнений первого порядка методом Бернулли

• 3. Задача Коши для линейного дифференциального уравнения первого порядка

• 4. Линейные дифференциальные уравнения вида у' +ау = b и у^/= ау.

• 5. Линейное дифференциальное уравнение первою порядка с искомой функцией х(у)

1. Основные понятия

13-1356 385

79. Являются ли линейными дифференциальными уравнения­ми первого порядка следующие уравнения:

Линейное уравнение может быть одновременно и уравнением с разделяющимися переменными, например _. В этом случае оно решается как уравнение с разделяющимися перемен­ными.

К уравнениям с разделяющимися переменными относятся линейные уравнения первого порядка без правой части (т. е. при q= 0). Например, линейные уравнения

могут быть решены сразу разделением переменных и интегриро­ванием.

2. Решение линейных дифференциальных уравнений первого порядка методом Бернулли

где и и v — новые функции переменной х.

Одну из этих функций подбирают так, чтобы уравнение, со­держащее другую функцию, стало уравнением с разделяющими­ся переменными.

Рассмотрим решение линейных дифференциальных уравне­ний первого порядка на примерах.

386

Считая, что неизвестная функция у является произведением двух (также неизвестных) функций и и v мы тем самым можем одну из этих функций выбрать произвольно. Поэтому приравняем нулю коэффи­циент при и в уравнении (1):

Разделяя переменные в полученном уравнении, имеем

Снова ввиду произвольности в выборе v мы можем не учитывать произ­вольную постоянную С (точнее — можем приравнять ее нулю). Найденное значение v подставляем в уравнение (1):

(здесь С писать обязательно, иначе получится не общее, а частное решение).

или

Из двух функций и и v одну можно выбрать произвольно; поэтому определим функцию v так, чтобы множитель при и в уравнении (2) обратился в нуль, т. е. чтобы

откуда

(произвольную постоянную С принимаем равной нулю).

13* 387

Подставляя выражение функции v в уравнение (2), для определе­ния и получаем уравнение

откуда

Так как , то общее решение заданного уравнения примет вид

Из рассмотренных примеров легко установить алгоритм ре­шения линейного дифференциального уравнения первого по­рядка.

388

3. Задача Коши для линейного дифференциального уравнения первого порядка

Выберем v так, чтобы

откуда

Подставив выражение v в уравнение (4), для определения и полу­чаем уравнение

389

откуда

Поскольку y=uv, общее решение заданного уравнения записы­вается в виде

94—101. Найти частные решения уравнений, удовлетворяющие указанным начальным условиям:

390

Полученное уравнение является дифференциальным уравнением показательного роста; его общее решение имеет вид

Итак, скорость движения катера после выключения двигателя определяется формулой

391

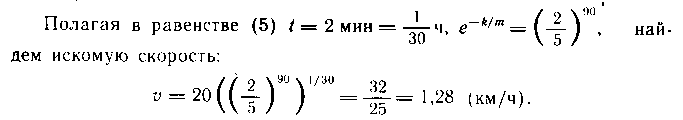
5. Линейное дифференциальное уравнение первого порядка с искомой функцией х(у)

Иногда уравнение становится линейным, если у считать не­зависимой переменной, ах — зависимой, т. е. поменять роли л и у. Это можно сделать при условии, что х и dx входят в урав­нение линейно.

Разделив обе части последнего уравнения на произведение y dy, при­ведем его к виду

392

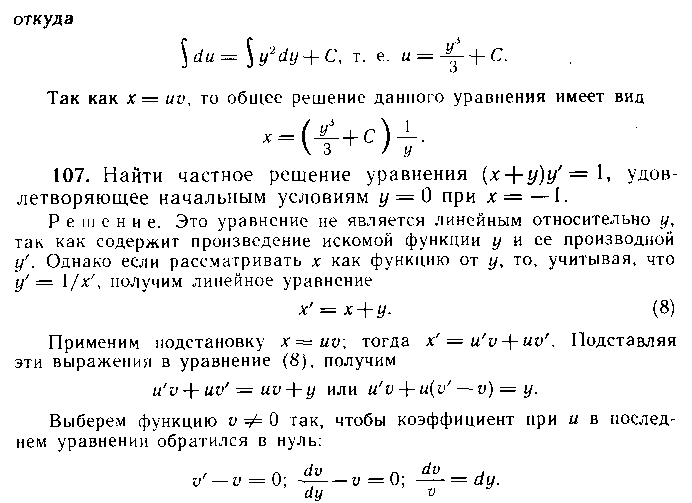
Интегрируя, имеем

Далее, находим

Таким образом, общее решение уравнения есть