2. Условная вероятность

При совместном рассмотрении двух случайных событий А и В часто возникает вопрос: как связаны события А и В друг с другом, как наступление одного из них влияет на возможность наступления другого?

Простейшим примером связи между двумя событиями служит причинная связь, когда наступление одного из событий обязательно приводит к наступлению другого, или наоборот, когда наступление одного исключает возможность наступления другого. Пусть, например, из ящика наугад выбрана деталь и собы­тие А заключается в том, что эта деталь стандартна (не содер­жит брака), а событие В состоит в том, что эта деталь 1-го сорта. Тогда наступление события B (1-го сорта) влечет за собой наступление события А (деталь стандартная). Рассмотрим

430

событие С деталь не принял ОТК. В этом случае наступление события С исключает наступление события А. Однако кроме таких крайних случаев, существует и много промежуточных, когда непосредственная причинная зависимость одного события от другого отсутствует, но искомая зависимость все же имеется.

В повышает вероятность события А.

Для характеристики зависимости одних событий от других вводится понятие условной вероятности.

62. В ящике находятся 10 лампочек по 15 Вт, 10- по 25 Вт, 15 по 60 Вт и 25 по 100 Вт. Определить вероятность того, что взятая наугад лампочка имеет мощность более 60 Вт, если известно, что число ватт на взятой лампочке четное.

431

63. На игральной кости грани 1, 2, 3 окрашены в красный цвет, а грани 4, 5, 6 в черный. При бросании кости выдала черная грань. Какова вероятность тою, что на этой грани стоит четное число?

64. Какова вероятность того, что вытащенная наугад кость домино окажется «дублем», если известно, что сумма очков на этой кости является четным числом ?

Из формулы (3) следует, что

т. е. вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое событие произошло.

Полученная формула имеет смысл, если существуют вероят­ности событий , т. е. если события А и В сов­местны.

3. Независимость событий. Теорема умножения вероятностей

Событие А называется независимым от события В, если на­ступление события В не оказывает никакого влияния на вероят­ность наступления события А.

Теорема 2 (теорема умножения вероятнос­тей). Вероятность одновременного появления двух независимых событий равна произведению вероятностей этих событий.

432

Чаще всего для определения независимости событий поль­зуются интуицией; так, например, при бросании двух монет оче­видно, что выпадение какой-либо стороны на одной из них не оказывает влияния на условия бросания другой и, следователь­но, выпадения каких-либо сторон на каждой из них представля­ют собой независимые события.

Понятие независимости обобщается на любое число событий.

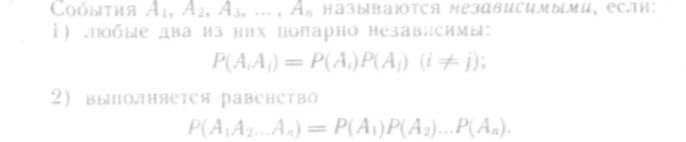
65. В гарной урне находятся 6 черных и 4 белых шара, во второй 5 черных и 7 белых шаров. Из каждой урны извлекают по одному шару. Какова вероятность того, что оба шара окажутся белыми?

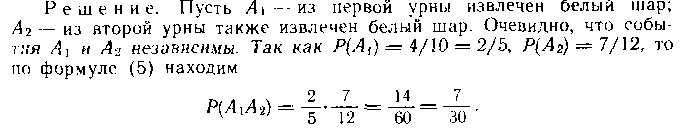
66. Прибор состоит из двух элементов, работающих незави­симо. Вероятность выхода из строя первого элемента равна 0,2; вероятность выхода из строя второго элемента равна 0,3. Найти вероятность того, что: а) оба элемента выйдут из строя; б) элемента будут работам.

Тогда событие, состоящее в том, что будут работать оба элемента, есть и. значит,

67. В экзаменационные билеты включено по два теоретических вопроса и по одной задаче. Всего составлено 28 билетов. Вычислить вероятность тою. что. вынув наудачу билет, учащий­ся ответит на все вопросы, если он подготовил 50 теоретических вопросов и 22 задачи.

433

Решение. Полный ответ на билет состоит из произведения двух событий: учащийся одновременно ответит на два вопроса (событие А) и решит задачу (событие В). Вычистим вероятности этих событий.

Число всех возможных комбинаций из 56 вопросов но два составляет

Так как учащийся подготовил только 50 вопросов, то число исходов, благоприятствующих событию A, есть,

Вычислим вероятность события А:

Вероятность события В определяется тем, что учащийся знает 22 за­дачи из 28 возможных:

Поскольку события А и В независимы и должны выполняться одно­временно, имеем

68. Вероятность сдачи зачета учащимся равна 0,8, а вероят­ность сдачи экзамена равна 0,9. Какова вероятность того, что учащийся сдаст экзамен?

69. Игральную кость бросают трижды. Какова вероятность того, что цифра 5 выпадет три раза?

70. Игральную кость бросают трижды. Какова вероятность того, что ни разу не выпадет цифра 6?

71. Электрическая схема состоит из пяти последовательно со­единенных блоков. Вероятности безотказной работы каждого бло­ка составляют 0,3; 0,5; 0,8; 0,1; 0,2. Считая выходы из строя раз­личных блоков независимыми событиями, найти надежность всей схемы в целом.

72. Электрическая схема состоит из трех параллельно соеди­ненных блоков. Вероятности безотказной работы каждого блока составляют 0,3; 0,7; 0,85. Считая выходы из строя различных бло­ков независимыми событиями, найти надежность всей схемы в целом.

73. Имеется две урны. В первой урне находятся 1 белый, 3 чер­ных и 4 красных шара; во второй — 3 белых, 2 черных и 3 красных тара. Из каждой урны достают по одному шару и сравнивают их цвета. Найти вероятность того, что цвета обоих шаров совпа-

434