§ 3. Операции над событиями

• 1. Теорема сложении вероятностей

• 2. Условная вероятность

• 3. Независимые события. Теорема умножения вероятностей

• 4. Формула полной вероятности

1. Теорема сложения вероятностей

После рассмотрения этого примера можно сформулировать следующую теорему.

Теорема 1 (теорема сложения вероятностей). Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.

Доказательство. Пусть в результате опыта могут наступить п несовместных исходов, которые по соображениям

427

симметрии будем считать равновероятными. Далее, пусть т_а — число равновозможных исходов, благоприятствующих событию А; т_ь — число равновозможных исходов, благоприятствующих событию В.

Так как события А и В несовместны, то не существует таких исходов, которые одновременно благоприятствовали бы и А, и В. Поэтому событию благоприятствуют исходов.

Доказанную теорему с помощью метода математической индукции можно распространить на случай нахождения вероят­ности суммы попарно несовместных событии :

Следствие 1. Если события А, В,…, М образуют пол­ную систему, то сумма вероятностей этих событий равна еди­нице.

Действительно, по теореме о вероятности суммы несовместных событий имеем . Так как эти события образуют полную систему, то их сумма представляет собой достоверное событие (т. е. наступит хотя бы одно из них); но вероятность достоверного события равна 1, т.е. .

Следствие 2. Сумма вероятностей противоположных событий А и А равна единице.

Вероятность события, противоположного событию А, равна разности между единицей и вероятностью события ,4, т.е.

Действительно, события Л и Л образуют полную систему, а потому на основании следствия 2 можем записать:

откуда

49. Имеется 100 лотерейных билетов. Известно, что на 5 биле­тов попадает выигрыш по 20 руб., на 10 — по 15 руб., на 15 —по 10 руб., на 25 — по 2 руб. и на остальные — ничего. Найти вероятность того, что на купленный билет будет получен выигрыш не меньше 10 руб.

Решение. Пусть А, В и С события, состоящие в том, что на купленный билет падает выигрыш, равный соответственно 20, 15 и 10 руб. Так как события А, В и С несовместны, то

50. В корзине находятся 5 белых и 7 черных перчаток. Найти вероятность того, что пара, которую достали наугад, окажется одноцветной.

428

51. В коробке находятся 250 лампочек, из них 100 по 100 Вт, 50 — по 60 Вт, 50 — по 25 Вт и 50 — по 15 Вт. Вычислить вероятность того, что мощность любой взятой наугад лампочки не превысит 60 Вт.

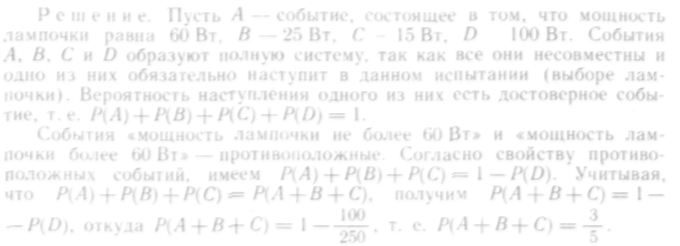
52. Из урны, содержащей белые, черные и синие шары, из­влекают один шар. События 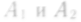означают появление соответ­ственно белого и черного шаров. Что означает событие ?

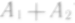53. Дана электрическая пень с элементами , соединенными последовательно. Событие А — выход из строя элемента Л; событие В выход из строя элемента l₁. Что означает собы­тие А+В?

54. Событие А означает появление шести очков на верхней грани игрального кубика. Что означает событие А?

55. Событие А состоит в том, что хотя бы одна из 15 имею­щихся электрических лампочек нестандартная. Что означает со­бытие

56. В группе 5 человек учится на отлично, 7 человек—на хороню и отлично, 15 человек имеют тройки и 3 человека — неудовлетворительные оценки. Определи и, вероятность того, что вызванный учащийся не имеет ни двоек, ни троек.

57. У продавца имеется 10 красных, 8 синих, 5 зеленых и 15 желтых шаров. Вычислить вероятность того, что купленный шар окажется красным, синим или зеленым.

Произведением конечного числа событие называется событие, состоящее в том. что каждое из них произойдет.

П усть А и В — произвольные события. Далее, пусть т - число равновозможных исходов, благоприятствующих событию

429

т. е.

Полученная формула представляет собой обобщение формулы вероятности суммы двух несовместных событий, поскольку если А и В несовместны, то и формула (2) примет вид (1).

Равенство (2) означает, что вероятность суммы двух совмест­ных событий равна сумме вероятностей этих событий минус ве­роятность произведения этих событий.

58. Из 30 учащихся спортивной школы 12 человек занимают­ся баскетболом, 15—волейболом, 5—волейболом и баскетбо­лом, а остальные — другими вилами спорта. Какова вероятность того, что наудачу выбранный спортсмен занимается только во­лейболом или только баскетболом?