§ 7. Основные свойства и вычисление определенного интеграла

• 1. Простейшие свойства определенного интеграла

• 2. Подстановка в определенном интеграле

• 3. Вычисление определенных интегралов

1. Простейшие свойства определенного интеграла

Рассмотрим основные свойства определенного интеграла. При этом будем предполагать, что функция непрерывна на отрезке [a, b].

1. При перестановке пределов интегрирования знак интеграла меняется на противоположный:

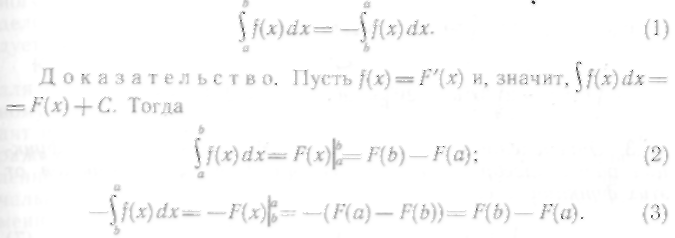
Правые части равенств (2) и (3) равны; следовательно, должны быть равны и левые части, т. е. справедливо соотноше­ние (1).

Это свойство позволяет рассматривать интегралы, в которых верхний предел меньше нижнего.

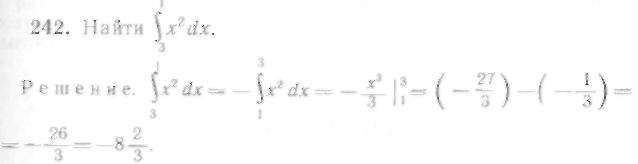
2. Постоянный множитель можно вынести за знак опреде­ленного интеграла, т. е.

где k — постоянная величина.

325

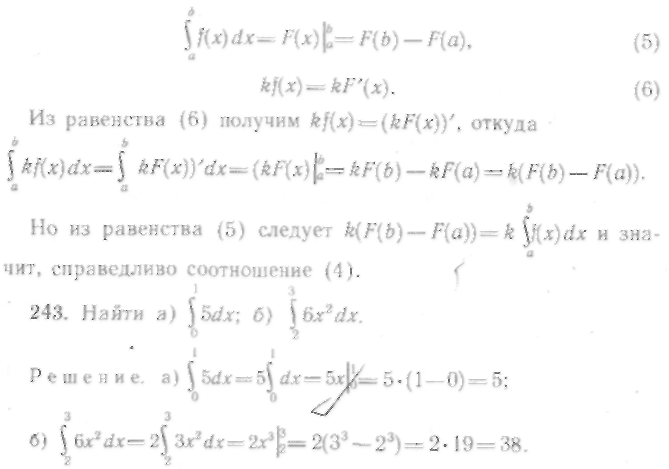
3. Определенный интеграл от алгебраической суммы функ­ций равен алгебраической сумме определенных интегралов от этих функций, т. е.

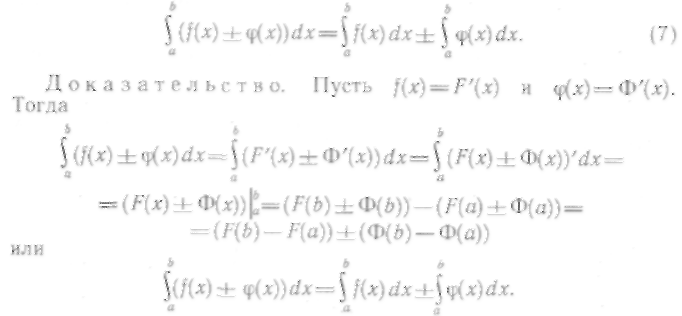
Аналогично можно доказать справедливость этого свойства для любого конечного числа слагаемых.

326

4. Если а, b, с принадлежат интервалу, на котором функция непрерывна, то

Доказательство. Пусть —первообразная функ-

ция для . Тогда

2. Подстановка в определенном интеграле

Для вычисления определенного интеграла с помощью подста­новки поступают так же, как и при вычислении неопределен­ного интеграла этим способом (см. § 5). Однако в случае опре­деленного интеграла имеется одна особенность, на которую сле­дует обратить внимание.

Как мы отмечали, метод подстановки заключается в том, что для приведения заданного неопределенного интеграла к таблич­ному выражают аргумент через новую переменную, а затем нахо­дят неопределенный интеграл и полученный результат снова вы­ражают через первоначальную переменную. В случае же опреде­ленного интеграла нет необходимости возвращаться к первона­чальной переменной, однако нужно помнить, что, заменяя пере­менную под знаком интеграла, следует изменить и пределы интегрирования.

3. Вычисление определенных интегралов

246—306. Вычислить определенные интегралы, используя опре­деление, их свойства и метод подстановки:

327

328

329

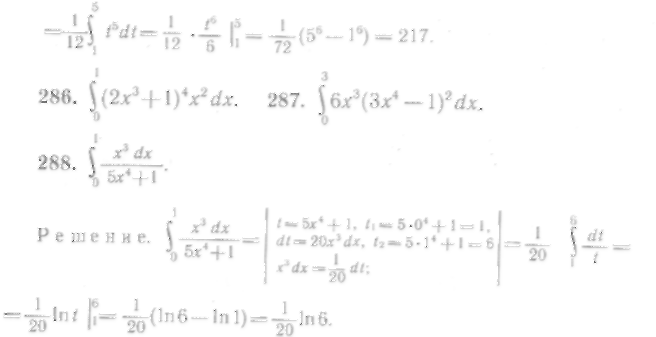
Теперь вычислим этот интеграл иначе, а именно, найдем перво­образную функцию и возвратимся к старой переменной, не меняя пре­делов интегрирования:

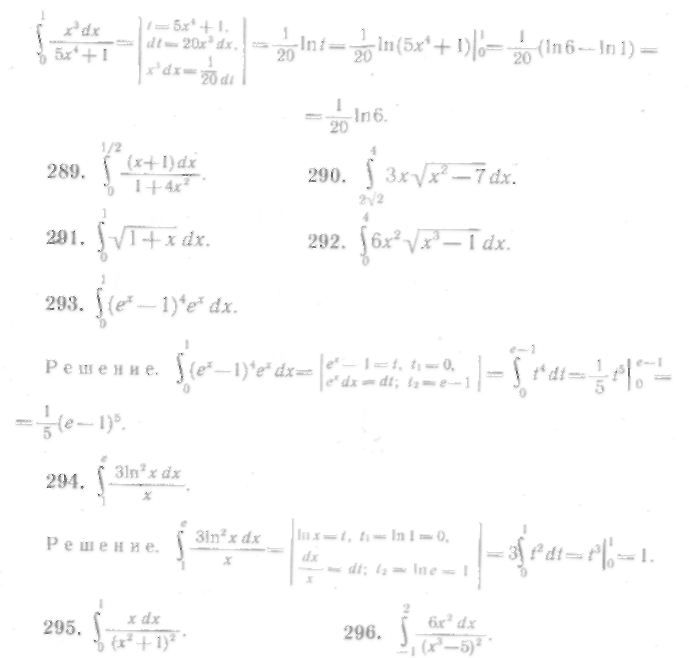
330

§ 8. Вычисление площадей фигур с помощью определенного интеграла

9 1. Правило вычисления площадей плоских фигур

• 2. Площади фигур, расположенных над осью Ох

• 3. Площади фигур, расположенных полностью или частично под

осью Ох

• 4. Площади фигур, прилегающих к оси Оу

• 5. Симметрично расположенные плоские фигуры

1. Правило вычисления площадей плоских фигур

Как известно, определенный интеграл от непрерывной неотри­цательной функции равен площади соответствующей криволи­нейной трапеции (геометрический смысл определенного интег­рала):

331

С помощью определенного интеграла можно также вычислять площади плоских фигур, так как эта задача всегда сводится к вычислению площадей криволинейных трапеций.

Площадь всякой плоской фигуры в прямоугольной системе координат может быть составлена из площадей криволинейных трапеций, прилегающих к оси Ох или к оси Оу.

З адачи на вычисление площадей плоских фигур удобно решать по следующему плану: