
- •Глава V Интеграл и его приложения
- •§ 1. Первообразная
- •1. Дифференцирование и интегрирование — взаимно обратные действия
- •2. Определение первообразной
- •3. Неоднозначность нахождения первообразной
- •§ 2. Неопределенный интеграл и его свойства
- •1. Определение интеграла
- •2. Основные свойства неопределенного интеграла
- •§ 3. Основные табличные интегралы
- •2. Интегрирование по формуле I
- •3. Интегрирование по формуле II
- •4. Интегрирование по формулам III и IV
- •5. Интегрирование по формулам V и VI
- •6. Интегрирование по формулам VII и VIII
- •7. Интегрирование по формулам IX и X
- •§ 4. Приложения неопределенного интеграла
- •2. Выделение из семейства кривых с одинаковым наклоном линии, проходящей через конкретную точку
- •3. Составление уравнения движения тела по заданному уравнению скорости или ускорения его движения
- •§5. Интегрирование подстановкой и по частям
- •1. Способ подстановки (замены переменной)
- •2. Примеры интегрирования подстановкой
- •3. Способ интегрирования по частям
- •§ 6. Определенный интеграл и его геометрический смысл
- •1. Криволинейная трапеция и ее площадь
- •2. Вычисление площади криволинейной трапеции
- •§ 7. Основные свойства и вычисление определенного интеграла
- •1. Простейшие свойства определенного интеграла
- •2. Подстановка в определенном интеграле
- •3. Вычисление определенных интегралов
- •§ 8. Вычисление площадей фигур с помощью определенного интеграла
- •1. Правило вычисления площадей плоских фигур
- •2. Площади фигур, расположенных над осью Ох
- •3. Площади фигур, расположенных полностью или частично под осью Ох
- •4. Площади фигур, прилегающих к оси Оу
- •5. Симметрично расположенные плоские фигуры
- •§ 9. Приближенное вычисление определенного интеграла
- •2. Определенный интеграл как предел суммы
- •3. Метод прямоугольников
- •4. Метод трапеций
- •§ 10. Применение определенного интеграла к решению физических задач
- •1. Схема решения задач на приложения определенного интеграла
- •2. Нахождение пути, пройденного телом при прямолинейном движении
- •3. Вычисление работы силы, произведенной при прямолинейном движении тела
- •4. Вычисление работы, затраченной на растяжение или сжатие пружины
- •5. Определение силы давления жидкости на вертикально расположенную пластинку
- •Контрольное задание
1. Криволинейная трапеция и ее площадь
![]()
Определение 1.
Криволинейной
трапецией называется
фигура, ограниченная графиком
непрерывной неотрицательной
функции
![]() ,
прямыми
,
прямыми
![]() и отрезком
оси Ох. Как
вычислить площадь криволинейной
трапеции? Рассмотрим криволинейную
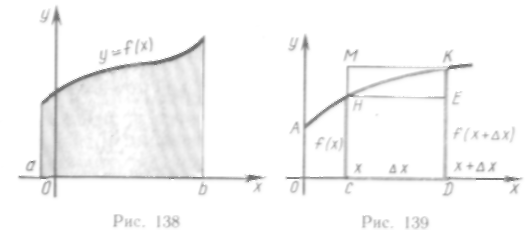
трапецию CHKD
(рис.
139), у которой абсцисса точки С
равна х,
а абсцисса
точки D
равна х+
и отрезком
оси Ох. Как
вычислить площадь криволинейной
трапеции? Рассмотрим криволинейную
трапецию CHKD
(рис.
139), у которой абсцисса точки С
равна х,
а абсцисса
точки D
равна х+![]() х.
Пусть график
функции f(x)
пересекает
ось ординат в точке А.
Тогда площадь
криволинейной трапеции CHKD
равна разности
площадей криволинейных трапеций
OAKD
и ОАНС.
Так как
площадь криволинейной трапеции ОАНС
зависит от
х, то
ее можно обозначить символом
х.
Пусть график
функции f(x)
пересекает
ось ординат в точке А.
Тогда площадь
криволинейной трапеции CHKD
равна разности
площадей криволинейных трапеций
OAKD
и ОАНС.
Так как
площадь криволинейной трапеции ОАНС
зависит от
х, то
ее можно обозначить символом
![]() .
Аналогично, площадь криволинейной
трапеции OAKD
есть функция
от
.
Аналогично, площадь криволинейной
трапеции OAKD
есть функция
от
![]() и ее можно
обозначить символом
и ее можно
обозначить символом
![]() .
Поэтому площадь криволинейной трапеции
CHKD
равна разности
.
Поэтому площадь криволинейной трапеции
CHKD
равна разности
![]() и
и
![]() и может
быть обозначена символом
и может
быть обозначена символом
![]()
Построим два
прямоугольника CHED
и CMKD.
Площадь
первого из них равна f(x)
x,
а площадь
второго равна
![]() .
Поскольку площадь криволинейной трапеции
CHKD
не меньше
площади прямоугольника CHED
и не больше
площади прямоугольника CMKD,
можно записать
неравенство
.
Поскольку площадь криволинейной трапеции
CHKD
не меньше
площади прямоугольника CHED
и не больше
площади прямоугольника CMKD,
можно записать
неравенство
![]()
Разделим обе части
этого неравенства на
![]() и найдем
пре-
и найдем
пре-
318


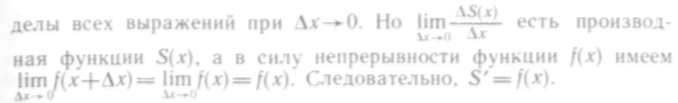
Итак, производная площади криволинейной трапеции равна функции, задающей верхнюю границу трапеции.
Поэтому площадь криволинейной трапеции есть одна из первообразных функции, задающей верхнюю границу трапеции, и может быть вычислена с помощью интегрирования:
![]()

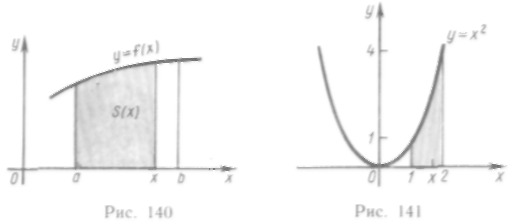
221. Используя
равенство
![]() ,
вычислить площадь криволинейной
трапеции, ограниченной линиями у
= х2,
х=1, х=2,
у = 0.
,
вычислить площадь криволинейной
трапеции, ограниченной линиями у
= х2,
х=1, х=2,
у = 0.

319
2. Вычисление площади криволинейной трапеции

320
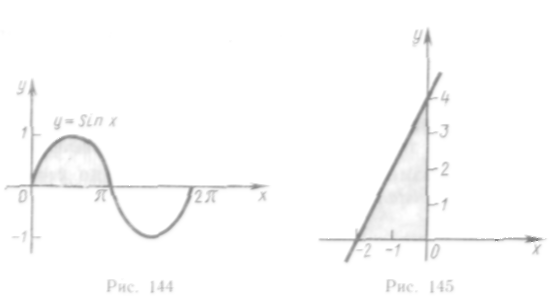

3. Определение определенного интеграла

11-1356 321
![]()
Это приращение принято называть определенным интегралом.

![]()
Равенство (2) называется формулой Ньютона—Лейбница.
Все методы интегрирования, используемые при нахождении неопределенных интегралов, применяются и при вычислении определенных интегралов. Числовое значение определенного интеграла зависит от вида функции, стоящей под знаком интеграла, и от значений верхнего и нижнего пределов и не зависит от обозначения переменной.
322
229—237. Вычислить определенные интегралы:

Если
формулу Ньютона —Лейбница сравнить с
формулой (1),
то очевидно, что
![]() и есть
площадь криволинейной трапеции,
определяемой графиком функции
и есть
площадь криволинейной трапеции,
определяемой графиком функции
![]() на отрезке
[а, Ь].
на отрезке
[а, Ь].
Таким образом,
если функция
![]() положительна,
то определенный интеграл представляет
собой площадь криволинейной трапеции.
В этом заключается геометрический смысл
определенного интеграла.
положительна,
то определенный интеграл представляет
собой площадь криволинейной трапеции.
В этом заключается геометрический смысл
определенного интеграла.
Тогда площадь криволинейной трапеции можно вычислить по формуле
![]()
238. Вычислить
площадь криволинейной трапеции,
ограниченной осью Ох,
прямыми
х=—1, х = 2 и
параболой
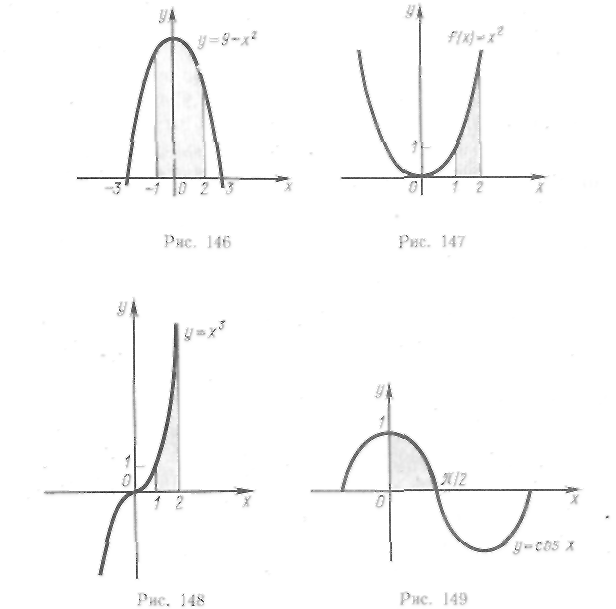
![]() (рис. 146).
(рис. 146).
Решение.
Так
как на отрезке [ — 1, 2] функция
![]() принимает
положительные значения, то для вычисления
искомой площади 5
принимает
положительные значения, то для вычисления
искомой площади 5
11* 323
воспользуемся формулой (3):
![]()
Применяя формулу Ньютона — Лейбница, находим

324
