2. Примеры интегрирования подстановкой

Естественно возникает вопрос: как правильно выбрать постановку? Это достигается практикой в интегрировании. Все же можно установить ряд общих правил и некоторых приемов для частных случаев интегрирования.

Правило интегрирования способом подстановки состоит в сле­дующем:

1°. Определяют, к какому табличному интегралу приводится данный интеграл (предварительно преобразовав подынте­гральное выражение, если нужно).

2°. Определяют, какую часть подынтегральной функции заме­нить новой переменной, и записывают эту замену.

3°. Находят дифференциалы обеих частей записи и выража­ют дифференциал старой переменной (или выражение, содержащее этот дифференциал) через дифференциал новой переменной.

4°. Производят замену под интегралом.

5°. Находят полученный интеграл.

6⁰. В результате производят обратную замену, т. е. переходят к старой переменной. Результат полезно проверить диф­ференцированием. Частные приемы будут рассмотрены по ходу решения при­меров.

146—206. Найти неопределенные интегралы способом подста­новки:

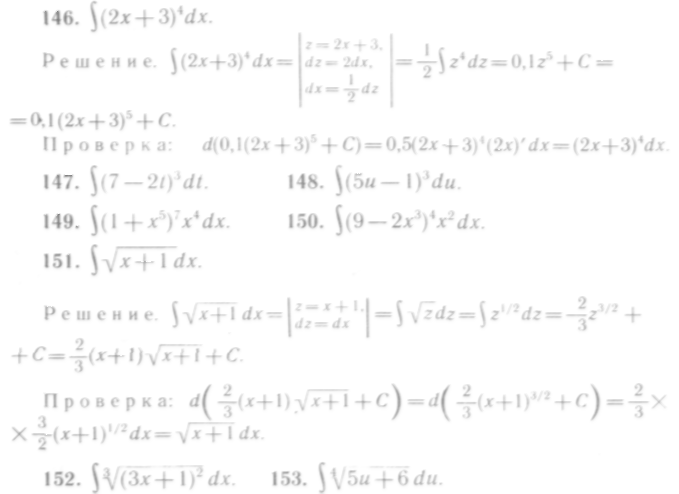
312

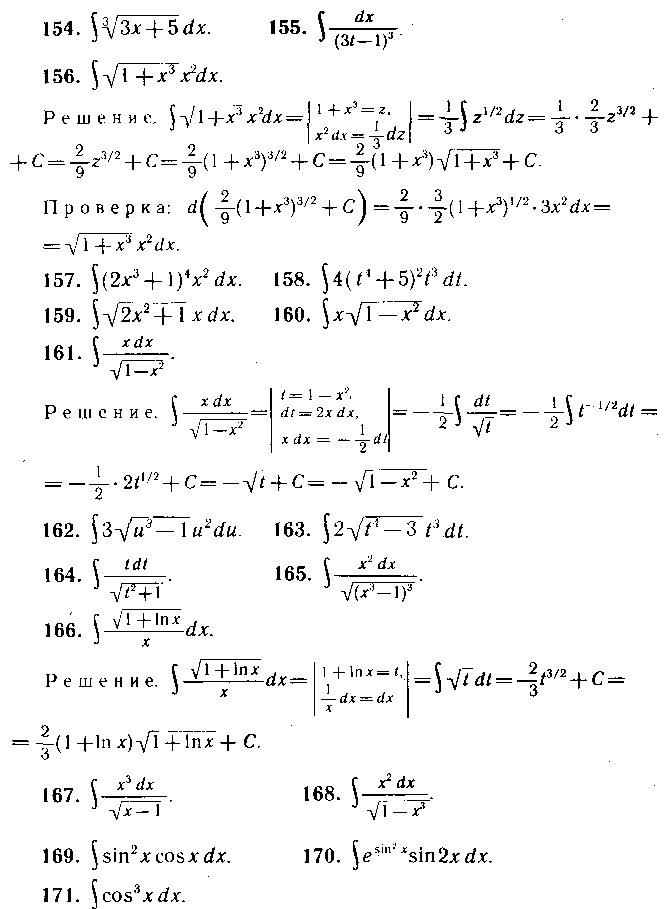
Решение. Сначала преобразуем подынтегральную функцию: . Далее находим

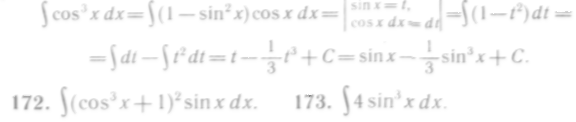
313

Формулы (1) и (2) полезно запомнить и пользоваться ими как табличными интегралами.

314

Решение. Приведем данный интеграл к табличному виду X:

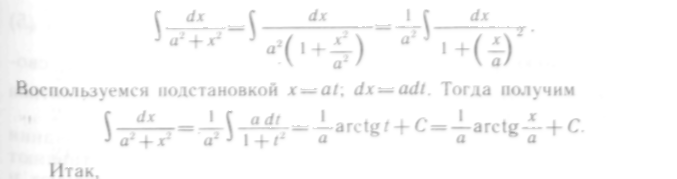
315

Решение. Приведем данный интеграл к табличному виду IX:

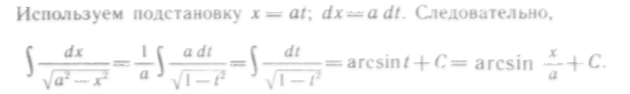
Итак,

Формулы (3) и (4) полезно запомнить и пользоваться ими как табличными интегралами.

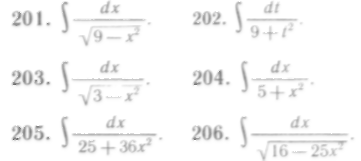
3. Способ интегрирования по частям

При интегрировании функций, содержащих произведения, ло­гарифмы и обратные тригонометрические функции, бывает удоб­но воспользоваться способом интегрирования по частям.

Выведем формулу интегрирования по частям.

Интегрируя обе части равенства , получим

откуда

С помощью формулы (5) нахождение интеграла сводится к нахождению интеграла , который может оказаться или проще данного, или даже известным.

При практическом использовании формулы интегрирования по частям данное подынтегральное выражение представляют в виде произведения двух сомножителей, которые обозначают u и dv. Множитель и стараются выбрать так, чтобы и' было проще, чем и.

316

207—220. Применяя формулу интегрирования по частям, найти интегралы:

Если же в этом интеграле сделать другую замену: , то легко убедиться, что полученный интеграл окажется сложнее исход­ного, т. е. замена окажется неудачной Умение определить целесообраз­ность той или иной замены приходит с приобретением навыка.

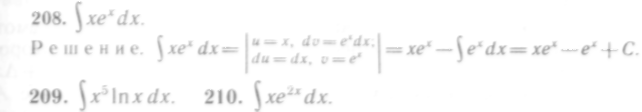
Иногда формулу интегрирования по частям приходится при­менять дважды.

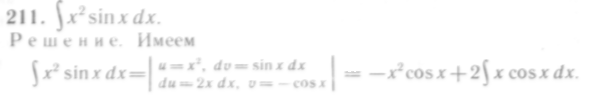
Для нахождения полученного в правой части равенства интеграла снова интегрируем по частям:

(см. решение примера 207). В результате получаем окончательный ответ:

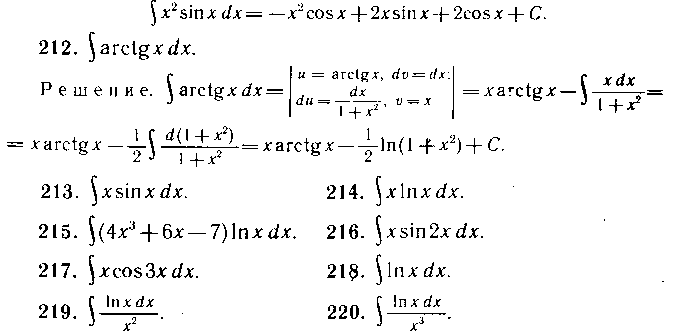
317

§ 6. Определенный интеграл и его геометрический смысл

• I. Криволинейная трапеции и ее площадь

0 2. Вычисление площади криволинейной трапеции

• 3. Определение определенного интеграла