2. Выделение из семейства кривых с одинаковым наклоном линии, проходящей через конкретную точку

Под наклоном кривой понимают тангенс угла наклона каса­тельной к этой кривой в данной точке.

Из дифференциального исчисления известно, что наклон к кривой (угловой коэффициент касательной) в точке с абсциссой х равен значению производной в этой точке, т. е.

Рассмотрим теперь обратную задачу: зная наклон к кривой в любой ее точке как функцию абсциссы этой точки, т. е. зная, что , найти уравнение кривой.

307

130. Из семейства кривых, имеющих наклон, равный 2х, выделить ту, которая проходит через точку (3; 5).

131. Найти уравнение кривой, проходящей через точку (1;4), если угловой коэффициент касательной в каждой точке кривой задается функцией Зд:².

132. Найти уравнение кривой, проходящей через точку (2; 3), зная, что угловой коэффициент касательной к кривой, проведен­ной в любой ее точке, равен х² — 1.

133. Из семейства кривых, имеющих наклон, равный выделить ту, которая проходит через точку (1;4).

134.На промежутке (0, ) найти такую первообразную функ­ции , график которой проходит через точку (1; 3).

3. Составление уравнения движения тела по заданному уравнению скорости или ускорения его движения

Из дифференциального исчисления известно, что и , где — соответственно путь, скорость и ускорение движущегося тела. Тогда закон движения тела по заданной скорости можно найти интегрированием, а по заданному ускорению — двукратным интегрированием.

Это искомое уравнение.

В следующих задачах данного раздела рассматривается пря­молинейное движение.

308

309

§5. Интегрирование подстановкой и по частям

• 1. Способ подстановки (замены переменной)

• 2. Примеры интегрирования подстановкой

• 3. Способ интегрирования по частям

1. Способ подстановки (замены переменной)

Рели заданный интеграл с помощью алгебраических преоб­разований трудно или невозможно свести к одному или несколь­ким табличным интегралам, то для его отыскания применяют особые способы, одним из которых является способ подстановки (замены переменной).

310

Заметим, что все способы интегрирования имеют целью свести данный интеграл к табличному с помощью тех или иных искус­ственных приемов.

Способ подстановки заключается в следующем: заменяют новой переменной такую часть подынтегральной функции, при дифференцировании которой получается оставшаяся часть подынтегрального выражения (не считая постоянного множите­ля, на который всегда можно умножить и разделить подынтег­ральное выражение).

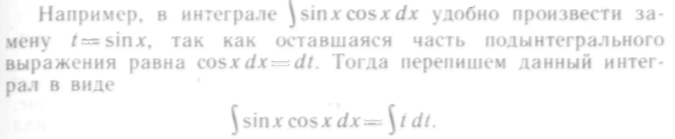
Полученный интеграл является табличным: он находится по формуле I:

Далее, произведя обратную замену , получим ответ:

Решение этого примера можно кратко оформить так:

Напомним, что если при интегрировании одной и той же функции разными способами получили различные результаты, то необходимо показать, что они отличаются на постоянную вели­чину.

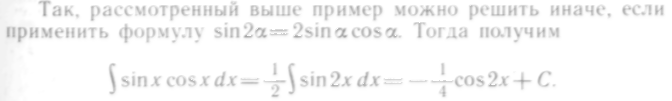
Результат по виду отличается от найденного ранее; однако, преобразуя первый результат, имеем

Отсюда видно, что разность функций равна , т. е. постоянному числу.

Следует иметь в виду, что мы уже встречались с простейшими случаями подстановок, только выполняли их в другом оформле­нии записи (см. примеры 88, 89, 107, 108).

311