3. Интегрирование по формуле II

Решение. Разделив числитель почленно на х, представим подынтегральную функцию в виде суммы двух дробей:

Разобьем последний интеграл на сумму двух интегралов и приме­ним формулы I и II. Тогда получим

Продифференцировав результат, легко убедиться, что решение верно.

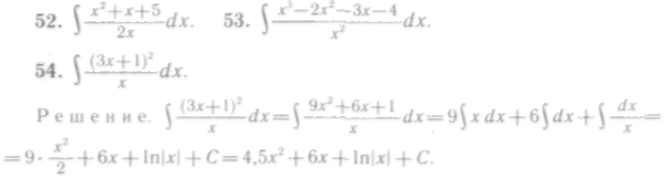
300

Замечание. При выполнении интегрирования нужно твердо помнить, что применение табличных интегралов возможно только тогда, когда под знаком дифференциала стоит выражение, отвечающее определенным тре­бованиям. Так, при использовании формулы I под знаком дифференциала должно быть основание степени, при применении формулы II в числителе должен находиться дифференциал знаменателя и г. д.

Например:

4. Интегрирование по формулам III и IV

Справедливость формул III и IV, т. е.

легко проверяется дифференцированием их правых частей:

Отметим, что формула III является частным случаем фор­мулы IV при а = е.

Здесь были применены свойства 3 и 2 (разложение на сумму интег-

301

ралов и вынесение постоянного множителя за знак интеграла), а затем для первого интеграла формула I, для второго формула III.

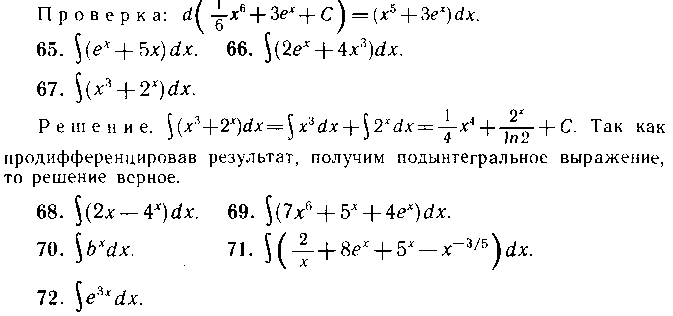
Решение. Согласно сделанному ранее замечанию, под знаком дифференциала должен стоять показатель степени, но d(3x) = 3dx. Следовательно, необходимо добавить множитель 1/3. Тогда получим

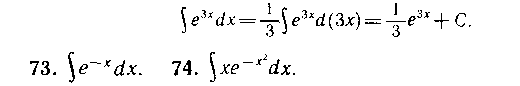
5. Интегрирование по формулам V и VI

Справедливость формул V и VI, т. е.

также проверяется дифференцированием их правых частей:

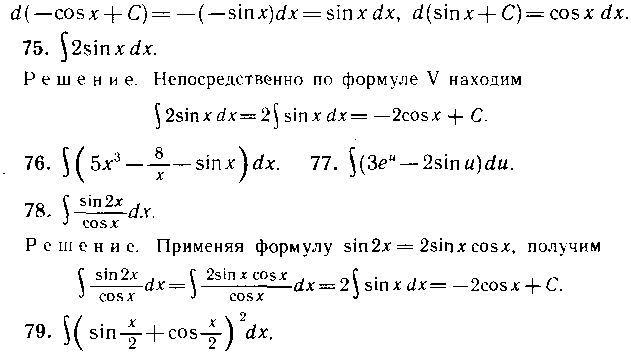
Решение. Имеем

302

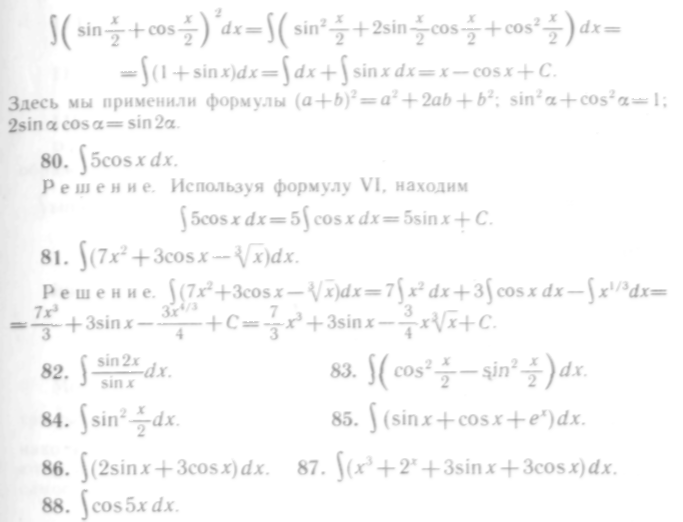
Решение. Согласно сделанному ранее замечанию, под знаком дифференциала должен находиться аргумент подынтегральной функции. Следовательно,

6. Интегрирование по формулам VII и VIII

Справедливость формул VII и VIII, а именно

проверяется дифференцированием их правых частей:

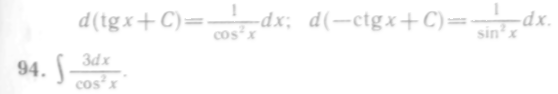
303

304

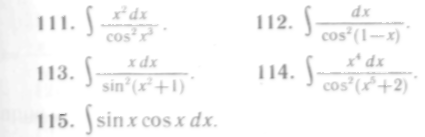
Решение. Проинтегрируем, применяя различные приемы пре­образования подынтегрального выражения:

7. Интегрирование по формулам IX и X

Справедливость формул IX и X, т. е.

проверяется дифференцированием их правых частей:

Продифференцировав результат, получим подынтегральное выра­жение. Следовательно, решение верное.

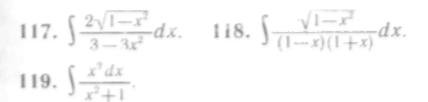
Решение. Имеем

305

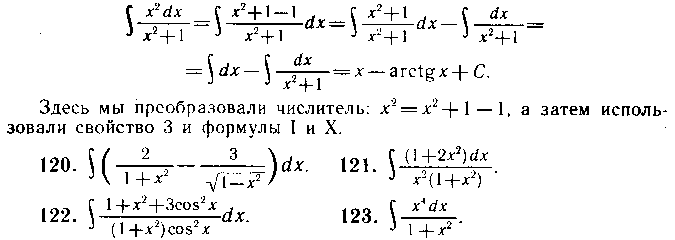
§ 4. Приложения неопределенного интеграла

• 1. Нахождение первообразной по начальным условиям

• 2. Выделение из семейства кривых с одинаковым наклоном линии.

проходящей через конкретную точку

• 3. Составление уравнения движения тела по заданному уравнению

скорости или ускорения его движения

. 1. Нахождение первообразной по начальным условиям

Как известно, при интегрировании функции получается совокупность ее первообразных. Для выделения из всей сово­купности конкретной первообразной задают дополнительные дан­ные, так называемые начальные условия.

При решении таких задач используют следующий алгоритм:

1°. Находят неопределенный интеграл от заданной функции.

2°. Вычисляют величину С, подставляя начальные условия в полученную совокупность первообразных для заданной функции.

3⁰. Находят искомую первообразную, заменяя в совокупности первообразных постоянную интегрирования ее вычислен­ным значением 124. Найти функцию, производная которой равна если известно, что при функция принимает значение, равное 25.

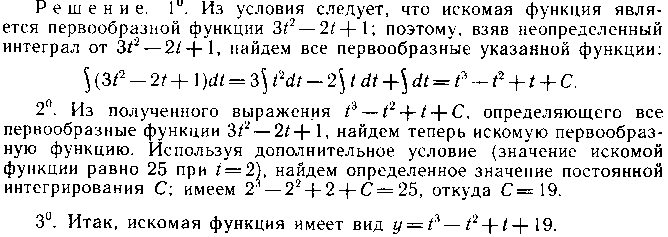
306