§ 3. Основные табличные интегралы

• 1. Основные формулы интегрирования

• 2. Интегрирование по формуле I

• 3. Интегрирование по формуле II

• 4. Интегрирование по формулам 111 и IV

• 5. Интегрирование по формулам V и VI

• 6. Интегрирование по формулам VII и VIII

• 7. Интегрирование по формулам IX и X

1. Основные формулы интегрирования

Из определения интеграла следует, что для того чтобы проин­тегрировать функцию, нужно найти ее первообразную. Для ряда функций это легко сделать, используя соответствующую фор­мулу дифференцирования.

296

Например, мы знаем, что ; отсюда следует, что

Итак, формулы интегрирования получаются обращением соот­ветствующих формул дифференцирования. Выпишем в таблицу основные интегралы.

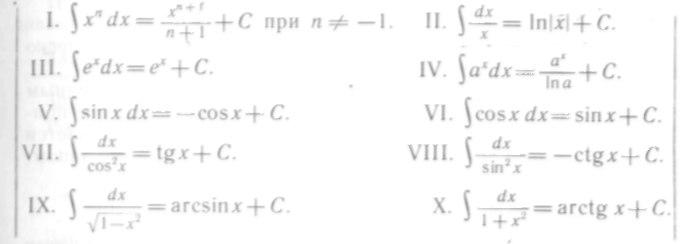
Интегралы, приведенные в этой таблице, называются таблич­ными интегралами.

Для вывода этих формул, как уже отмечалось, используется свойство 5 неопределенного интеграла, а именно дифференци­рование правой части равенства. Производная правой части ра­венства дает подынтегральную функцию, а дифференциал — подынтегральное выражение.

Формула I справедлива при любом п, кроме п = — 1, так как в этом случае знаменатель обращается в нуль и выражение теряет смысл. Для доказательства найдем производную правой части равенства:

Мы получили подынтегральную функцию; следовательно, фор­мула верна.

Случаю п = — 1 соответствует формула II:

Чтобы найти , заметим, что функция — непрерывна в промежутках и , причем в каждом из них она имеет первообразную.

В промежутке этой первообразной, очевидно, является функция 1плг, так как , т. е. при

В промежутке ( - ), 0) первообразной по отношению к

297

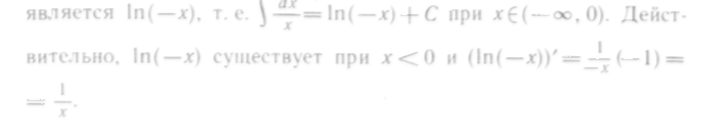
Итак, оба промежутка непрерывности подынтегральной функ­ции объединяются записью

Справедливость всех остальных табличных интегралов легко проверить, если продифференцировать их правые части.

Вычисление интегралов способом приведения их к табличным с помощью преобразования подынтегрального выражения и при­менения свойств 2 и 3 неопределенного интеграла называется непосредственным интегрированием. При этом полезно запом­нить, что (формула I при п = 0).

23. Найти интеграл и сделать проверку.

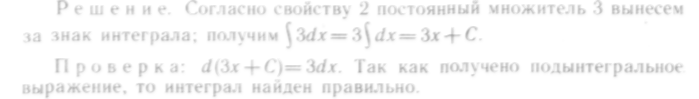
2. Интегрирование по формуле I

На практике чаще всего приходится интегрировать степенную функцию, т. е. применять формулу I.

24—123. Найти интегралы и проверить результаты дифференциро­ванием.

298

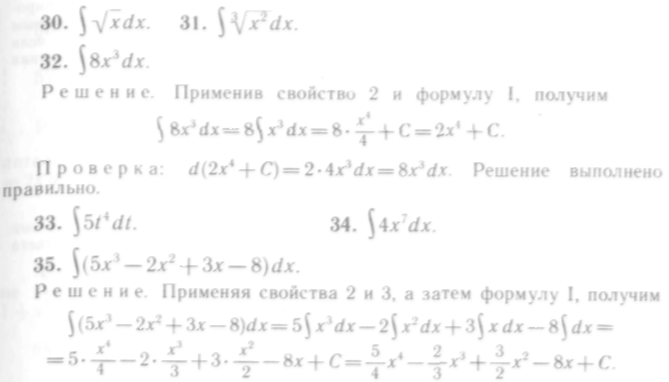
Здесь С — алгебраическая сумма четырех произвольных постоянных слагаемых, являющихся составной частью каждого интеграла.

Продифференцировав этот результат, получим подынтегральное вы­ражение, т. с. решение верное.

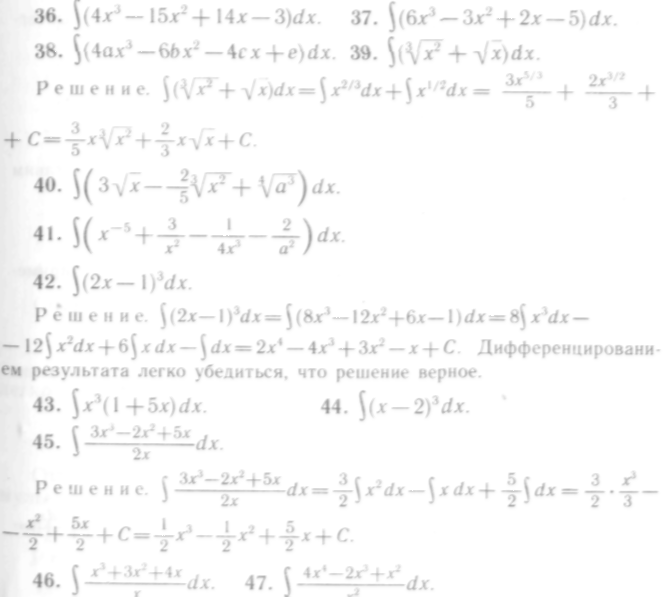
299

Замечание. Следует иметь в виду, что разные способы интегриро­вания одной и той же функции иногда приводят к функциям, различным по своему виду. Это кажущееся противоречие можно устранить, если показать, что разность между полученными функциями есть постоянная величина.

Например,

Найдем этот интеграл другим способом:

Результаты имеют различный вид, однако легко проверить, что они отличаются на постоянную величину, равную 1, и, значит, оба ответа верны.