2. Определенный интеграл как предел суммы

Рассмотрим криволинейную трапецию, заданную непрерыв­ной неотрицательной функцией , на отрезке [а, Ь]. Разобьем этот отрезок на п равных частей точками х₀ = а, х₁, _X2..., х_n=b и проведем через эти точки прямые, параллельные оси ординат (рис. 190). Тогда данная криволинейная трапеция разобьется на п полос, также представляющих собой криволинейные тра­пеции. Заменим каждую из этих полос прямоугольником осно­вание которого то же, что у соответствующей полосы, и равно а высота совпадает с одной из ее ординат – левой (рис. 191) или правой f(x_k) (рис. 192), где к – порядковый номер полосы (k= 1,2,..., п)

Будем увеличивать число точек разбиения отрезка [а Ь] так, чтобы х 0. При этом длины ординат f(x_k-1) и f(х_к) будут отличаться друг от друга тем меньше, чем больше п. Таким образом, площадь k-го прямоугольника равна f(x_k)Ax (для определенности в качестве высоты прямоугольника мы выбрали пра­вую ординату).

Рассмотрим сумму площадей всех таких прямоугольников:

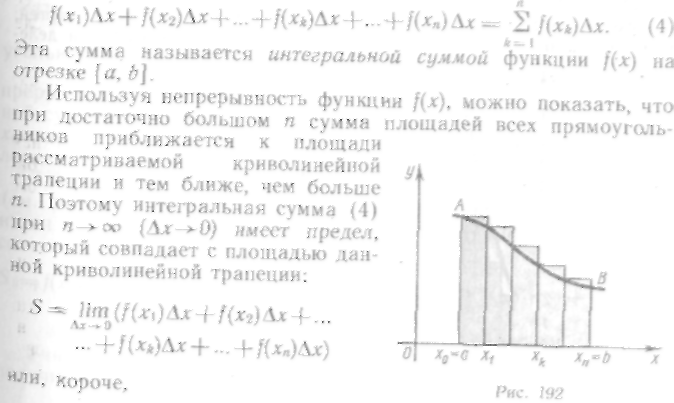
345

343. Найти значение интегральной суммы для функции у= х²+1 при делении отрезка [1,3] на две части.

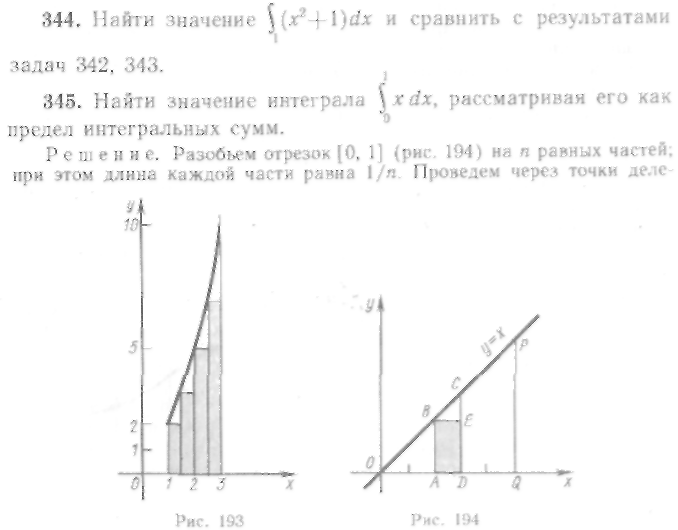
346

3. Метод прямоугольников

Решение многих задач сводится к вычислению определенных интегралов, точное выражение которых сложно, требует длитель­ных вычислений и не всегда оправдано практически. В этом слу­чае часто бывает вполне достаточно найти их приближенное значение.

Пусть, например, необходимо вычислить площадь, ограничен­ную линией, уравнение которой неизвестно. В этом случае можно заменить данную линию более простой, уравнение которой из­вестно. Площадь полученной, таким образом криволинейной тра­пеции принимается за приближенное значение искомого* интег­рала.

347

Какова же погрешность, возникающая при замене интеграла его интегральной суммой? Не останавливаясь на отыскании этой погрешности, заметим, что если функция монотонна, то

точное значение интеграла заключено между суммой (8) и суммой

которая получается, если в криволинейной трапеции дугу АВ кривой заменить ломаной ступенчатой фигурой, изображенной на рис. 192. Следовательно,

Итак, чтобы найти приближенное значение интеграла, нужно:

1. разделить отрезок интегрирования [а, Ь] на п. равных частей точками ;

2. в ычислить значения подынтегральной функции в точках деления, т.е. найти ,

3) воспользоваться одной из следующих приближенных формул:

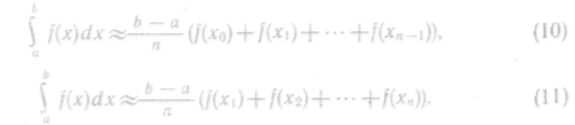
Соотношения (10) и (11) называются формулами прямо­угольников.

348

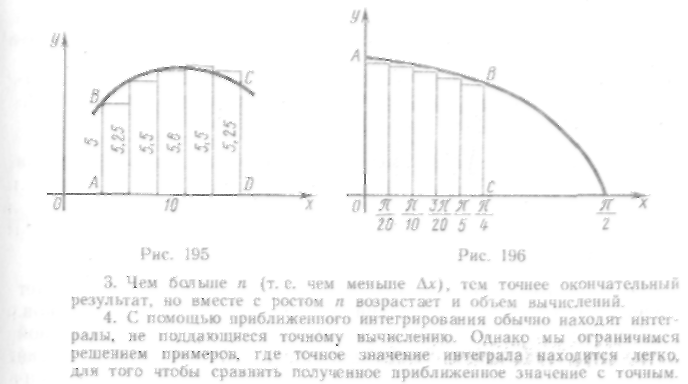
347. Вычислить площадь фигуры A BCD по данным, представ­ленным на рис. 195.

Решение. Разобьем основание AD, равное. 10 см, на 5 равных частей и проведем через точки деления прямые, параллельные оси ординат. Применяя формулу (10), получим приближенное значение искомой площади:

Найти относительную погрешность вычисления.

349

4. Метод трапеций

Этот метод приближенного интегрирования обычно дает более точное значение интеграла, чем метод прямоугольников.

Заменим дугу АВ кривой ломаной линией, вписанной в эту дугу (рис. 197). Тогда площадь криволинейной трапеции заменится суммой площадей обычных (т. е. прямолинейных) тра­пеций. Площади этих трапеций определяются по формулам

где у_о, у₁,…y_п — ординаты, соответствующие значениям функ­ции в точках деления. Сумму площадей всех элементар­ных трапеций можно принять за приближенное значение площа­ди криволинейной трапеции, а следовательно, и за приближен­ное значение определенного интеграла, т. е.

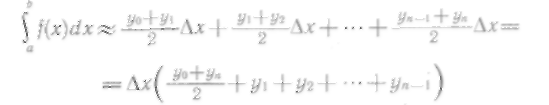
или

Формула (12) называется формулой трапеций.

350

Точное значение интеграла определяем по формуле Ньютона — Лейбница:

Найдем относительную погрешность приближенного вычисления:

353. Вычислить но формуле трапеций площадь фигуры A BCD по данным, представленным на рис. 196.

354. Вычислить по формуле трапеций интеграл 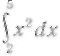. Срав­нить с результатом решения этой же задачи методом прямо­угольников(см. пример 349).

3 51

Абсолютная погрешность этого приближенного значения (по не­достатку) равна 3,1817, а относительная

Согласно формуле прямоугольников (11), получим

Здесь абсолютная погрешность (по избытку) равна 2,8183, а относи­тельная

По формуле трапеций (12) находим

352

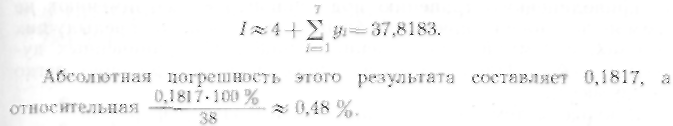
359. Применяя формулу Ньютона — Лейбница и приближен­ные формулы прямоугольников и трапеций, вычислить интеграл разбив промежуток интегрирования на 10 равных частей.

360. Вычислить интеграл по формуле Ньютона—Лейб­ница и по приближенным формулам прямоугольников и трапе­ций, разбив промежуток интегрирования на 10 равных частей.

361. Вычислить интеграл по формуле Ньютона — Лейбница и по приближенным формулам прямоугольников и тра­пеций, разбив промежуток интегрирования на 10 равных частей.

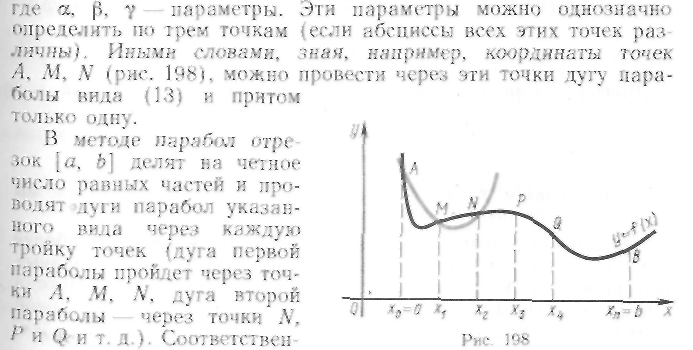
5. Метод парабол

Из других методов приближенного интегрирования следует отметить метод парабол (который также называют методом Симпсона).

Его сущность заключается в том, что отрезки прямых, огра­ничивающих элементарные трапеции сверху, заменяют дугами парабол, оси которых параллельны оси Оу.

Из школьного курса алгебры известно, что уравнения таких парабол имеют вид

12—1356 353

но криволинейную трапецию под кривой заменяют не суммой площадей прямолинейных фигур, как в предыдущих методах, а суммой криволинейных трапеций, ограниченных ду­гами парабол. Площади таких криволинейных трапеций легко вычисляются.

В курсе математического анализа выводится формула

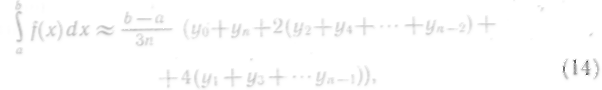
Вычисление интеграла по формуле Ньютона — Лейбница дает

Таким образом, применяя формулу Симпсона, в данном случае мы получили точное значение интеграла.

Заметим, что хотя метод прямоугольников является наиболее простым методом приближенного вычисления определенных интегралов, он дает наименее точные результаты. Выбор метода приближенного интегрирования зависит от подынтегральной функции и требуемой точности расчета.

354