Глава V Интеграл и его приложения

§ 1. Первообразная

• 1. Дифференцирование и интегрирование — взаимно обратные действия

• 2. Определение первообразной функции

• 3. Неоднозначность нахождении первообразной

1. Дифференцирование и интегрирование — взаимно обратные действия

Из школьного курса математики известно, что каждому мате­матическому действию соответствует обратное ему действие. Так, вычитание есть действие, обратное сложению, деление - умножению и т. д.

В гл. IV было рассмотрено новое действие — дифференци­рование. Основной задачей дифференциального исчисления явля­ется нахождение производной или дифференциала заданной функции. Для дифференцирования существует обратное дей­ствие — интегрирование: нахождение функции но заданной ее производной или дифференциалу. Мы знаем, например, как по заданному закону движения найти его скорость

Это — задача дифференцирования. Обратная задача — нахож­дение закона движения по заданной скорости — решается интег­рированием. Таким образом, если в процессе дифференцирова­ния решается задача об отыскании скорости изменения функции, вызываемого изменением аргумента, то задачей интегрирования является нахождение самой функции по заданной скорости ее изменения.

2. Определение первообразной

Функцию, восстанавливаемую по заданной ее производной или дифференциалу, называют первообразной.

290

1. Найти первообразную функции ,

Замечание. Если сказано, что F(x) — первообразная функции ,но не указано, в каком именно интервале, то под этим интервалом в дальнейшем будет подразумеваться любой интервал, в котором функции определена.

²⁹¹

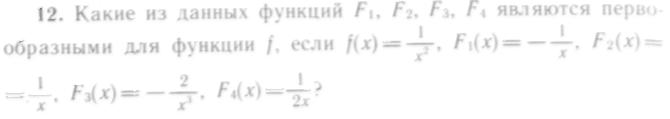
3. Неоднозначность нахождения первообразной

Как всякое обратное действие, интегрирование вносит некото­рое осложнение. Вспомним, как начинается изучение действий над числами. Сначала изучают только целые положительные числа. Наиболее простое действие — сложение — не вносит ника­ких затруднений. Однако стоит только перейти к обратному дей­ствию вычитанию, как встречается первое затруднение: вычесть из меньшего числа большее невозможно. Чтобы преодолеть эту трудность, в алгебре вводят отрицательные числа и вычитание становится возможным, например 1 —3=—2. При умножении целых чисел не встречается никаких затруднений; обратное же действие —деление —сразу вносит трудность. Оказывается, что далеко не все числа делятся друг на друга. Деление становится возможным с введением дробных чисел, например . Еще большие затруднения появляются при извлечении корня — действии, обратном возведению числа в целую положительную степень; здесь уже появляются затруднения в знаках. Так, ко­рень четной степени из положительного числа имеет два знака, а корень четной степени из отрицательного числа не имеет дей­ствительного значения. Чтобы стало возможным извлечение корней целой положительной степени из действительных чисел, требуется ввести понятия об иррациональном числе, о мнимой единице, о мнимом числе и т. д. Интегрирование как действие, обратное дифференцированию, также вносит осложнение.

Дифференцирование функции — однозначная операция, т. е. если функция имеет производную, то только одну. Это утвержде­ние непосредственно следует из определений предела и производ­ной: если функция имеет предел, то только один. Обратная опе-

2 92