8. Вычисление пределов

Сначала рассмотрим примеры непосредственного нахождения предела функции в точке.

120. Найти

Решение. Для нахождения предела данной функции заменим аргумент х его предельным значением:

121. Найти

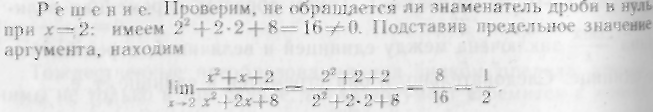
Рассмотрим теперь такие примеры, когда применение свойств предела становится возможным лишь после некоторых предвари­тельных преобразований.

122. Найти

Решение. Здесь пределы числителя и знаменателя при равны нулю. Умножив числитель и знаменатель на выражение, сопряженное числителю, получим

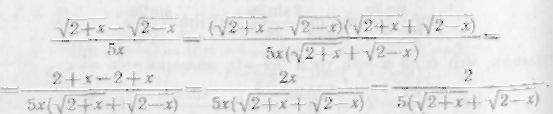
Следовательно,

192

123. Найти

Решение. Здесь имеем неопределенность типа 0/0. Для того чтобы раскрыть эту неопределенность, разложим числитель и знаме­натель дроби на множители и до перехода к пределу сократим дробь _на множитель х—2. В результате получим

Итак, чтобы найти предел частного двух функций, где преде­лы делимого и делителя равны нулю, нужно преобразовать функ­цию таким образом, чтобы выделить в делимом и делителе сомно­житель, предел которого равен нулю, и, сократив дробь на этот сомножитель, найти предел частного.

124. Найти .

Решение. Непосредственная подстановка х= —2 показывает, что имеет место неопределенность вида 0/0. Разложив числитель на множители и сократив дробь, находим

Здесь предел делителя равен нулю. Таким образом, знаменатель дроби неограниченно убывает и стремится к нулю, а числитель приближается к —1. Ясно, что вся дробь неограниченно растет, что условно записы­вается так:

125—130. Найти пределы:

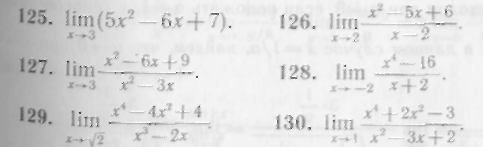
Перейдем к примерам нахождения предела функции на бесконечности.

131. Найти

Решение. При имеем неопределенность вида . Чтобы

Раскрыть эту неопределенность, разделим числитель и знаменатель когда получим

7-1356 193

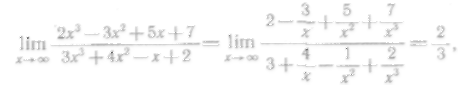
так как при

132—133. Найти пределы:

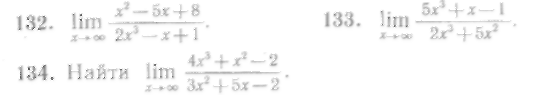
Решение. Разделив числитель и знаменатель на х⁵ и перейдя к пределу, получим

поскольку числитель последней дроби стремится к пределу, отличному от нуля, а знаменатель — к нулю.

135. Найти

Решение. При стремлении аргумента х к бесконечности имеем неопределенность вида . Чтобы раскрыть ее, разделим числитель

и знаменатель дроби на х. Тогда получим

так как

136. Найти

Решение. Предельный переход при всегда можно заменить

предельным переходом при , если положить способ замены

переменной).

Так, полагая в данном случае найдем, что при

Следовательно,

194

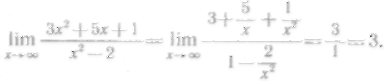
II способ. Положим ; тогда при . Значит,

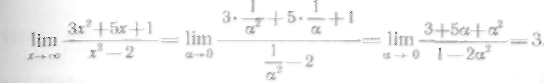
138—141. Найти пределы:

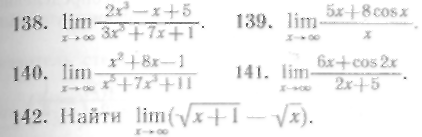
Решение. Здесь требуется найти предел разности двух величин, стремящихся к бесконечности (неопределенность вида ). Умно­жив и разделив данное выражение на сопряженное ему, получим

Следовательно,

Рассмотрим примеры, в которых используются замечательные пределы.

7* 195

145. Найти

Решение. Преобразуем числитель к виду

II способ. Преобразуем числитель следующим образом:

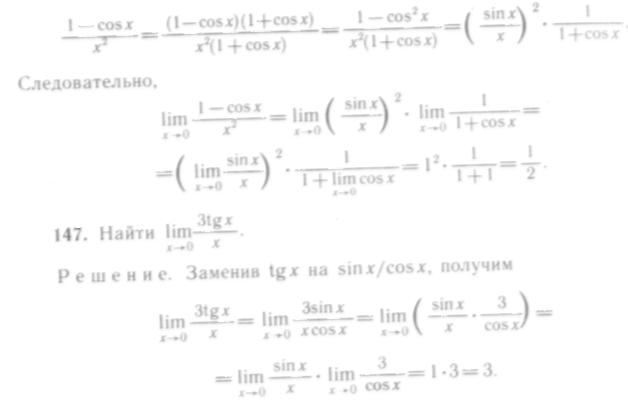
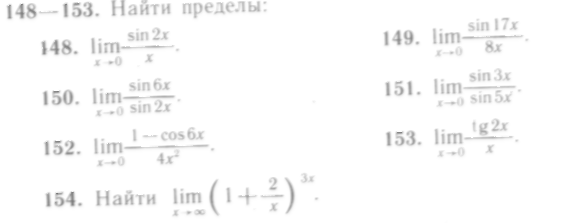
Решение. Имеем

196

§ 3. Производная

• 1. Задачи, приводящие к понятию производной

• 2. Определение производной

• 3. Общее правило нахождения производной

• 4. Частное значение производной

• 5. Связь между непрерывностью и дифференцируемостью функции