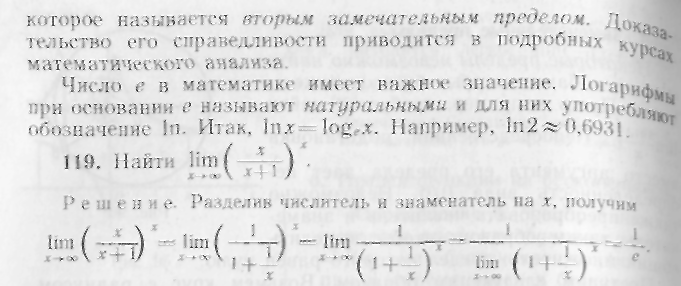5. Понятие о непрерывности функции

Наглядное представление о непрерывной функции состоит в том, что график такой функции можно начертить одним непре­рывным движением, не отрывая карандаша от бумаги. В против­ном случае имеет место графическое изображение разрывной функции. На рис. 91 изображена некоторая непрерывная функ­ция, на рис. 92 и 93 — разрывные функции.

Непрерывное изменение переменной величины легко предста­вить себе интуитивно. В самом деле, когда мы говорим: «Тем­пература воды при нагревании изменяется непрерывно» — мы имеем в виду, что за достаточно малый промежуток времени температура воды изменится достаточно мало, т. е. если температуру воды рассматривать как функцию времени, то в изменении этой функции наблюдается постепенность.

Примерами непрерывных функций могут служить также раз- личные законы движения тел , выражающие зависимость

пройденного пути s от времени t. Одной из особенностей этой

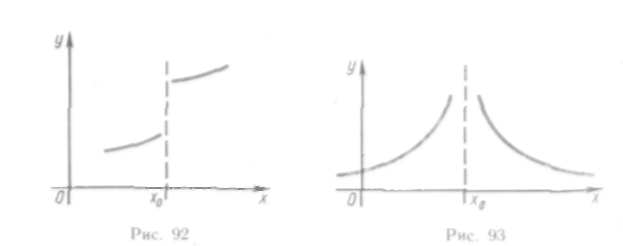
186

зависимости является то, что малому приращению времени соответствует малое приращение пути, т. е. график функции изображается непрерывной линией.

Определение 3. Функция называется непрерывной в точке х=х₀, если:

1) эта функция определена в точке х=х_о (т. е. опреде­ ленному значению аргумента х, равному хо, соответствует вполне определенное значение функции у, равное );

2) приращение функции в точке стремится к нулю при , т. е.

Кратко свойство непрерывности функции можно выразить так: функция называется непрерывной в данной точке, если при . Из рис. 90 видно, что если точке М приближается по кривой к точке М, то как угодно уменьшаются, т. е. стре-

мятся к нулю, и данная функция в точке М является непре­рывной.

Итак, геометрически непрерывность функции означает, что ординаты двух точек графика сколь угодно мало отли­чаются друг от друга, если достаточно мало отличаются их абс­циссы. Поэтому график непрерывной функции представляет со­бой сплошную линию без разрывов.

Часто пользуются другим, равносильным приведенному, опре­делением непрерывности функции в точке.

187

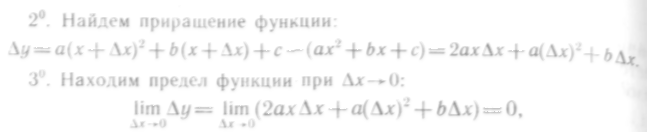
105. Исследовать на непрерывность функцию

i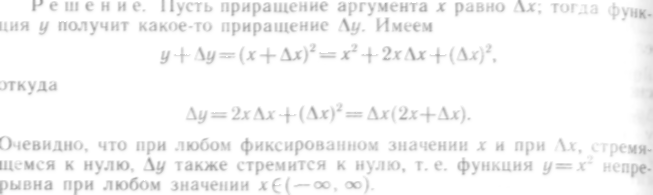

106. Показать, что функция непрерывна при всех х. Решение. Найдем приращение функции:

107—110. Исследовать на непрерывность функции:

Можно доказать, что каждая элементарная функция непре­рывна в любой точке из ее области определения.

188

на землю. Эта скорость, вообще говоря, есть непрерывная функция времени, но в момент удара можно считать, что она мгновенно (скачком) падает до нуля, т.е. функция скорости терпит

разрыв.

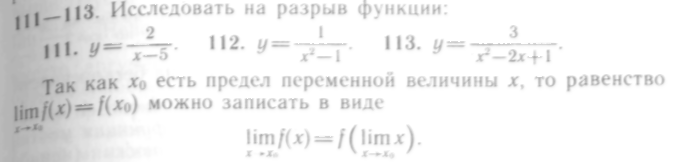
Эта формула выражает очень важное для вычисления пре­делов правило: если функция непрерывна, то при отыскании ее предела можно вместо аргумента подставить его предельное зна­чение.

В дальнейшем мы будем пользоваться этим приемом, посколь­ку он значительно упрощает вычисления предела функции.

114. Вычислить

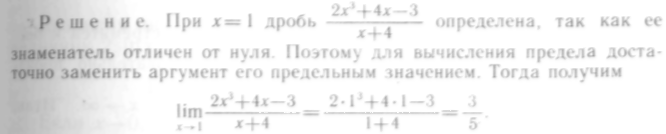
Указанное правило вычисления пределов нельзя применять в следующих случаях:

1) если функция при не определена;

2) если знаменатель дроби при подстановке оказывается равным нулю;

3) если числитель и знаменатель дроби при подстановке одновременно оказываются равными нулю или бесконечности.

В таких случаях пределы функций находят с помощью раз­умных искусственных приемов.

115. Найти

Решение. Здесь непосредственный переход к пределу невозможен поскольку предел делителя равен нулю:

предел делимого также равен нулю: . Значит, имеет неопределенность вида 0/0. Однако отсюда не следует, что данная функция не имеет предела; для его нахождения нужно предварительно преобразовать функцию, разделив числитель и знаменатель на выражение х-3:

189

116. Найти

117. Найти

190

Разделив все члены этого неравенства на положительную величину , получим

Если , то _. Таким образом, переменная величина заключена между единицей и величиной, стремящейся к единице. Следовательно, и она стремится к единице, т.е.

Этот предел называют первым замечательным пределом. 118. Найти

Решение. Приведем этот предел к виду (1). Для этого числи­тель и знаменатель дроби умножим на 2, а постоянный множитель 2 внесем на знак предела. Имеем

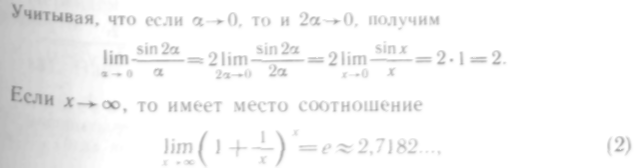
191