§ 2. Предел и непрерывность функции

• 1. Предел переменной величины

• 2. Основные свойства пределов

• 3. Предел функции в точке

• 4. Приращение аргумента и приращение функции

• 5. Понятие о непрерывности функции

• 6. Предел функции на бесконечности

• 7. Замечательные пределы

• 8. Вычисление пределов

1. Предел переменной величины

Пусть переменная величина х в процессе своего изменения неограниченно приближается к числу 5, принимая при этом сле­дующие значения: 4,9; 4,99; 4,999; ... или 5,1; 5,01; 5,001; ... . В этих случаях модуль разности \х — 5\ стремится к нулю: \х—5|= =0,1; 0,01; 0,001; ....

Число 5 в приведенном примере называют пределом пере­менной величины х и пишут

Определение 1. Постоянная величина а называется

пределом переменной х, если модуль разности при

изменении х становится и остается меньше любого как

угодно малого положительного числа е.

Итак, (предел х равен а) или (х стремится

к а).

182

2. Основные свойства пределов

1. Предел алгебраической суммы конечного числа переменных величин равен алгебраической сумме пределов слагаемых:

2. Предел произведения конечного числа переменных величин равен произведению их пределов:

3. Постоянный множитель можно выносить за знак предела:

Например,

4. Предел отношения двух переменных величин равен отно­шению пределов, если предел знаменателя не равен нулю:

6. Предел целой положительной степени переменной величины Равен той же степени предела этой же переменной:

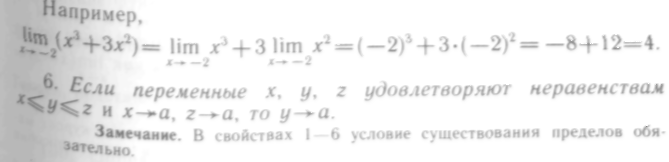
183

3. Предел функции в точке

Выше мы рассматривали независимые переменные величины, каждая из которых стремится к своему пределу независимо от другой.

Пусть теперь даны две переменные величины х и у, связан функциональной зависимостью . Рассмотрим вопрос о пре-

деле функции при условии, что задан предел ее аргумента

Если при х, стремящемся к а, функция стремится к b,

говорят, что предел функции в точке х=а равен b и пишут

.

Отметим, что во всем дальнейшем изложении, где говорится пределе функции в точке а, будем предполагать, что функция определена в некоторой окрестности точки а. В самой же точке а функция может быть не определена.

Однако такой метод нахождения предела очень громоздок, поэтому на практике он не применяется. Упростить решения за­дач на вычисление пределов функций позволяют основные свой­ства пределов, перечисленные выше.

94. Найти

Решение. Используя последовательно свойства 1, 3 и 5 предела, получим

* Более строгое определение предела функции дастся в полных курсах математического анализа. Ввиду сложности этого определении в данном пособии оно не приводится.

184

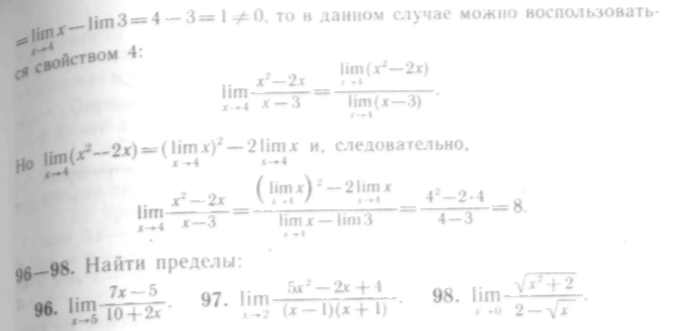
4. Приращение аргумента и приращение функции

Если аргумент функции изменяется от значения х до нового значения х_н, то разность этих значений называют приращением аргумента и обозначают символом (читается: «дельта икс»). Следовательно, , откуда .

Сама функция при таком изменении аргумента принимает новое значение ,т. е. получим приращение функции

Геометрически приращение аргумента изображается прира­щением абсциссы точки кривой, а приращение функции - прира­щением ординаты этой точки (рис. 90).

99. Найти приращении аргумента и функции , если аргумент х изменяется от 1 до 1,02.

4⁰. Вычитай из нового первоначальное значение функции, найдем приращение функции: .

К тому же результату можно прийти иначе. Сначала найдем приращение данной функции в общем виде.

Теперь, подставляя сюда значения х и , получим

100. Определить приращения аргумента и функции , аргумент х изменяется от 2 до 2,5.

185