- •Глава IV
- •§ 1. Свойства и графики основных элементарных функций
- •1. Постоянные и переменные величины
- •2. Область изменения переменной
- •3. Определение функции. Частное значение функции
- •4. Область определения функции
- •5. Способы задания функции
- •6. Основные свойства функций
- •7. Основные элементарные функции
- •§ 2. Предел и непрерывность функции
- •1. Предел переменной величины
- •2. Основные свойства пределов
- •3. Предел функции в точке
- •4. Приращение аргумента и приращение функции
- •5. Понятие о непрерывности функции
- •8. Вычисление пределов
- •§ 3. Производная
- •1. Задачи, приводящие к понятию производной
- •2. Определение производной
- •3. Общее правило нахождения производной
- •4. Частное значение производной
- •5. Связь между непрерывностью и дифференцируемостью функции
- •§ 4. Правила и формулы дифференцирования элементарных функций
- •1. Таблица правил и формул дифференцирования
- •2. Правила дифференцирования алгебраической суммы, произведения и частного
- •3 Правило дифференцирования сложной функции
- •4. Дифференцирование логарифмических функций
- •5. Производная степенной функции
- •6. Производная показательной функции
- •7. Дифференцирование тригонометрических функций
- •327. Найти
- •8. Дифференцирование обратных тригонометрических функций
- •358. Дано: Решение.
- •§ 5. Геометрический и механический смысл производной
- •1. Геометрический смысл производной
- •2. Механический смысл производной
- •3. Производная второго порядка и ее механический
- •4. Приложения производной к решению физических задач
- •§6. Дифференциал
- •1. Понятие дифференциала
- •2. Геометрический смысл дифференциала
- •3. Вычисление дифференциала
- •4. Дифференциал сложной функции
- •5. Применение дифференциала в приближенных вычислениях
- •§ 7. Исследование функций и построение графиков
- •1. Возрастание и убывание функций
- •2. Исследование функции на экстремум с помощью первой производной
- •3. Исследование функции на экстремум с помощью второй производной
- •4. Наибольшее и наименьшее значения функции
- •5. Практическое применение производной
- •6. Вогнутость и выпуклость. Точки перегиба
- •7. Построение графиков функций
7. Основные элементарные функции
Основные элементарные функции подробно изучались в школе. Напомним кратко основные свойства некоторых из них.
1 Линейная
функция
![]() —
действительные
—
действительные
числа. Область определения множество всех действительных
чисел! Графиком линейной функции является прямая (рис. 82).
Если 6 = 0, то
![]() ;
эта функция выражает прямую
про-порциональную зависимость между х
и у.
В этом случае
прямая проходит через начало
координат (рис.
83).
;
эта функция выражает прямую
про-порциональную зависимость между х
и у.
В этом случае
прямая проходит через начало
координат (рис.
83).
Угловой коэффициент
k
равен
![]() ,
где—
,
где—![]() угол,
образован-
угол,
образован-
ный прямой с положительным направлением оси абсцисс.
Функция возрастает,
если k>0
(угол
![]() —
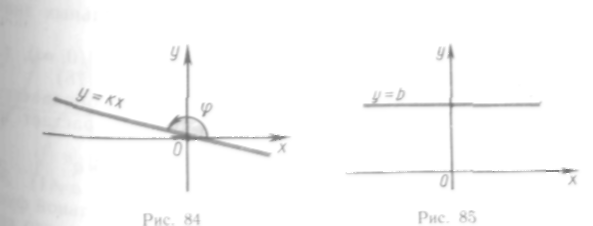
острый; рис. 83); функция убывает, если
k<0
(угол
—
острый; рис. 83); функция убывает, если
k<0
(угол
![]() тупой;
рис. 84).
тупой;
рис. 84).
При k = Q получаем постоянную функцию y=b (рис. 85); в частности, если k = 0 и b = 0, то у = 0 (ось абсцисс).
Рассмотрим вопрос о четности и нечетности линейной функции.
Если k
= 0, то
![]() ,
т. е. в этом случае функция
,
т. е. в этом случае функция
четная.
Если 6 = 0, то
![]() ,
т. е. в этом случае функция нечетная.
,
т. е. в этом случае функция нечетная.
Если
k![]() 0,
b
0
то
0,
b
0
то![]() ,
т. е. в этом
,
т. е. в этом
случае функция не является ни четной, ни нечетной.
2. Степенная
функция![]() ,
где п
— любое
действительное
,
где п
— любое
действительное
число.
179

При n = 3 получим функцию у=х3, графиком которой является кубическая парабола (см. рис. 74).
Отметим некоторые
свойства функции
![]()
Область определения
—- множество всех действительных
сел.
Функция
нечетная, так как
![]() .
Функция возрастает во всей области
определения.
.
Функция возрастает во всей области
определения.
Степенная функция
![]() в случае,
когда п —
четное число
в случае,
когда п —
четное число
обладает теми же
свойствами, что и функция![]() ,
а в случае,
,
а в случае,
когда п
— нечетное
число, — теми же свойствами, что и
функция
![]()
При п=1
получим
функцию![]() которая
выражает обратную пропорциональную
зависимость между х
и у.
Графиком
функции является гипербола (рис. 86).
которая
выражает обратную пропорциональную
зависимость между х
и у.
Графиком
функции является гипербола (рис. 86).
Отметим некоторые
свойства функции
![]() .
.
Область определения
- множество всех действительных
чисел, кроме x
= 0. Функция нечетная, так как![]()
![]() . Функция убывает
при
. Функция убывает
при
![]() и
при
и
при
![]()
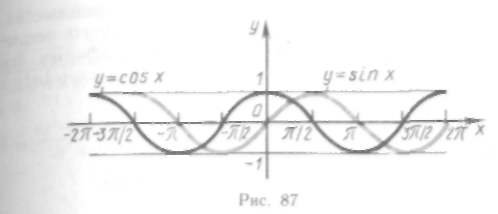
3. Показательная функция у = ах, где основание степени a — данное положительное число, не равное единице, а показатель степени х — переменная величина, которая может принимать любые действительные значения.
Основание степени
а считается
отличным от единицы, так как а= 1 степень
1х
при всяком значении х
равна 1. т.е.
функция
![]() становится
не зависящей от х.
Кроме того,
предполагается а>0, поскольку при
а<0 для ряда значений х
функция не
существует. Например, при а=-9
и х=1/2 имели
бы ах
= (—9)1/2
=
становится
не зависящей от х.
Кроме того,
предполагается а>0, поскольку при
а<0 для ряда значений х
функция не
существует. Например, при а=-9
и х=1/2 имели
бы ах
= (—9)1/2
=
![]() ,
а это есть мнимое выражение.
,
а это есть мнимое выражение.
Функция у
= ах
определена
для всех действительных знаний, т.е.
![]()
Областью изменения
функции служит интервал
![]() график находится в верхней полуплоскости
(см. рис. 78).
график находится в верхней полуплоскости
(см. рис. 78).
Свойствами четности и нечетности функция не обладает
Функция
![]() является
монотонной; она возрастает при а>1
и убывает при 0<а<1.
является
монотонной; она возрастает при а>1
и убывает при 0<а<1.
График проходит
через точку (0; 1), так как
![]()
4. Логарифмическая
функция
![]()
![]() .Эта
функция
является обратной по отношению к
показательной функ-
ции, так как если
.Эта
функция
является обратной по отношению к
показательной функ-
ции, так как если
![]() ,
то
,
то
![]() .
Отсюда следует, что
.
Отсюда следует, что
180
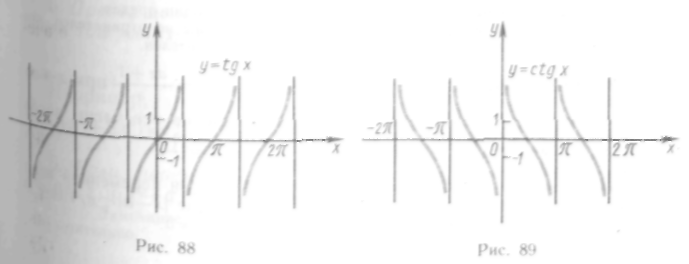
фик логарифмической функции симметричен графику показательной функции относительно биссектрисы I и III координатных углов (см. рис. 78).
Область определения
логарифмической функции — множество
всех положительных чисел, т. е.
![]() (отрицательные
числа и нуль логарифмов не имеют).
(отрицательные
числа и нуль логарифмов не имеют).
Область значений функции — множество всех действительных чисел.
Свойствами четности и нечетности функция не обладает.

181