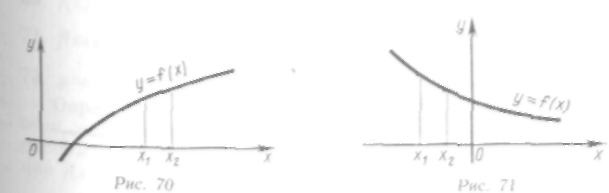
6. Основные свойства функций

Определение 4. Функция называется возраста-

ющей на некотором интервале, если для любых х из этого интервала большему значению аргумента соответствует большее значение функции, т. е. при имеет место

неравенство (рис. 70).

Функция называется убывающей на некотором

интервале, если тля любых х из этого интервала большему значению аргумента соответствует меньшее значение функции, т. е. при имеет место неравенство

(рис. 71).

Если же для любых значений х, взятых из некоторого промежутка и удовлетворяющих условию вытекает нестрогое

173

Функция называется кусочно-монотонной в данном

промежутке, если этот промежуток можно разбить на конечное число промежутков, в каждом из которых функция монотонна.

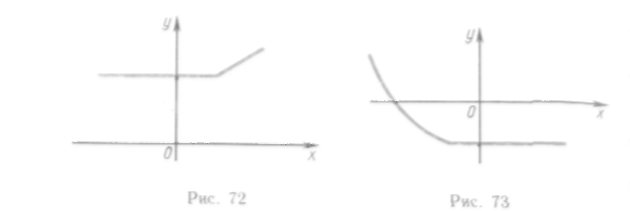
Например, функция определена в интервале

и является кусочно-монотонной на нем, так как в промежутке она убывает, а в промежутке (0, ) возрастает (рис. 76). Функция определена в интервале _. Эта функция не является кусочно-монотонной, так как интервал нельзя разбить на конечное число таких промежутков, в каждом из которых функция была бы монотонной.

174

т.е. данная функция является нечетной.

62. Выяснить, является ли функция четной или нечетной.

175

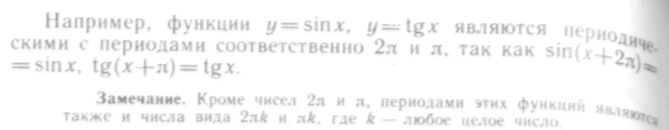
75. Доказать, что функция являются периодическими с периодом _.

Решение. Так к то

период функции равен

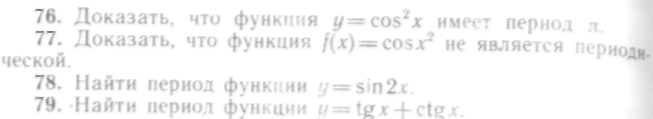
Определение 7. Пусть функция определена на

отрезке [а, b] и является монотонной, а область изменения функции у есть отрезок (рис. 77). Каждому значению y_о из отрезка будет соответствовать одно значение Х₀ из отрезка [а, b] такое, что . Следовательно, на отрезке [а, b] определена функция . Эта функция называется обратной для функции и, наоборот, функция является обратной для функции . Поэтому их называют взаимно обратными.

Графиками функций служит одна и та же

линия, так как эти функции выражают одну и ту же функцио­нальную зависимость между переменными х и у.

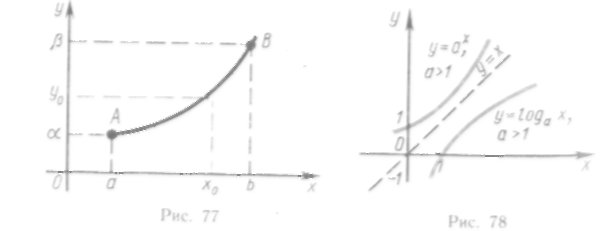
Примерами взаимно обратных функций являются функции _, где или функции и , где .

Построение их графиков отличается лишь тем, что значения независимой переменной для функции откладывают на

176

177

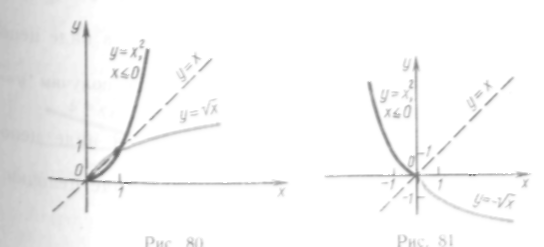
Если рассматривать функцию на полуинтервале [о, ] то

и каждому значению соответствует только одно значение х. В этом случае обратная функция существует и определяется уравнением (рис. 80).

Легко убедиться в том, что функция на полуинтервале (- ; 0] также имеет обратную функцию. Действительно, в этом случае каждому значению соответствует единственное значение х и обратная функция определяется уравнением (Рис.81)

Например, функция является сложной функцией, так как ее можно представить в виде , где u= х²+5х. Функция , также есть сложная функция;

ее можно представить в виде , где _.

Сложная функция может содержать несколько промежуточ­ных переменных. Например, если _, где , то сложная функция содержит две промежуточные пере­менные.

178