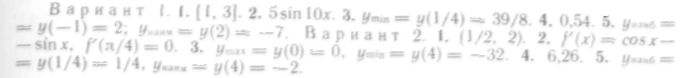6. Вогнутость и выпуклость. Точки перегиба

Чтобы исследовать более подробно особенности поведения функции, введем понятия вогнутости и выпуклости и точек пере­гиба графика функции. Рассмотрим кривые, изображенные на рис. 125.

Будем предполагать, что линия, заданная уравнением имеет в точке касательную, не параллельную оси ординат.

Кривая выпукла (соответственно вогнута) в некотором про­межутке, если она выпукла (вогнута) во всех точках этого про­межутка.

Промежутки выпуклости и вогнутости кривой можно нахо­дить с помощью производной.

274

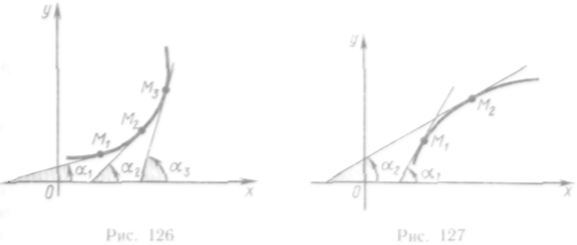
— возрастающая функция. Следова­тельно, проведя касательные к графику функции в точках Mi, М2, ... (рис. 126), получим, что тангенсы углов растут

вместе с ростом х: , т. е. функция возрас-

тает, поэтому ее производная положительна. А это озна-

чает, что графиком функции f(x) является вогнутая кривая.

Аналогично можно показать, что из условия в неко-

тором промежутке следует выпуклость кривой в этом промежутке (рис. 127).

Для нахождения интервалов выпуклости графика функции используют следующее правило:

275

Как мы уже отмечали, иногда кривая в одной своей части выпукла, а в другой вогнута; так, например, часть синусоиды (рис. 128) выпукла выше оси Ох и вогнута ниже оси Ох, причем точка А служит границей между ними. Касательная, проведенная к кривой в этой точке, является общей для ее выпуклой и вогну­той части; эта касательная в то же время пересекает кривую в точке касания; поэтому синусоида в точке А ни выпукла, ни вогнута. Эта точка носит название точки перегиба.

Точкой перегиба кривой называется такая точка, которая отделяет выпуклую часть кривой от вогнутой.

Доказательство. Пусть, например, в точке х₀ и знак меняет с плюса на минус. Это означает, что слева от хц кривая вогнута, а справа - выпукла, т. е. точка хо отде­ляет область вогнутости от выпуклости и является точкой пере­гиба.

Из признака существования точки перегиба следует правило ее нахождения:

276

637. Исследовать на выпуклость, вогнутость и точки перегиба кривую

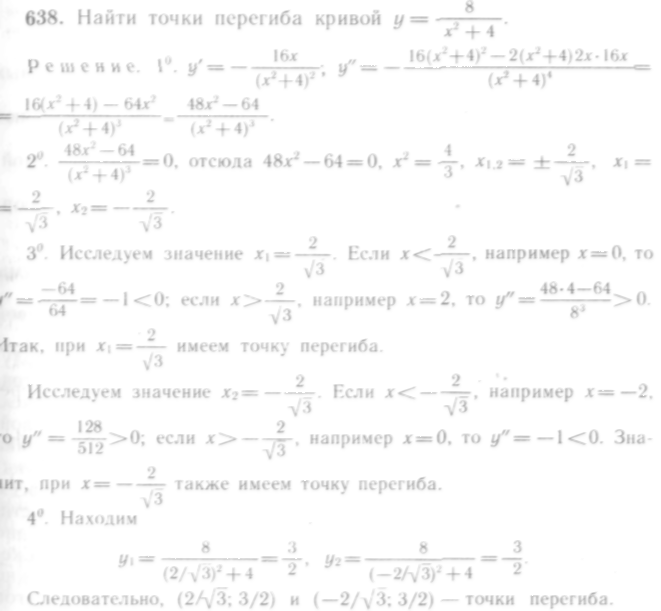
277

639. Исследовать функцию на максимум, минимум и точку перегиба.

Решение. Найдем первую и вторую производные:

640—643. Исследовать на вогнутость, выпуклость и точки пере­гиба функции:

7. Построение графиков функций

При построении графиков функций с помощью производных полезно придерживаться такого плана:

1°. Находят область определения функции и определяют точки разрыва, если они имеются.

2°. Выясняют, не является ли функция четной или нечетной; проверяют ее на периодичность.

3°. Определяют точки пересечения графика функции с коор­динатными осями, если это возможно.

4°. Находят критические точки функции.

5°. Определяют промежутки монотонности и экстремумы функции.

6°. Определяют промежутки вогнутости и выпуклости кривой и находят точки перегиба.

7°. Используя результаты исследования, соединяют полу­ченные точки плавной кривой. Иногда для большей точ­ности графика находят несколько дополнительных точек; их координаты вычисляют, пользуясь уравнением кривой. Этот план исследования функции и построения ее графика является примерным, его не всегда надо придерживаться пунк­туально: можно менять порядок пунктов, некоторые совсем опускать, если они не подходят к данной функции. В частности, если нахождение точек пересечения с осями координат связано с большими трудностями, то это можно не делать; если выраже­ние для второй производной окажется очень сложным, то можно ограничиться построением графика на основании результатов

278

исследования первой производной; если функция четная, то ее график симметричен относительно оси Оу, поэтому достаточно построить график для положительных значений аргумента, при­надлежащих области определения функции, и т, п.

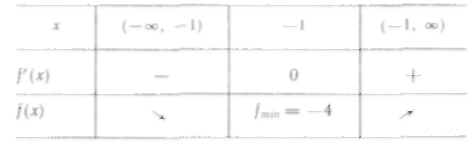
Составим таблицу:

279

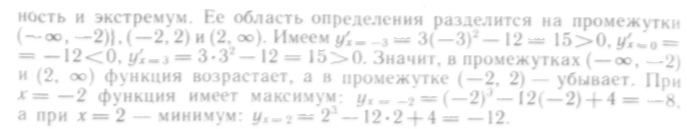
Составим таблицу:

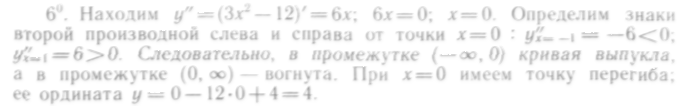
Составим таблицу:

280

Составим таблицу:

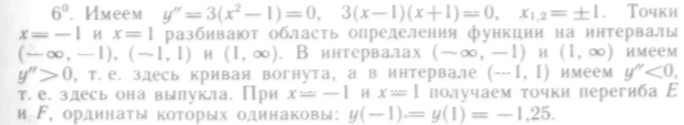
Составим таблицу:

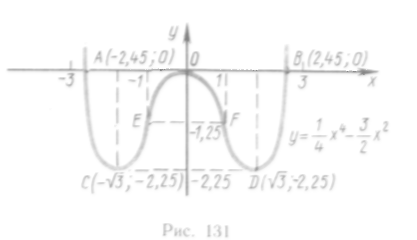
7°. График изображен на рис. 131.

281

Составим таблицу:

6°. Находим

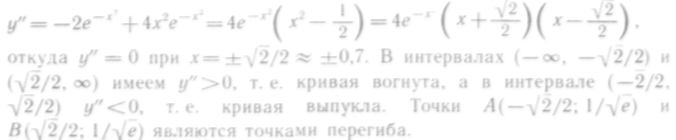
Составим таблицу:

282

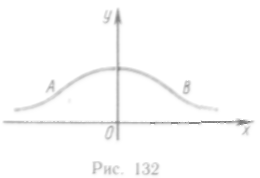
Составим таблицу:

6°. Находим

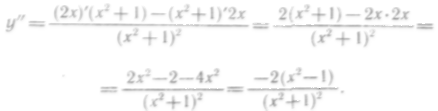
283

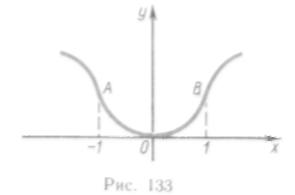
Составим таблицу:

7⁰. График изображен на рис. 133.

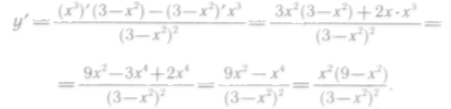
284

6°. Находим

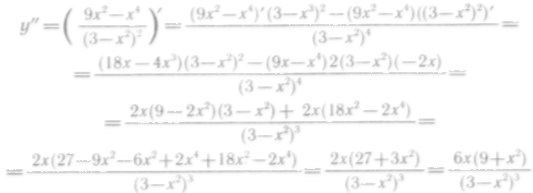
Очевидно, что только при ; кроме того, не существует при (напомним, что мы рассматриваем значения) _.

В интервале имеем , т. е. кривая вогнута, а в интервале имеем , т. е. кривая выпукла.

Вследствие симметрии графика относительно начала координат заключаем, что в интервале и в интервале _. Это означает, что (0, 0) точка перегиба.

7". График изображен на рис. 134.

650.

285

6°. Построим график, не исследуя вогнутости и выпуклости кривой. Из рис. 135 видно, что в каждом из исследуемых интервалов имеется точка перегиба. Вычислив у" и приравняв ее нулю, можно определить точное положение этих точек.

286

Вопросы и задачи для конспектирования

287

Ответы

Контрольное задание

Вариант 1

288

Вариант 2

Ответы