3. Исследование функции на экстремум с помощью второй производной

Часто бывает рациональнее исследовать функцию на экстре­мум с помощью второй производной. Рассмотрим сущность этого метода.

Знак первой производной данной функции характеризует возрастание и убывание функции. Точно так же знак второй про­изводной связан с возрастанием и убыванием первой производ­ной.

Если первая производная в некотором интервале дифферен­цируема и возрастает, то в каждой точке этого интервала вторая производная положительна; если же первая производная убы­вает, то вторая производная в каждой точке этого интервала отрицательна.

Теперь выясним, как изменяется первая производная в точ­ках экстремума и близких к ним точках с увеличением аргу­мента. Первая производная при переходе через точку максимума меняет знак с плюса на минус; иными словами, она от положи­тельных значений переходит через нуль к отрицательным, т. е. убывает, а значит, ее производная должна быть отрицательна. Итак, в точке максимума данной функции первая производная равна нулю, а вторая производная отрицательна.

Аналогично можно показать, что в точке минимума функции первая производная равна нулю, а вторая положительна.

265

Отсюда вытекает правило исследования функции на экстре­мум с помощью второй производной:

5 82—599. Исследовать на экстремум с помощью второй произ­водной следующие функции:

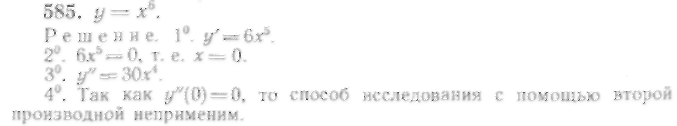
266

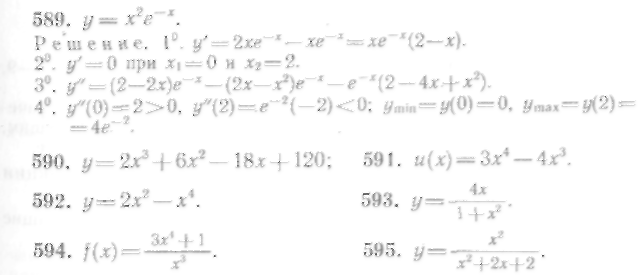
267

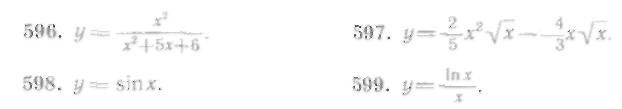
4. Наибольшее и наименьшее значения функции

Пусть функция непрерывна на отрезке [а, Ь]. В этом случае, как известно, она принимает как наибольшее, так и наи­меньшее значения на этом отрезке. Во многих прикладных вопро­сах бывает важно найти те точки отрезка [а, Ь], которым отве­чают наибольшее и наименьшее значения функции.

При решении этой задачи возможны два случая:

1. либо наибольшее (наименьшее) значение функции дости­гается внутри отрезка и тогда эти значения окажутся в числе экстремумов функции;

2. либо наибольшее (наименьшее) значение достигается на концах отрезка [а, Ь].

Итак, чтобы найти наибольшее и наименьшее значения непре­рывной на отрезке [а, Ь] функции , нужно:

600. Найти наибольшее и наименьшее значения функции

Вычислим значения функции в критических точках:

601. Найти наибольшее и наименьшее значения функции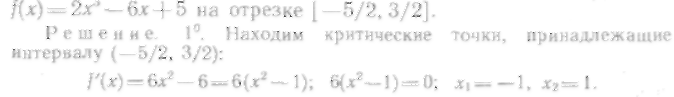

268

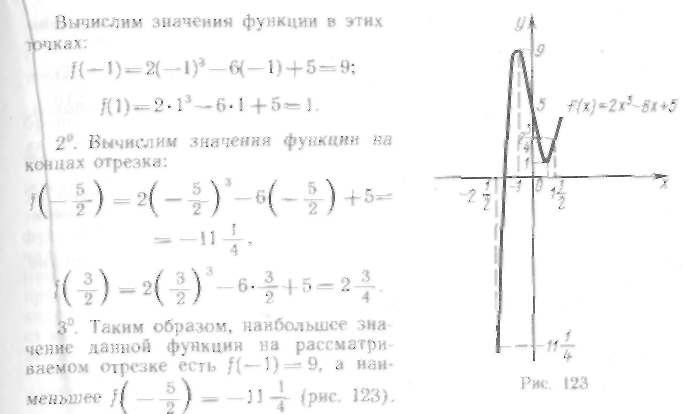
602. Найти наибольшее и наименьшее значения функции на отрезке [ — 1,2].

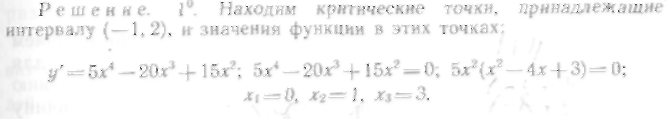
Критическая точка не принадлежит заданному отрезку.

Вычисляем значения функции в двух других критических точках:

603. Найти наибольшее и наименьшее значения функции на отрезке [—6, 8].

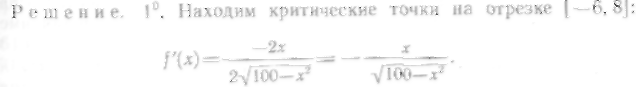
На рассматриваемом отрезке имеем только одну критическую точку х=0; при этом

269

604—609. Найти наибольшее значение М и наименьшее значение m следующих функций на указанных отрезках:

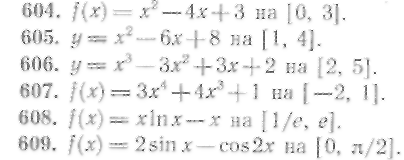
5. Практическое применение производной

Рассмотрим задачи, связанные с практическим применением производной. При их решении не дается готовой функции для исследования, а ее нужно составить самостоятельно по условию задачи. При этом сначала следует установить, какую величину выбрать за независимую переменную. В задачах, где выбор мо­жет быть сделан не единственным образом, следует остановиться на таком выборе, при котором исследуемая функция оказыва­ется более простой.

610. Разложить число 100 на два слагаемых так, чтобы их произведение было наибольшим.

270

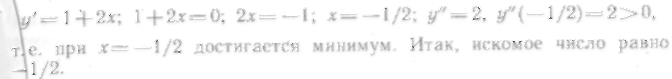
612. Путь s, пройденный за время t материальной точкой, брошенной вертикально вверх с начальной скоростью v_o, выра­жается формулой , где g — ускорение силы тя­жести. Определить высоту наибольшего подъема точки.

613. Требуется вырыть силосную яму объемом 32 м³, имею­щую квадратное дно, так чтобы на облицовку ее дна и стен пошло наименьшее количество материала. Каковы должны быть размеры ямы?

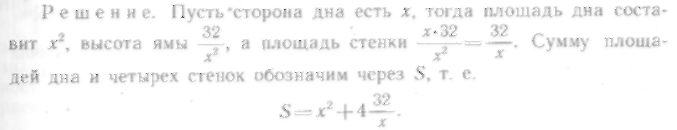
Найдем производную S по х:

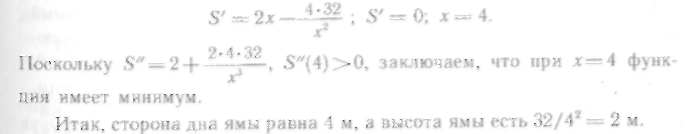
614. Имеется квадратный лист жести, сторона которого

. Вырезая по всем его углам равные квадраты и загибая оставшуюся часть, нужно изготовить коробку (без крышки). Каковы должны быть размеры вырезаемых квадратов, чтобы коробка имела наибольший объем?

271

Найдем значение х, при котором функция примет наибольшее значение. Для этого сначала преобразуем функцию, а затем исследуем ее на экстремум:

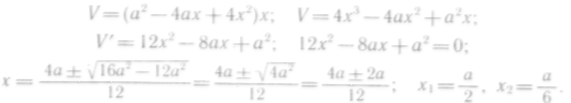
Очевидно, что значение не отвечает условию, так как в этом случае квадрат был бы разрезан на четыре равные части и никакой коробки не получилось бы. Поэтому исследуем функцию на экстремум в критической очке

т.е. при достигается максимум. Итак, сторона вырезаемого

квадрата должна быть равна . В данном конкретном случае

при а = 60см получим

615. Из круглого бревна радиуса R требуется вырезать прямоугольную балку максимальной прочности. Известно, что прочность балки прямо пропорциональна произведению се ширины на квадрат высоты. Какими должны быть размеры балки, чтобы ее прочность была максимальной?

Находим производную и приравниваем ее нулю:

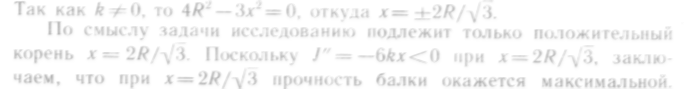
616. Оросительный канал имеет форму равнобочной трапеции, боковые стороны которой равны меньшему основанию. При ка­ком угле наклона боковых сторон площадь сечения канала явля­ется наибольшей?

272

Приравняем производную нулю и решим полученное уравнение:

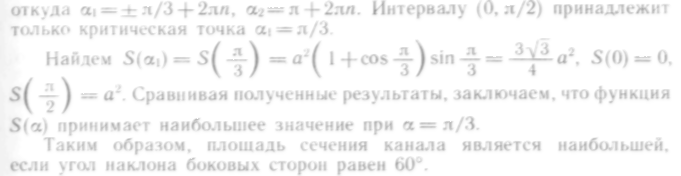
617. Суточные расходы при плавании судна состоят из двух частей: постоянной, равной а руб.. и переменной, возрастающей пропорционально кубу скорости. При какой скорости и плава­ние судна окажется наиболее экономичным?

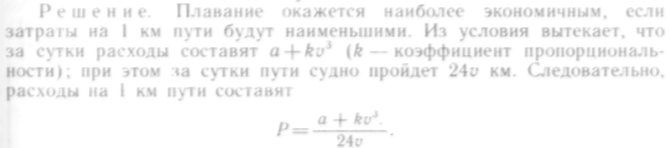
функция при v = 0 имеет бесконечный разрыв, но нулевая скорость для нас не представляет интереса.

618. Разложить число а на два слагаемых так, чтобы их произведение было наибольшим.

619. Найти такое число, чтобы разность между этим числом и его квадратом была наибольшей.

620. Найти такое число, чтобы разность между этим числом и квадратным корнем из него была наименьшей.

621. Окно имеет форму прямоугольника, завершенного полу­ кругом. Периметр окна равен а. Каковы должны быть размеры окна, чтобы оно пропускало наибольшее количество света?

273

622. Тело движется по закону 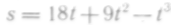. Найти его максимальную скорость.

623. Количество Q вещества, получающегося в процессе химической реакции, выражается формулой 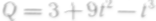, где t — время. Найти максимальную скорость реакции.

624. Прилегающую к дому прямоугольную площадку нужно оградить решеткой длиной 120 м. Определить размеры площадки, так чтобы она имела наибольшую площадь.

625. Определить размеры открытого бассейна объемом 256 м³, имеющего квадратное дно, так чтобы на облицовку его стен и дна было израсходовано наименьшее количество материала.

626. Какой из равнобедренных треугольников с заданным периметром 2р имеет наибольшую площадь?

627. Найти отношение высоты к диаметру конуса, имеющего при заданном объеме наименьшую боковую поверхность.

628. Из всех цилиндров с площадью полной поверхности найти тот, который имеет наибольший объем.