2. Исследование функции на экстремум с помощью первой производной

На рис. 116. изображен график функции . Рассмотрим окрестность точки х = О, т.е. некоторый интервал, со­держащий эту точку. Как видно из рисунка, существует такая окрестность точки х=0, что наибольшее значение функции в этой окрестности принимается в точке х= 0. Например, на интервале (— 1, 1) наибольшее значение, равное нулю, функ­ция принимает в точке х = 0. Точку х = 0 называют точкой максимума* этой функции.

Аналогично, точку х = 2 называют точкой минимума** функ­ции , так как значение функции в этой точке меньше, чем ее значение в остальных точках некоторой окрестности точки х = 2.

260

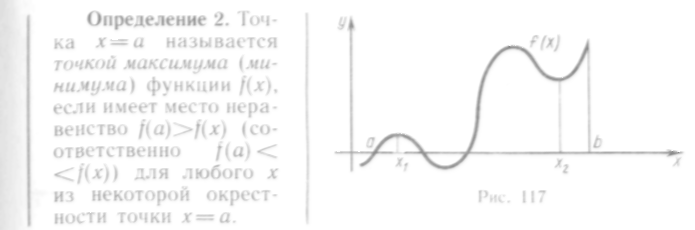
Если — точка максимума (минимума) функции, то говорят, что имеет максимум (минимум) в точке

Максимум и минимум функции объединяют названием экстре­мум функции, а точки максимума и минимума называют точ­ками экстремума (экстремальными тачками).

Не следует считать, что май пункции является наибольшим значением во всей области определения этой функции; он является наибольшим лишь по сравнению со значениями функ­ции, взятыми в некоторой окрестности точки максимума.

На данном интервале функция может иметь несколько макси­мумов и несколько минимумов, причем некоторые из максимумов могут быть меньше некоторых минимумов.

Из рис. 117 видно, что значение , представляющее собой максимум функции , не является наибольшим значением этой функции на интервале (а, Ь) и, более того, меньше, чем значение , являющееся минимумом данной функции.

Аналогично, минимум функции не обязательно является наи­меньшим значением данной функции.

Определим, при каких условиях функция имеет максимум или минимум.

А Теорема 3 (необходимый признак экстремума). Если х — а является точкой экстремума функции, и производная в этой точке существует, то она равна нулю:

Доказательство. Производная функции в точке х=а не может быть отличной от нуля, так как в случае функция возрастала бы в некотором интервале, содержащем точку а', а в случае убывала бы в некотором интервале, содержащем точку а; другими словами, при и функция не имеет экстремума в точке о, что противоречит условию. Значит

Геометрически необходимый признак экстремума означает, что если — точка экстремума функции , то касательная (в том случае, когда она существует) к графику этой функ­ции в точке параллельна оси Ох (рис. 118).

Легко убедиться в том, что необходимое условие экстремума функции не является достаточным, т. е. из того факта, что вовсе не следует, что функция имеет экстремум при х = а.

Например, для функции, изображенной на рис. 119, касательная

261

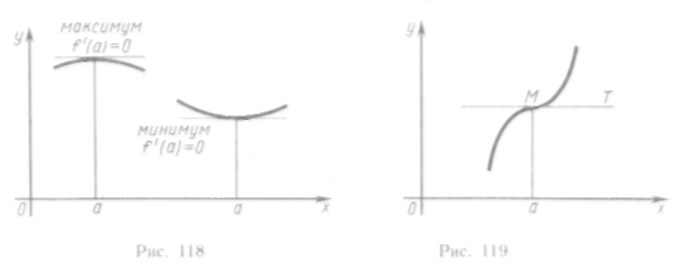
МТ параллельна оси Ох, т. е. , однако экстремума в этой точке функция не имеет.

Таким образом, обращение первой производной в нуль является необходимым, но не достаточным условием экстре­мума.

Доказательство. Пусть при переходе х через а произ­водная меняет знак с плюса на минус. Тогда слева от а произ­водная положительна и, следовательно, здесь находится интер­вал возрастания функции. Справа же от а производная отрица­тельна, и поэтому здесь находится интервал убывания функции. Точка отделяющая интервал возрастания функции от интервала убывания, есть точка максимума.

Аналогично доказывается, что если при переходе х через а производная меняет знак с минуса на плюс, то а является точкой минимума.

Для функции, изображенной на рис. 119, при переходе через критическую точку производная не меняет знак и в этой точке нет экстремума.

Таким образом, исследование производной позволяет во многом изучить поведение функции . При этом нужно понимать, что в своих рассуждениях мы с помощью известного графика функции находили значения производной на тех или иных участках кривой. На практике же, конечно, посту­пают наоборот: рассматривают производную некоторой функции и с ее помощью исследуют характер функции.

Нетрудно выделить основные моменты этого исследования.

262

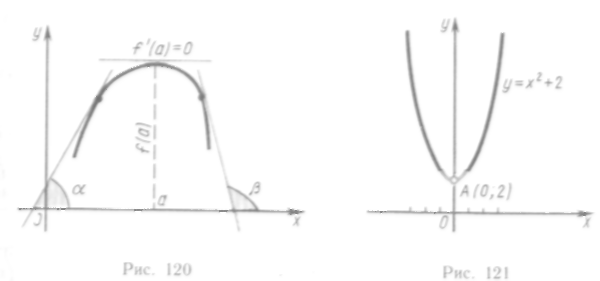
564—580. Исследовать на экстремум следующие функции:

263

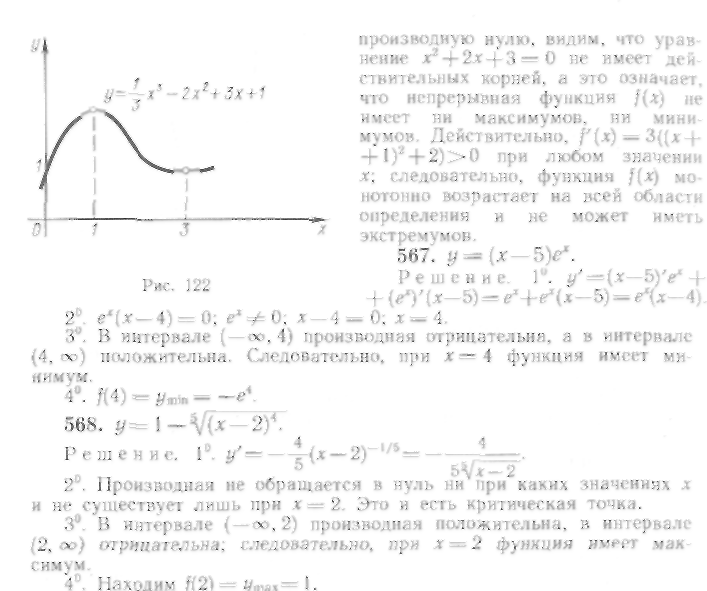
569. ;

Для оформления записи исследования функции можно поль­зоваться таблицей, в первой строке которой записаны интер­валы знакопостоянства производной и критические точки функ­ции; во второй — знаки первой производной в этих интервалах и ее значения в критических точках; в третьей — поведение функ­ции в этих интервалах и ее значения в критических точках.

2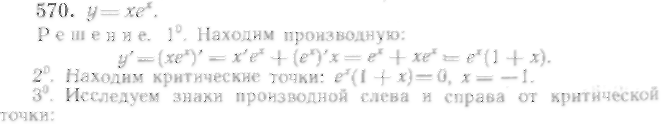 64

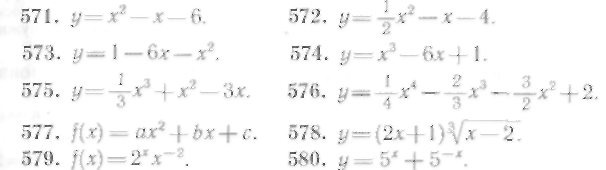
581. Может ли точка экстремума функции быть одновременно и точкой экстремума ее производной?