- •Глава IV
- •§ 1. Свойства и графики основных элементарных функций
- •1. Постоянные и переменные величины
- •2. Область изменения переменной
- •3. Определение функции. Частное значение функции
- •4. Область определения функции
- •5. Способы задания функции
- •6. Основные свойства функций
- •7. Основные элементарные функции
- •§ 2. Предел и непрерывность функции
- •1. Предел переменной величины
- •2. Основные свойства пределов
- •3. Предел функции в точке
- •4. Приращение аргумента и приращение функции
- •5. Понятие о непрерывности функции
- •8. Вычисление пределов
- •§ 3. Производная
- •1. Задачи, приводящие к понятию производной
- •2. Определение производной
- •3. Общее правило нахождения производной
- •4. Частное значение производной
- •5. Связь между непрерывностью и дифференцируемостью функции
- •§ 4. Правила и формулы дифференцирования элементарных функций
- •1. Таблица правил и формул дифференцирования
- •2. Правила дифференцирования алгебраической суммы, произведения и частного
- •3 Правило дифференцирования сложной функции
- •4. Дифференцирование логарифмических функций
- •5. Производная степенной функции
- •6. Производная показательной функции
- •7. Дифференцирование тригонометрических функций
- •327. Найти
- •8. Дифференцирование обратных тригонометрических функций
- •358. Дано: Решение.
- •§ 5. Геометрический и механический смысл производной
- •1. Геометрический смысл производной
- •2. Механический смысл производной
- •3. Производная второго порядка и ее механический
- •4. Приложения производной к решению физических задач
- •§6. Дифференциал
- •1. Понятие дифференциала
- •2. Геометрический смысл дифференциала
- •3. Вычисление дифференциала
- •4. Дифференциал сложной функции
- •5. Применение дифференциала в приближенных вычислениях
- •§ 7. Исследование функций и построение графиков
- •1. Возрастание и убывание функций
- •2. Исследование функции на экстремум с помощью первой производной
- •3. Исследование функции на экстремум с помощью второй производной
- •4. Наибольшее и наименьшее значения функции
- •5. Практическое применение производной
- •6. Вогнутость и выпуклость. Точки перегиба
- •7. Построение графиков функций
§ 7. Исследование функций и построение графиков
1. Возрастание и убывание функций
2. Исследование функции на экстремум с помощью первой производной
3. Исследование функции с помощью второй производной
4. Наибольшее и наименьшее значения функции
5. Практическое применение производной
6. Вогнутость и выпуклость. Точки перегиба
7. Построение графиков функций
1. Возрастание и убывание функций
Понятие производной — одно из важнейших в математике. С помощью производной, учитывая ее механический смысл (скорость изменения некоторого процесса) и геометрический смысл (угловой коэффициент касательной), можно решать самые разнообразные задачи, относящиеся к любой области человеческой деятельности. В частности, с помощью производных стало возможным подробное исследование функций, что позволило очень точно строить их графики, находить их наибольшие и наименьшие значения и т. д.
Познакомимся с
основными идеями, связанными с
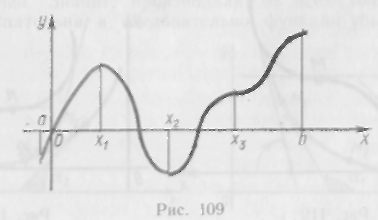
исследованием функций. Для этого
рассмотрим график какой-нибудь функции
![]() (рис. 109).
(рис. 109).
Интуитивно ясно,
что в интервалах
![]() данная
функция возрастает, а в интервале
данная
функция возрастает, а в интервале![]() —
убывает.
—
убывает.
255
В дальнейшем будем рассматривать только дифференцируемые функции.
Определение I.
Функция
![]() называется
возрастающей
в некотором
интервале, если в точках этого интервала
большему значению аргумента
соответствует бот шее значение
функции, и убывающей,
если
большему значению аргумента
соответствует меньшее значение
функции.
называется
возрастающей
в некотором
интервале, если в точках этого интервала
большему значению аргумента
соответствует бот шее значение
функции, и убывающей,
если
большему значению аргумента
соответствует меньшее значение
функции.

Тогда в обоих
случаях отношение приращения функции
к при ращению аргумента положительно,
т. е.
![]() .Далее,
поскольку функция
.Далее,
поскольку функция
![]() дифференцируема
на рассматриваемом интервале, то,
переходя к пределу при
дифференцируема
на рассматриваемом интервале, то,
переходя к пределу при
![]() ,
получим
,
получим
![]() ,
а это значит, что
,
а это значит, что![]()
Рассуждая
аналогично, можно показать, что в случае
убывания функции ее производная
отрицательна, т.е.
![]()
Все вышеизложенное
можно сформулировать как необходимый
прорастания (убывания) функции.
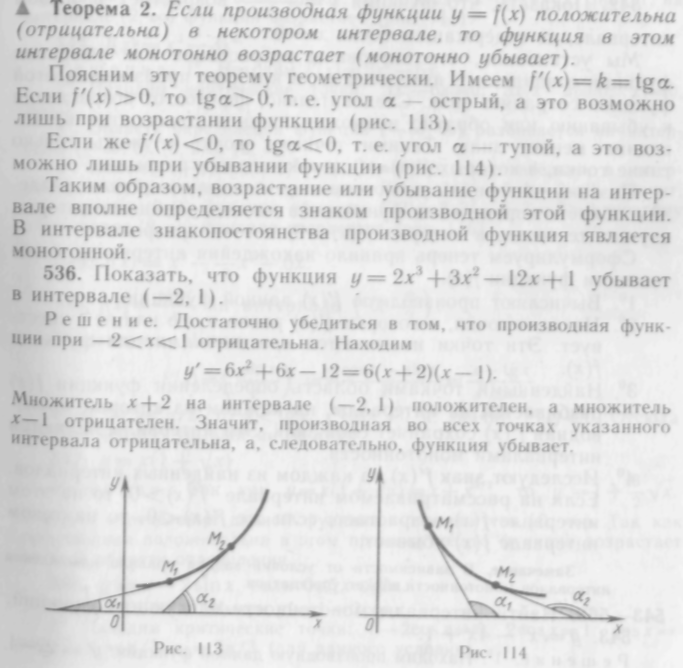
А
Теорема 1. Если
дифференцируемая функция
![]() _возрастает
(убывает) в данном интервале, то производная
этой
функции не отрицательна (не
положительна) в этом интервале.
_возрастает
(убывает) в данном интервале, то производная
этой
функции не отрицательна (не
положительна) в этом интервале.
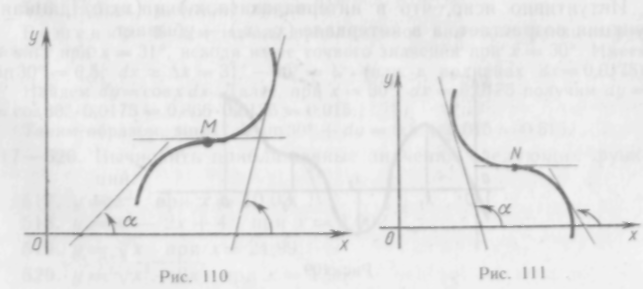
Геометрически утверждение теоремы означает, что касательные к графику возрастающей функции образуют острые углы о. с положительным направлением оси Ох или, быть может, в отдельных точках, вроде точки М (рис. 110), касательная парал-
256
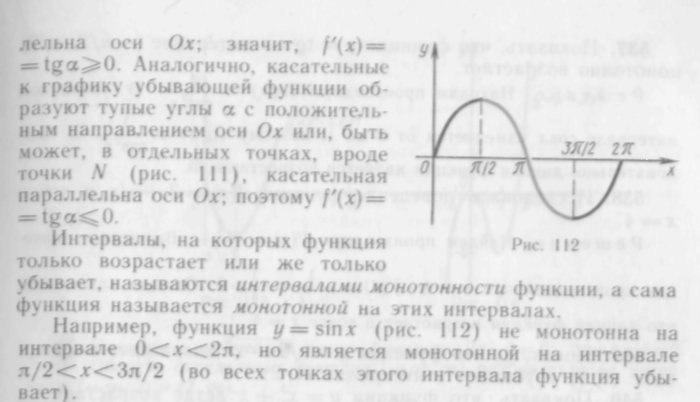
Обратное заключение также справедливо, оно выражается следующей теоремой.
9-1356 257
537. Показать, что
функция
![]() в интервале
в интервале
![]()
монотонно возрастают.

Мы установили, что
интервалы возрастания или убывания
функции совпадают с интервалами, в
которых производная этой функции
сохраняет знак. Следовательно, переход
от возрастания к убыванию или обратно
возможен лишь в точках, где производная
меняет знак. Такими точками могут служить
только такие точки, в которых
![]() ,
а также точки разрыва.
,
а также точки разрыва.
Поэтому интервалы
монотонности мы получим, если разделим
область определения функции на части,
границами которых служат те точки, в
которых
![]() ,
и точки разрыва.
,
и точки разрыва.
Сформулируем
теперь правило нахождения интервалов
монотонности следующих функции
![]() .
.

Замечание. 15. В зависимости от условий задачи правило нахождения интервалов монотонности может упрощаться.
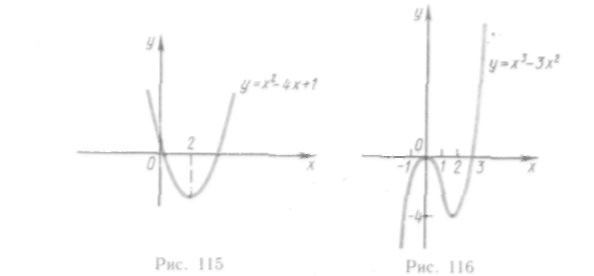
543—563. Найти интервалы монотонности следующих функций:
![]()
258



9* 259