§6. Дифференциал

• 1. Понятие дифференциала

• 2. Геометрический смысл дифференциала

• 3. Вычисление дифференциала

• 4. Дифференциал сложной функции

• 5.Применение дифференциала в приближенных вычислениях

1. Понятие дифференциала

Нахождение дифференциала функции, так же как и нахож­дение производной, является одной из основных задач дифферен­циального исчислений.

Умножив обе части этого равенства на , получим

Здесь у' есть функция от х и не зависит от ; следовательно. А входит в первое слагаемое в первой степени (т.е. линейно). Поэтому первое слагаемое представляет собой линейную часть приращении функции (про второе слагаемое этого сказать нельзя, поскольку также зависит от ).

Тогда при вторым слагаемым можно пренебречь, и первое слагаемое будет являться главной частью приращения функции (исключая случай, когда у' = 0).

245

Определение. Главная часть приращения функции, ли­нейная относительно приращения независимой перемен­ной, называется дифференциалом функции и обознача­ется знаком d, т. е.

Таким образом, для всякой функции производная у'

зависит только от одной переменной х, тогда как ее дифферен­циал зависит от двух независимых друг от друга переменных: х и

463. Найти приращение и дифференциал функции в точке

2. Геометрический смысл дифференциала

Рассмотрим график непрерывной функции (рис. 107).

Производная функции в точке с абсциссой х равна тангенсу угла наклона касательной к положительному направлению оси Ох, т. е.

246

находим ^то

Итак, дифференциал функции геометрически изображается приращением ординаты касательной, проведенной в точке М(х; у) при данных значениях х и

3. Вычисление дифференциала

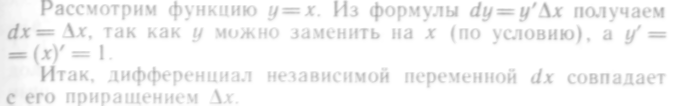
Учитывая это, дифференциал функции можно вычислить по формуле

(3)

Очевидно, чтобы вычислить дифференциал функции, нужно ее производную умножить на dх.

Отсюда следует, что правила нахождения дифференциала остаются теми же, что и для нахождения производных.

Для удобства пользования выпишем основные формулы на­хождения дифференциалов в виде таблицы:

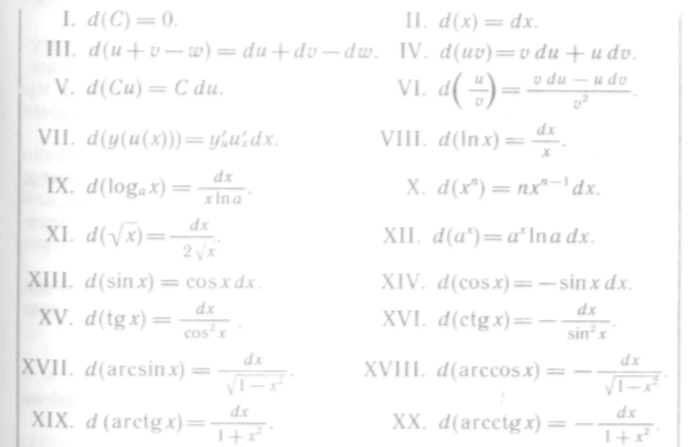
467. Найти дифференциалы функций:

247

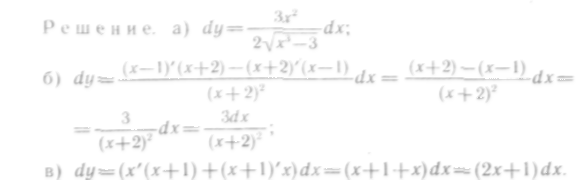
468—477. Найти дифференциалы функций:

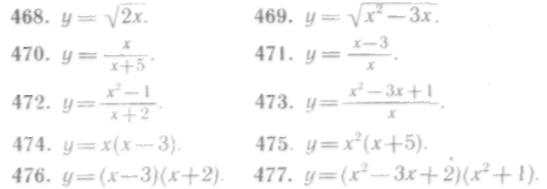
4. Дифференциал сложной функции

Выведем формулу дифференциала сложной функции. При этом мы, конечно, можем воспользоваться формулой производ­ной сложной функции. Однако сейчас мы убедимся в том, что нахождение дифференциала сложной функции имеет некоторые преимущества по сравнению с нахождением производной слож­ной функции.

Ранее было доказано, что в том случае, когда аргумент х является независимой переменной. Поэтому и при реше­нии предыдущих примеров, пользуясь формулой , мы вычисляли дифференциалы лишь для тех функций, для которых аргумент х есть независимая переменная.

Пусть теперь дана функция , которая косвенно зависит от х через другую зависимую переменную и (например, или ), т. е. — функция от функции или сложная функция. Очевидно, здесь х является независимой пере­менной, в то время как аргумент и (х) есть зависимая пере­менная.

Найдем дифференциал данной функции: Но согласно правилу производной сложной функции. Тогда

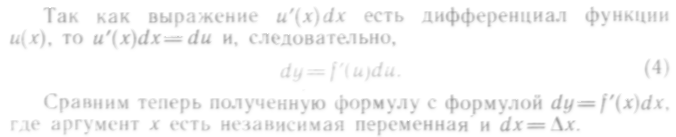
248

Хотя в формуле (4) аргумент и является зависимой перемен­ной и , но и в этом случае дифференциал функции равен произведению производной на дифференциал аргумента.

Это свойство дифференциала сохранять неизменной формулу вычисления по отношению к любому преобразованию аргумента называется инвариантностью дифференциала

Свойство инвариантности дифференциала позволяет вычисле­ние дифференциала производить более наглядно.

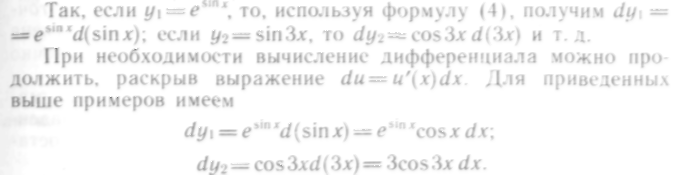
478—489. Найти дифференциалы функций: