4. Приложения производной к решению физических задач

Как известно, производная характеризует мгновенную ско­рость прямолинейного движения. Однако этим не исчерпывается использование производной. При изучении неравномерно ме­няющихся величин скорость их изменения всегда выражается с помощью производной.

Понятие скорости, заимствованное из физики, удобно при исследовании поведения любой функции. Какую бы зависимость

ни выражала функция , отношение есть средняя скорость изменения функции относительно изменения аргумента х, а —мгновенная скорость изменения функции

при некотором значении

444. Найти скорость изменения функции в произвольной точке.

445. Определить скорость изменения функции при

446. Доказать, что скорость изменения линейной функции постоянна.

447. Убедиться, что скорость изменения квадратичной функ­ции 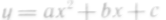выражается линейной функцией

448. Стороны и и Ь прямоугольника изменяются по закону

. С какой скоростью изменяется

его площадь S В момент времени ?

449. Основание параллелограмма и изменяется по за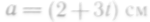кону , а высота h — по закону 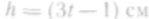. Опреде­лить скорость изменения его площади В момент

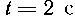
450. Убедиться, что скорость изменения логарифмической функции 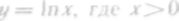, обратно пропорциональна х.

451.Убедиться, что скорость изменения показательной функ­ции , где, пропорциональна у.

452. Чему равна скорость изменения функций ? Вы­ числить ее значение для

Так как в практических приложениях нас обычно интересует не только сама функция, но и скорость ее изменения, то производная, будучи характеристикой скорости изменения функции,

242

имеет самые широкие практические применения в вопросах фи­зики, химии, геометрии и т.д. Приведем некоторые конкретные примеры использования понятия производной при определении скорости различных процессов.

1. Предположим, что в момент времени t масса еще не распавшеюся радиоактивного вещества была равна т, а через не­которое время, в момент , масса его уменьшилась (так как часть вещества превратилась в продукт распада) и стала равна (здесь отрицательно, поскольку масса радиоактивного вещества е течением времени уменьшается). Таким образом, за время масса имевшегося радиоактивного вещества изменилась на

Отношение представляет собой среднюю скорость распада за промежуток времени . Чем меньше этот промежуток, точнее указанное отношение выражает мгновенную скорость распада. Полому можно сказать, что мгновенная скорость рас­пада в момент времени t равна

2. Мгновенная мощность есть производная где — работа, совершаемая за время

3. Если V — объем жидкости, на который действует внешнее давление Р. то производная 1ает коэффициент сжатия жидкости при данном давлении.

4. Если твердое тело вращается вокруг оси, то угол поворота есть функция от времени t. Угловая скорость вращения в данный момент t численно равна производной

5. Сила тока есть производная , где — положительный электрический заряд, переносимый через сечение проводника за время

6. Теплоемкость при температуре Т есть производная

, где — количество теплоты, необходимое для изме­нения температуры на

453. Маховик за время t поворачивается на угол

(t— в секундах, в радианах). Определить угловую скорость, ) в конце 3-й секунды. Найти момент, когда прекратится вращение

454. Маховик, задерживаемый тормозом, за t с поворачивается

на угол _{(рад). Определить угловую скорость}

₂₄₃

маховика в момент времени и найти момент остановки вращения.

455. Количество электричества, протекающее через провод­ник, начиная с момента времени t = Q, задается формулой

. Найти силу тока в конце 6-й секунды.

Решение. Находим теплоемкость:

При получим

461. Закон изменения температуры Т тела в зависимости от времени t задан уравнением . С какой скоростью нагревается это тело в момент времени 10 с?

244