3. Производная второго порядка и ее механический

смысл

Производную от данной функции часто называют первой производной (или производной первого порядка). Очевидно, что производная также является функцией, и сечи она дифференци­руема, то от нее, в свою очередь, можно взять производную, которую называют второй производной (или производной второ­го порядка) и обозначают

Производной третьего порядка (или третьей производной) называют производную от второй производной. Ее обозначают

Например, для функции имеем

Вообще, производной п-го порядка от функции _. Называется производная от производной (n—1)-го порядка. Ее обозначают: . Таким образом, производную n-го порядка можно найти последовательным дифференцированием данной функции.

415—422. Найти производные второго порядка заданных функ­ций:

423—432. Найти производные третьего порядка заданных функций:

239

Рассмотрим механический смысл производной второго поряд­ка.

Пусть тело движется прямолинейно по закону . Как

известно, скорость v движения тела в данный момент времени равна производной пути по времени, т. е.

Если тело движется неравномерно, то скорость и с течением времени изменяется и за промежуток времени получает при­ращение v. В этом случае величина отношения , показываю­щая изменение скорости в единицу времени, называется сред­ним ускорением в промежутке времени от до

Пусть ; тогда , а среднее ускорение стремится к величине, которая называется ускорением в данный момент времени t. Следовательно, ускорение движущегося тела представляет собой скорость изменения его скорости.

Обозначив ускорение через а, получим

Таким образом, ускорение прямолинейного движения тела в данный момент равно второй производной пути по времени, вычисленной для данного момента.

В этом и заключается механический смысл второй произ­водной.

433. Точка движется прямолинейно но закону . Найти скорость и ускорение точки в момент t = 4. Решение. Для определения скорости нужно найти первую произвольную данной функции при t =4. Имеем

Ускорение равно второй производной функции при t = 4, т. е.

Величину ускорения оказалась постоянной для любого значения t; значит, движение точки по заданному закону происходит с постоян­ным ускорением.

434. Материальная точка движется по закону . Найти ее ускорение в конце 3-й секунды.

435.В момент времени t тело находится на расстоянии км от места отправления. Найти его ускоре­ние через 2 ч.

240

436. Вычислить ускорение материальной точки в конце 3-й секунды, если точка движется по закону

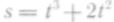
437. Путь, пройденный клетью подъемной машины, определяется уравнением 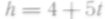. Найти скорость и ускорение в любой момент времени.

438. Определить момент t, в который ускорение прямолиней­ного движения, совершаемого по закону 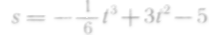, равно нулю. Какова при этом скорость?

439.Закон движения частицы определяется уравнением . Каково ускорение частицы в момент, когда ее ско­рость равна 1 м/с?

440. Точка движется вдоль оси абсцисс по закону , где t-время о секундах, отсчитываемое от t= 0, а

х — расстояние движущейся точки от начала координат в мет­рах. Требуется: а) определить закон изменения скорости и уско­рения движения от времени t; б) найти начальную скорость и скорость в момент t=3 с; в) установить, существуют ли момен­ты времени, когда скорость равна нулю, и если да, то какие положения движущейся точки соответствуют этим моментом

Решение. а) Для определения скорости движения найдем про­изводную пули по времени:

а для определения ускорения движения- производную скорости пи времени:

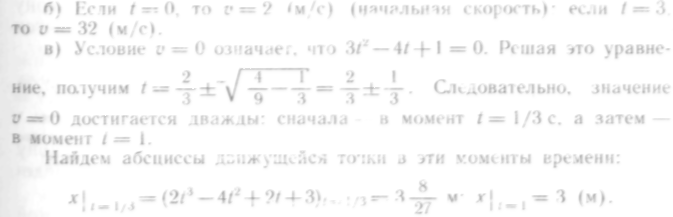
441. Тело, масса которого 30 кг движется прямолинейно по закону . Доказать, что движение тела происходит под действием постоянной силы.

Решение. Имеем _. Следовательно,

, т.е. при данном законе движения тело движется с постоянным ускорением 8 м/с. Далее, так как масса тела постоянна (30 кг), то по второму закону Ньютона действующая на него сила

— также постоянная величина.

241

442.Тело массой 3 кг движется прямолинейно по закону _. Найти силу, действующую на тело в момент времени

443.Показать, что если тело движется по закону _, то его ускорение численно равно пройденному пути.